本节课我们进一步探讨了三角函数各种变换的实质和函数y = Asin(wx+j)(A>0，w>0)的图像的画法。并通过改变各种变换的顺序而发现：平移变换应在周期变换之前，否则得到的函数图像不是函数y =Asin(wx+j)的图像由y = sinx图像的得到。

2. 函数y=Asin(wx+j)(A>0，w>0)图像和函数y=sinx图像的关系。

　　 利用制作好的课件，运用多媒体教学手段向学生展示由函数y=sinx的图像是怎样经过平移变化→周期变换→振幅变换而得到函数y=Asin (wx+j)图像的。四、指导创新

　　 上面我们学习了函数y = Asin(wx+j)的图像可由y = sinx图像平移变换→周期变换→振幅变换的顺序而得到，若按下列顺序得到y = Asin(wx+j)的图象吗？

　　 ⑴周期变换→平移变换→振幅变换

　　 ⑵振幅变换→平移变换→周期变换

　　 ⑶平移变换→振幅变换→周期变换　

　　 教师利用制作好的课件，运用多媒体逐一演示验证，让学生发现规律：若周期变换在前，平移变换在后，则得到的函数图像不是函数y = Asin(wx+j)的图像，振幅变换出现在前或后不会影响得到函数y = Asin(wx+j)的图像。

　　 教师指导学生探讨⑴的变换顺序不能得到函数y = Asin(wx+j) (A>0，w>0)图像的原因，并通过在平移变换过程中的单位变换而调整到函数y = Asin(wx+j)图像的一般公式。

　　 原因：y = sinx　 y =Asinwx

　　 y = sinw(x+j) = sin(wx+wj)y = Asin(wx+wj)

　　 一般公式：将平移变换单位改为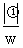：即可。

1. 函数y = Asin(wx+j)的图像的画法。

　　 为了探讨函数y = Asin(wx+j)的图像和函数y = sinx图像的关系，我们先来用“五点法”作函数y = Asin(wx+j)的图像。

　　 例：作函数y = 3sin(2x+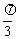)的简图。

　　 解：⑴设Z= 2x +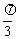，那么3xin(2x+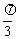)= 3sinZ，x=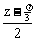=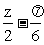，分别取z = 0，，p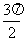，，2p，则得x为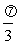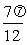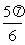，，，，，所对应的五点为函数y=3sin(x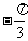)在一个周期[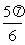，]图象上起关键作用的点。

　　 ⑵列表

x
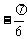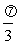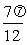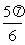2x+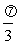	0		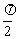p		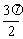2p
sin(2x+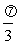)	0	1	0	-1	0
3 sin(2x+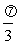)	0	3	0	-3	0

　　 ⑶描点作图，运用制好的课件演示作图过程。(图略)

2. 函数y=Asin(wx+j)(A>0，w>0)图像和函数y=sinx图像的关系。

　　 利用制作好的课件，运用多媒体教学手段向学生展示由函数y=sinx的图像是怎样经过平移变化→周期变换→振幅变换而得到函数y=Asin (wx+j)图像的。

归纳1：先把函数y = sinx的图像上的所有点向左平行移动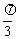个单位，得到y = sin(x³ +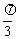)的图像，再把y = sin(x +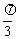)的图像上所有的点的横坐标缩短到原来的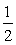倍(纵坐标不变)，得到y = sin(2x +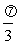)的图像，再把y = sin(2x +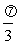)的图像上所有的点的纵坐标伸长到原来的3倍(横坐标不变)，从而得到y = 3sin(2x +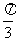)图像。

　　 归纳2：函数y = Asin(wx+j)，(A>0，w>0)的图像可以看作是先把y = sinx的图像上所有的点向左(j>0)或向右(j>1)平移|j|个单位，再把所得各点的横坐标缩短(w>1)或伸长(0<w<1)到原来的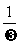倍(纵坐标不变)，再把所得各点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍，(横坐标不变)。即：平移变换→周期变换→振幅变换。三、尝试探究

　　 上面我们学习和复习了三种函数y = sin(x ±k)，y = sinwx，y = Asinx的图像和函数y = sinx图像的关系，那么函数y = Asin(wx+j)(a>0，w>0) 的图像和函数y = sinx的图像有何关系呢？三、尝试探究

1. 函数y = Asin(wx+j)的图像的画法。

　 为了探讨函数y = Asin(wx+j)的图像和函数y = sinx图像的关系，我们先来用“五点法”作函数y = Asin(wx+j)的图像。

　 例：作函数y = 3sin(2x+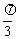)的简图。

　 解：⑴设Z= 2x +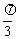，那么3xin(2x+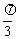)= 3sinZ，x=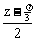=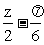，分别取z = 0，，p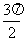，，2p，则得x为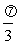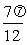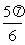，，，，，所对应的五点为函数y=3sin(x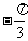)在一个周期[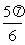，]图象上起关键作用的点。

　　 ⑵列表

x
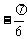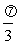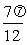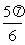2x+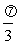	0		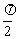p		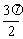2p
sin(2x+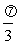)	0	1	0	-1	0
3 sin(2x+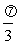)	0	3	0	-3	0

　　 ⑶描点作图，运用制好的课件演示作图过程。(图略)

4. 函数y = Asinx(A>0)的图像和函数y = sinx图像的关系是什么？

　　 学生答：函数y = Asinx的图像可由函数y = sinx的图像沿y轴伸长(A>1)或缩短(x<1)到原来的A倍而得到的，称为振幅变换。

　　 演示：教师利用多媒体，运用制好的课件将变化过程演示给学生看，并要求学生具体观察图像上点坐标的变化，然后归纳出这种变换的实质是：横坐标不变，纵坐标伸长(A> | )或缩小(0<A<1)到原来的A倍。

3. 函数y = sinwx (w>0)的图像和函数y = sinx图像的关系是什么？

　　 学生答：函数y = sinwx(w>0)的图像可由函数y = sinx的图像沿x轴伸长(w<1)或缩短(w>1)到原来的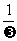倍而得到，称为周期变换。

　　 演示：教师运用多媒体演示变化过程，并要求学生观察图像上点坐标的变化，然后进一步总结这种变化的实质是纵坐标不变，横坐标伸长(0<w<1)或缩短(w>1)到原来的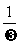倍。

2. 函数y = sin(x±k)(k>0)的图象和函数y = sinx图像的关系是什么？

　　 生答：函数y = sin(x ±k)(k>0)的图像可由函数y = sinx的图像向左(或右)平移k个单位而得到，学生回答后，教师应用多媒体演示变化过程，并要求同学观察图像上点坐标的变化，然后进一步总结出这种变换实际上是纵坐标不变，横坐标增加(或减少)k个单位，这种变换称为平移变换。

1.“五点法”作函数y=sinx简图的步骤，其中“五点”是指什么？

以下函数中，不是奇函数的是(　　 )

A.y＝sinx+tanx　 B．y＝xtanx－1 C．y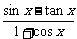＝　 D．y＝lg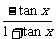

3.下列命题中正确的是(　　 )

A．y＝cosx在第二象限是减函数　 B．y＝tanx在定义域内是增函数

C．y＝｜cos(2x+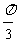)｜的周期是 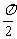D．y＝sin｜x｜是周期为2π的偶函数