2、在确定分段间隔k时应注意：分段间隔k为整数，当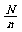不是整数时，应采用等可能剔除的方剔除部分个体，以获得整数间隔k。

[评价设计]

(1)采用随机抽样的方法将总体中的N个个编号。

(2)将整体按编号进行分段，确定分段间隔k(k∈N,L≤k).

(3)在第一段用简单随机抽样确定起始个体的编号L(L∈N,L≤k)。

(4)按照一定的规则抽取样本，通常是将起始编号L加上间隔k得到第2个个体编号L+K，再加上K得到第3个个体编号L+2K，这样继续下去，直到获取整个样本。

[说明]从系统抽样的步骤可以看出，系统抽样是把一个问题划分成若干部分分块解决，从而把复杂问题简单化，体现了数学转化思想。

[例题精析]

　　 例1、某校高中三年级的295名学生已经编号为1，2，……，295，为了了解学生的学习情况，要按1：5的比例抽取一个样本，用系统抽样的方法进行抽取，并写出过程。

[分析]按1：5分段，每段5人，共分59段，每段抽取一人，关键是确定第1段的编号。

解：按照1：5的比例，应该抽取的样本容量为295÷5=59，我们把259名同学分成59组，每组5人，第一组是编号为1-5的5名学生，第2组是编号为6-10的5名学生，依次下去，59组是编号为291-295的5名学生。采用简单随机抽样的方法，从第一组5名学生中抽出一名学生，不妨设编号为k(1≤k≤5)，那么抽取的学生编号为k+5L(L=0,1,2,……，58)，得到59个个体作为样本，如当k=3时的样本编号为3，8，13，……，288，293。

例2、从忆编号为1-50的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射实验，若采用每部分选取的号码间隔一样的系统抽样方法，则所选取5枚导弹的编号可能是

A．5，10，15，20，25　　　　　 B、3，13，23，33，43

C．1，2，3，4，5　　　　　　　 D、2，4，6，16，32

[分析]用系统抽样的方法抽取至的导弹编号应该k,k+d,k+2d,k+3d,k+4d,其中d=50/5=10,k是1到10中用简单随机抽样方法得到的数，因此只有选项B满足要求，故选B。

[课堂练习]P49　 练习1. 2. 3

[课堂小结]

1、在抽样过程中，当总体中个体较多时，可采用系统抽样的方法进行抽样，系统抽样的步骤为：

(1)采用随机的方法将总体中个体编号；

(2)将整体编号进行分段，确定分段间隔k(k∈N)；

(3)在第一段内采用简单随机抽样的方法确定起始个体编号L；

(4)按照事先预定的规则抽取样本。

一般地，要从容量为N的总体中抽取容量为n的样本，可将总体分成均衡的若干部分，然后按照预先制定的规则，从每一部分抽取一个个体，得到所需要的样本，这种抽样的方法叫做系统抽样。

[说明]由系统抽样的定义可知系统抽样有以下特证：

(1)当总体容量N较大时，采用系统抽样。

(2)将总体分成均衡的若干部分指的是将总体分段，分段的间隔要求相等，因此，系统抽样又称等距抽样，这时间隔一般为k＝[].

(3)预先制定的规则指的是：在第1段内采用简单随机抽样确定一个起始编号，在此编号的基础上加上分段间隔的整倍数即为抽样编号。

思考？

　　 (1)你能举几个系统抽样的例子吗？

(2)下列抽样中不是系统抽样的是　　　 (　 )

A、从标有1~15号的15号的15个小球中任选3个作为样本，按从小号到

大号排序，随机确定起点i,以后为i+5, i+10(超过15则从1再数起)号入样

B工厂生产的产品，用传关带将产品送入包装车间前，检验人员从传送带上每隔五分钟抽一件产品检验

C、搞某一市场调查，规定在商场门口随机抽一个人进行询问，直到调查到事先规定的调查人数为止

D、电影院调查观众的某一指标，通知每排(每排人数相等)座位号为14的观众留下来座谈

点拨:(2)c不是系统抽样，因为事先不知道总体，抽样方法不能保证每个个体按事先规定的概率入样。

(五)课后作业

1、判断题：

(1)a∥b　 c⊥a => c⊥b　 (　　 )

(1)a⊥c　 b⊥c => a⊥b　 (　　 )

2、填空题：

在正方体ABCD-A'B'C'D'中，与BD'成异面直线的有 ________ 条。

(四)课堂小结

在师生互动中让学生了解：

(1)本节课学习了哪些知识内容？

(2)计算异面直线所成的角应注意什么？

(三)课堂练习

教材P49 练习1、2

充分调动学生动手的积极性，教师适时给予肯定。

(二)讲授新课

1、教师给出长方体模型，引导学生得出空间的两条直线有如下三种关系：

平行直线：同一平面内，没有公共点；

异面直线：　 不同在任何一个平面内，没有公共点。

教师再次强调异面直线不共面的特点，作图时通常用一个或两个平面衬托，如下图：

2、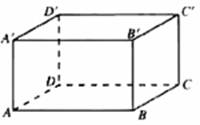(1)师：在同一平面内，如果两条直线都与第三条直线平行，那么这两条直线互相平行。在空间中，是否有类似的规律？

组织学生思考：

长方体ABCD-A'B'C'D'中，

BB'∥AA'，DD'∥AA'，

BB'与DD'平行吗？

生：平行

再联系其他相应实例归纳出公理4

公理4：平行于同一条直线的两条直线互相平行。

符号表示为：设a、b、c是三条直线

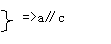a∥b

c∥b

强调：公理4实质上是说平行具有传递性，在平面、空间这个性质都适用。

公理4作用：判断空间两条直线平行的依据。

(2)例2(投影片)

例2的讲解让学生掌握了公理4的运用

(3)教材P47探究

让学生在思考和交流中提升了对公理4的运用能力。

3、组织学生思考教材P47的思考题

(投影)

让学生观察、思考：

∠ADC与A'D'C'、∠ADC与∠A'B'C'的两边分别对应平行，这两组角的大小关系如何？

生：∠ADC = A'D'C'，∠ADC + ∠A'B'C' = 180⁰

教师画出更具一般性的图形，师生共同归纳出如下定理

等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。

教师强调：并非所有关于平面图形的结论都可以推广到空间中来。

4、以教师讲授为主，师生共同交流，导出异面直线所成的角的概念。

(1)师：如图，已知异面直线a、b，经过空间中任一点O作直线a'∥a、b'∥b，我们把a'与b'所成的锐角(或直角)叫异面直线a与b所成的角(夹角)。

(2)强调：

① a'与b'所成的角的大小只由a、b的相互位置来确定，与O的选择无关，为了简便，点O一般取在两直线中的一条上；

② 两条异面直线所成的角θ∈(0，　 )；

③ 当两条异面直线所成的角是直角时，我们就说这两条异面直线互相垂直，记作a⊥b；

④ 两条直线互相垂直，有共面垂直与异面垂直两种情形；

⑤ 计算中，通常把两条异面直线所成的角转化为两条相交直线所成的角。

(3)例3(投影)

例3的给出让学生掌握了如何求异面直线所成的角，从而巩固了所学知识。

(一)创设情景、导入课题

1、通过身边诸多实物，引导学生思考、举例和相互交流得出异面直线的概念：不同在任何一个平面内的两条直线叫做异面直线。

2、师：那么，空间两条直线有多少种位置关系？(板书课题)

2、教学用具：投影仪、投影片、长方体模型、三角板