
3、某中学高一年级有学生600人,高二年级有学生450人,高三年级有学生750人,每个学生被抽到的可能性均为0.2,若该校取一个容量为n的样本,则n= 。
2、某校有500名学生,其中O型血的有200人,A型血的人有125人,B型血的有125人,AB型血的有50人,为了研究血型与色弱的关系,要从中抽取一个20人的样本,按分层抽样,O型血应抽取的人数为 人,A型血应抽取的人数为 人,B型血应抽取的人数为 人,AB型血应抽取的人数为 人。
1、某单位有老年人28人,中年人54人,青年人81人,为了调查他们的身体情况,需从他们中抽取一个容量为36的样本,则适合的抽取方法是 ( )
A.简单随机抽样
B.系统抽样
C.分层抽样
D.先从老人中剔除1人,然后再分层抽样
2、分层抽样的优点是:使样本具有较强的代表性,并且抽样过程中可综合选用各种抽样方法,因此分层抽样是一种实用、操作性强、应用比较广泛的抽样方法。
[评论设计]
(1)分层:按某种特征将总体分成若干部分。
(2)按比例确定每层抽取个体的个数。
(3)各层分别按简单随机抽样的方法抽取。
(4)综合每层抽样,组成样本。
[说明]
(1)分层需遵循不重复、不遗漏的原则。
(2)抽取比例由每层个体占总体的比例确定。
(3)各层抽样按简单随机抽样进行。
探究交流
(1)分层抽样又称类型抽样,即将相似的个体归入一类(层),然后每层抽取若干个体构成样本,所以分层抽样为保证每个个体等可能入样,必须进行 ( )
A、每层等可能抽样
B、每层不等可能抽样
C、所有层按同一抽样比等可能抽样
(2)如果采用分层抽样,从个体数为N的总体中抽取一个容量为n
样本,那么每个个体被抽到的可能性为 ( )
A.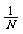 B.
B.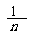 C.
C.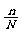 D.
D.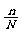
点拨:
(1)保证每个个体等可能入样是简单随机抽样、系统抽样、分层抽
共同的特征,为了保证这一点,分层时用同一抽样比是必不可少的,故此选C。
(2)根据每个个体都等可能入样,所以其可能性本容量与总体容量
比,故此题选C。
知识点2 简单随机抽样、系统抽样、分层抽样的比较
|
类
别 |
共同点 |
各自特点 |
联 系 |
适
用 范 围 |
|
|
简
单 随 机 抽 样 |
(1)抽样过程中每个个体被抽到的可能性相等 (2)每次抽出个体后不再将它放回,即不放回抽样 |
从总体中逐个抽取 |
|
总体个数较少 |
|
|
将总体均分成几部 分,按预先制定的规则在各部分抽取 |
在起始部分 样时采用简 随机抽样 |
总体个数较多 |
|||
|
系
统 抽 样 |
|||||
|
将总体分成几层, 分层进行抽取 |
分层抽样时采用简单随机抽样或系统抽样 |
总体由差异明显的几部分组成 |
|||
|
分
层 抽 样 |
|
[例选精析]
例1、 某高中共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取容量为45的样本,那么高一、高二、高三各年级抽取的人数分别为
A.15,5,25 B.15,15,15
C.10,5,30 D15,10,20
[分析]因为300:200:400=3:2:4,于是将45分成3:2:4的三部分。设三部分各抽取的个体数分别为3x,2x,4x,由3x+2x+4x=45,得x=5,故高一、高二、高三各年级抽取的人数分别为15,10,20,故选D。
例2:一个地区共有5个乡镇,人口3万人,其中人口比例为3:2:5:2:3,从3万人中抽取一个300人的样本,分析某种疾病的发病率,已知这种疾病与不同的地理位置及水土有关,问应采取什么样的方法?并写出具体过程。
[分析]采用分层抽样的方法。
解:因为疾病与地理位置和水土均有关系,所以不同乡镇的发病情况差异明显,因而采用分层抽样的方法,具体过程如下:
(1)将3万人分为5层,其中一个乡镇为一层。
(2)按照样本容量的比例随机抽取各乡镇应抽取的样本。
300×3/15=60(人),300×2/15=100(人),300×2/15=40(人),300×2/15=60(人),因此各乡镇抽取人数分别为60人、40人、100人、40人、60 人。
(3)将300人组到一起,即得到一个样本。
[课堂练习]P52 练习1. 2. 3
[课堂小结]
1、分层抽样是当总体由差异明显的几部分组成时采用的抽样方法,进行分层抽样时应注意以下几点:
(1)、分层抽样中分多少层、如何分层要视具体情况而定,总的原则是,层内样本的差异要小,面层之间的样本差异要大,且互不重叠。
(2)为了保证每个个体等可能入样,所有层应采用同一抽样比等可能抽样。
(3)在每层抽样时,应采用简单随机抽样或系统抽样的方法进行抽样。
一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样的方法叫分层抽样。
[说明]分层抽样又称类型抽样,应用分层抽样应遵循以下要求:
(1)分层:将相似的个体归人一类,即为一层,分层要求每层的各个个体互不交叉,即遵循不重复、不遗漏的原则。
(2)分层抽样为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,每层样本数量与每层个体数量的比与这层个体数量与总体容量的比相等。
(四)作业
1、让学生回去整理这三节课的内容,理清脉络。
2、教材P52 习题2.1 A组第5题
(三)归纳整理、整体认识
教师引导学生归纳,整理本节课的知识脉络,提升他们掌握知识的层次。
(二)研探新知
1、引导学生观察、思考身边的实物,从而直观、准确地归纳出直线与平面有三种位置关系:
(1)直线在平面内 -- 有无数个公共点
(2)直线与平面相交 -- 有且只有一个公共点
(3)直线在平面平行 -- 没有公共点
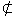 指出:直线与平面相交或平行的情况统称为直线在平面外,可用a α来表示
指出:直线与平面相交或平行的情况统称为直线在平面外,可用a α来表示
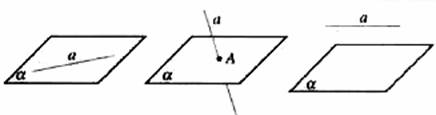
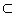 a α
a∩α=A
a∥α
a α
a∩α=A
a∥α
例4(投影)
师生共同完成例4
例4的给出加深了学生对这几种位置关系的理解。
2、引导学生对生活实例以及对长方体模型的观察、思考,准确归纳出两个平面之间有两种位置关系:
(1)两个平面平行 -- 没有公共点
(2)两个平面相交 -- 有且只有一条公共直线
用类比的方法,学生很快地理解与掌握了新内容,这两种位置关系用图形表示为
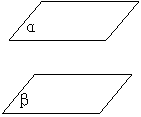
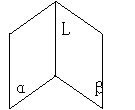
α∥β α∩β= L
教师指出:画两个相互平行的平面时,要注意使表示平面的两个平行四边形的对应边平行。
教材P51 探究
让学生独立思考,稍后教师作指导,加深学生对这两种位置关系的理解
教材P51 练习
学生独立完成后教师检查、指导
(一)创设情景、导入课题
教师以生活中的实例以及课本P49的思考题为载体,提出了:空间中直线与平面有多少种位置关系?(板书课题)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com