1、向量加法的几何意义；

练习：P95

5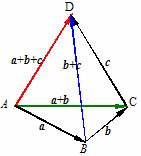．向量加法的结合律：(+) +=+ (+)

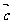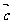证：如图：使， ，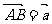

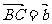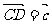
则(+) +=，+ (+) =

∴(+) +=+ (+)

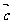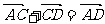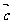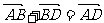
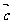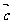从而，多个向量的加法运算可以按照任意的次序、任意的组合来进行.

4．加法的交换律和平行四边形法则

问题：上题中+的结果与+是否相同？　　 验证结果相同

从而得到：1)向量加法的平行四边形法则(对于两个向量共线不适应)

　　　 2)向量加法的交换律：+=+

3．例一、已知向量、，求作向量+

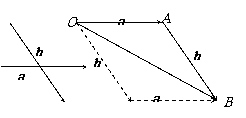
　 作法：在平面内取一点，作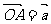 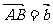，则.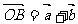

2、三角形法则(“首尾相接，首尾连”)

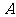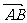如图，已知向量a、b.在平面内任取一点，作＝a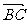，＝b，则向量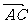叫做a与b的和，记作a+b，即 a+b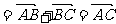，规定：　　　 a + 0-= 0 +

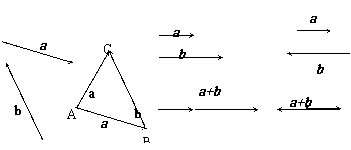
探究：(1)两相向量的和仍是一个向量；

(2)当向量与不共线时，+的方向不同向，且|+|<||+||；

(3)当与同向时，则+、、同向，且|+|=||+||，当与反向时，若||>||，则+的方向与相同，且|+|=||-||；若||<||，则+的方向与相同，且|+b|=||-||.

(4)“向量平移”(自由向量)：使前一个向量的终点为后一个向量的起点，可以推广到n个向量连加

1、向量的加法：求两个向量和的运算，叫做向量的加法.

2、　 情景设置：

(1)某人从A到B，再从B按原方向到C，

　 则两次的位移和：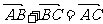

(2)若上题改为从A到B，再从B按反方向到C，

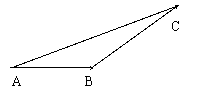　 则两次的位移和：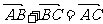

(3)某车从A到B，再从B改变方向到C，

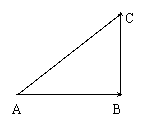　 则两次的位移和：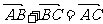

(4)船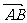速为，水速为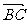，则两速度和：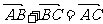

1、　　 复习：向量的定义以及有关概念

强调：向量是既有大小又有方向的量.长度相等、方向相同的向量相等.因此，我们研究的向量是与起点无关的自由向量，即任何向量可以在不改变它的方向和大小的前提下，移到任何位置

4、对某单位1000名职工进行某项专门调查，调查的项目与职工任职年限有关，人事部门提供了如下资料：

试利用上述资料设计一个抽样比为1/10的抽样方法。