
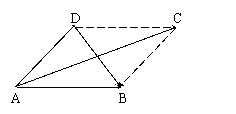
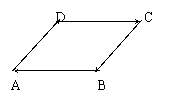
3.如图,在四边形ABCD中,根据图示填空:
a+b= ,b+c= ,c-d= ,a+b+c-d= .
2.O为平行四边形ABCD平面上的点,设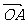 =a,
=a, 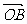 =b,
=b,
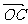 =c,
=c,
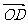 =d,则
=d,则
A.a+b+c+d=0 B.a-b+c-d=0 C.a+b-c-d=0 D.a-b-c+d=0
1.在△ABC中, 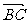 =a,
=a,
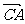 =b,则
=b,则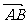 等于( )
等于( )
A.a+b? B.-a+(-b) C.a-b? D.b-a
用a、b表示向量 、
、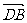 .
.
解:由平行四边形法则得:
 = a + b,
= a + b, 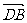 =
=  = a-b
= a-b
变式一:当a, b满足什么条件时,a+b与a-b垂直?(|a| = |b|)
变式二:当a, b满足什么条件时,|a+b| = |a-b|?(a, b互相垂直)
 变式三:a+b与a-b可能是相当向量吗?(不可能,∵ 对角线方向不同)
变式三:a+b与a-b可能是相当向量吗?(不可能,∵ 对角线方向不同)
练习:P98
解:在平面上取一点O,作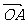 = a,
= a, 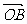 = b,
= b, 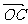 = c,
= c,  = d,
= d,
 作
作 ,
,  , 则
, 则 = a-b,
= a-b,  = c-d
= c-d
4. 探究:
1)如果从向量a的终点指向向量b的终点作向量,那么所得向量是b - a.
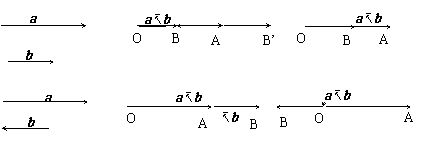
2)若a∥b, 如何作出a - b ?
3. 求作差向量:已知向量a、b,求作向量
∵(a-b) + b = a + (-b) + b = a + 0 = a
作法:在平面内取一点O,
作 = a,
= a, 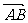 = b
= b
则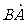 = a - b
= a - b
即a - b可以表示为从向量b的终点指向向量a的终点的向量.
注意:1°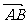 表示a - b.强调:差向量“箭头”指向被减数
表示a - b.强调:差向量“箭头”指向被减数
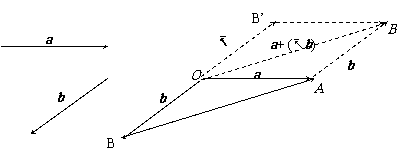 2°用“相反向量”定义法作差向量,a - b = a + (-b)
2°用“相反向量”定义法作差向量,a - b = a + (-b)
显然,此法作图较繁,但最后作图可统一.
2. 用加法的逆运算定义向量的减法:
向量的减法是向量加法的逆运算:
 若b + x = a,则x叫做a与b的差,记作a - b
若b + x = a,则x叫做a与b的差,记作a - b
1. 用“相反向量”定义向量的减法
(1) “相反向量”的定义:与a长度相同、方向相反的向量.记作 -a
(2) 规定:零向量的相反向量仍是零向量.-(-a) = a.
任一向量与它的相反向量的和是零向量.a + (-a) = 0
如果a、b互为相反向量,则a = -b, b = -a, a + b = 0
(3) 向量减法的定义:向量a加上的b相反向量,叫做a与b的差.
即:a - b = a + (-b) 求两个向量差的运算叫做向量的减法.
 向量加法的运算定律:
向量加法的运算定律:
例:在四边形中, .
.
解:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com