
(二)与反三角综合.
例5已知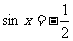 ,根据下列条件求角
,根据下列条件求角 :
:
①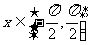 ;②
;②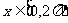 ;③
;③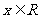
解:①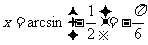 ;
;
②
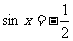 〈0,
〈0,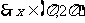 ,
,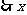 有两个值,
有两个值,
当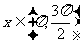 时,
时, ,而
,而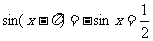 ,
,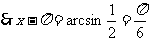 得
得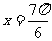
当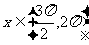 时,
时,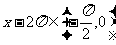 ,而
,而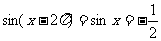 ,
,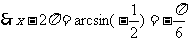 得
得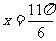 。
。
③从②可知所求为: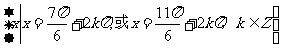
=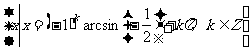
思路点拨:已知三角函数值求在指定区间上的角时先观察是否在可反区间上,若是则直接反即是,若不是则把角变换到可反区间上而由已知求出变换后的角的函数值,然后进行反三角,最后求出所求的角的大小。
(一).与向量综合
例4. ( 05山东)已知向量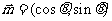 和
和 ,且
,且
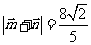 ,求
,求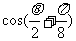 的值
的值
解:
因为


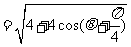
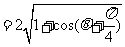
由已知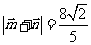 ,得
,得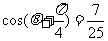

又
所以 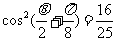

∵ 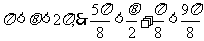 所以
所以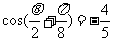
(三).换元思想
例3. P(68)
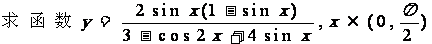 的值域
的值域
(二).整体思想
例2.P(68) 已知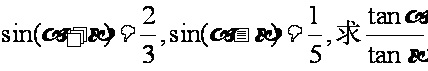 的值.
的值.
思路点拨: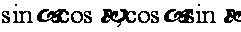 作为整体,或
作为整体,或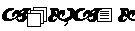 为整体
为整体
深化拓展:P68
(一) 化简思想
例1 (P67).

思路点拨:熟悉三角公式.
4. 三角函数与几何,向量.等关系
3. 三角函数的化简,求值,证明.
2. 三角函数的恒等变形.
1. 三角函数的性质和图象变换;
(1) 求三角函数最值的方法有:①配方法,②化为一个角的三角函数,③数形结合法④换元法,⑤基本不等式法。
(2) 三角函数最值都是在给定区间上取得的,因而要特别注意题设所给出的区间。
(3) 求三角函数的最值时,一般要进行一些三角变换以及代数换元,须注意函数有意义的条件和弦函数的有界性。
(4) 含参数函数的最值,解题要注意参数的作用和影响。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com