
3、注意公式的变形使用,要避免负开方运算,谨慎确定符号。
2、解决三角函数问题一般要做到以下几点:(1)考察角的变化(2)切割化弦(3)平方降次(4)化同为异
1、同角三角函数关系式,诱导公式。
4、三角应用问题三:课堂小结
3、条件求值的题型
例5、已知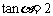 ,求
,求
(1) 的值;
的值;
(2)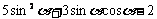 的值。
的值。
解:(1)法一:由已知sinα=2cosα,∴原式=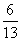 ;
;
法二:∵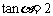 ,∴cosα≠0,∴原式=
,∴cosα≠0,∴原式= =
=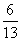 。
。
(2)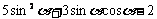 =
=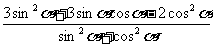 =
=
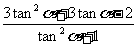 =
=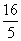
思维点拨:关于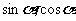 的齐次式的一般处理方法。
的齐次式的一般处理方法。
思考:已知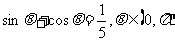 ,求
,求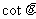 的值。
的值。
解:由已知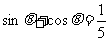 得
得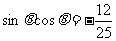 ,所以
,所以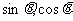 是方程
是方程
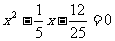 的两根,
的两根,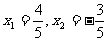
而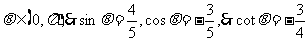
思维点拨:常用关系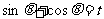 ,则
,则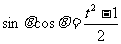 在解题中的作用。
在解题中的作用。
2、证明题
例4)证明:
法一:右边=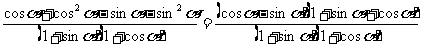
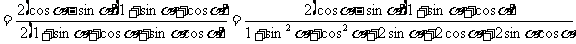
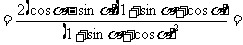 右边
右边
法二:要证等式
即证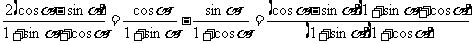
只需证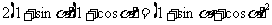
即证
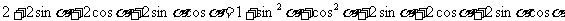 即
即 显然成立
显然成立
所以原等式成立。
思维点拨:证等式常用方法:(1)左边证明到右边或右边证明到左边(从繁到简为原则)
(2)两边向中间证(3)分析法
练习(变式4)求证: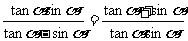
证明:左边=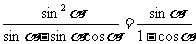
右边=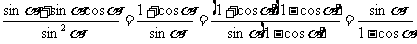
所以原等式成立
思维点拨:“切割化弦”,“化异为同”
1、化简求值
例1:化简(1)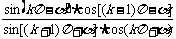 (
(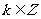 )
)
(2)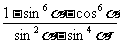
解:(1)当k为偶数时,原式=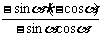 =-1;当k为奇数时同理可得,原式=-1,故当
=-1;当k为奇数时同理可得,原式=-1,故当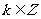 时,原式=-1。
时,原式=-1。
(2)原式=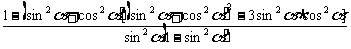 =3
=3
[思维点拨](1)分清k的奇偶,决定函数值符号是关键;
(2)平方降次是化简的重要手段之一。
练习:(变式2)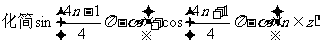
解:原式=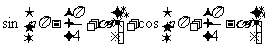
(1)当n为奇数时,设 ,
,
则原式=
=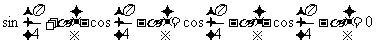 。
。
(2)当n为偶数时,设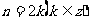 ,同理可得原式=0。
,同理可得原式=0。
例2、(P51)已知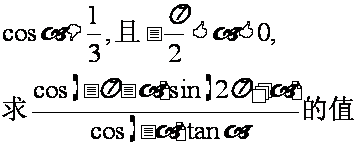
解
思维点拨:先利用诱导公式进行化简,再求值是解题的一般思维。
例3(P52)
(二) 正弦余弦的诱导公式: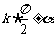
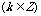 与
与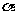 的三角函数关系是“奇变偶不变,符号看象限”。
的三角函数关系是“奇变偶不变,符号看象限”。
注:1、诱导公式的主要作用是将任意角的三角函数转化为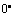 ~
~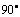 角的三角函数。
角的三角函数。
2、主要用途:
a) 已知一个角的三角函数值,求此角的其他三角函数值(①要注意题设中角的范围,②用三角函数的定义求解会更方便);
b) 化简同角三角函数式;
证明同角的三角恒等式。
(一) 同角三角函数的基本关系式:①平方关系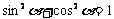 ;②商式关系
;②商式关系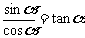 ;③倒数关系
;③倒数关系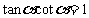 。
。
(三)与函数综合.
(05上海)对定义域是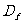 .
.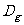 的函数
的函数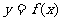 .
. ,
,
规定:函数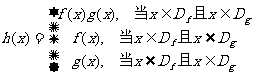
(1)若函数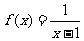 ,
,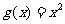 ,写出函数
,写出函数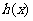 的解析式;
的解析式;
(2)求问题(1)中函数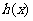 的值域;
的值域;
(3)若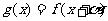 ,其中
,其中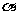 是常数,且
是常数,且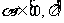 ,请设计一个定义域为R的函数
,请设计一个定义域为R的函数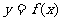 ,及一个
,及一个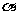 的值,使得
的值,使得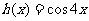 ,并予以证明
,并予以证明
[解] (1)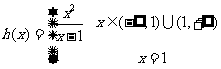
(2) 当x≠1时, h(x)= 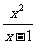 =x-1+
=x-1+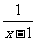 +2,
+2,
若x>1时, 则h(x)≥4,其中等号当x=2时成立
若x<1时, 则h(x)≤ 0,其中等号当x=0时成立
∴函数h(x)的值域是(-∞,0]∪{1}∪[4,+∞)
(3)令 f(x)=sin2x+cos2x,α=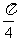
则g(x)=f(x+α)= sin2(x+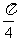 )+cos2(x+
)+cos2(x+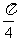 )=cos2x-sin2x,
)=cos2x-sin2x,
于是h(x)= f(x)·f(x+α)= (sin2x+co2sx)( cos2x-sin2x)=cos4x.
另解令f(x)=1+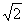 sin2x, α=
sin2x, α=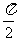 ,
,
g(x)=f(x+α)= 1+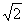 sin2(x+π)=1-
sin2(x+π)=1-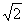 sin2x,
sin2x,
于是h(x)=
f(x)·f(x+α)= (1+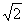 sin2x)( 1-
sin2x)( 1-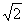 sin2x)=cos4x.
sin2x)=cos4x.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com