1、化简

(1)化简目标：项数习量少，次数尽量低，尽量不含分母和根号

(2)化简三种基本类型：

1)　 根式形式的三角函数式化简

2)　 多项式形式的三角函数式化简

3)　 分式形式的三角函数式化简

(3)化简基本方法：用公式；异角化同角；异名化同名；化切割为弦；特殊值与特殊角的三角函数值互化。

在运用公式时，要注意公式成立的条件，熟练掌握公式的顺用、逆用、变形用，还要注意各种的做题技巧。

(四)综合

例5、(P53例3)

(三).用用边角关系的公式解三角形

例4、(P53例2) 在三角形ABC中,角A..B.C对边a,b,c

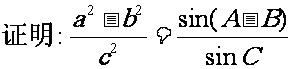
(二),公式逆用

P(53) ( 双基) sin163⁰sin223⁰+sin253⁰sin313⁰

例3　 已知且求

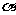分析：涉及与及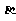的正切和差与积，通常用正切公式的变形公式。

解：原式=

又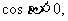所以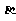为第三象限角，所以

(一)公式正用

例1、求值

(=)

(=)

例2(P53) 设

分析：观察已知角和所求角，可作出，然后利用余弦的倍角公式求解。

解：因为所以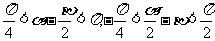

所以，，

所以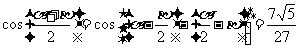

故

(二)倍角公式

注：倍角公式揭示了具有倍数关系的两个角的三角函数的运算规律，可实现函数式的降幂的变化。

注： (1)两角和与差的三角函数公式能够解答的三类基本题型：求值题，化简题，证明题。

(2)对公式会“正用”，“逆用”，“变形使用”。

(3)掌握“角的演变”规律，如

(4)将公式和其它知识衔接起来使用。

(一)两角和与差公式

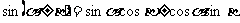
P

4、，，三个式子中，已知其中一个式子的值，求出其余两个式子的值。