y=sinx　　　　　　 y=cosx　　　　　　　 　　　y=tanx 　　　　()

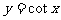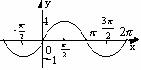
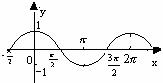
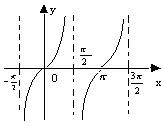
定义域:　 R　　　　　　　 R　　　　　　 　　　

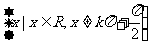
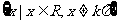
值域:　　 [-1,1]　　　　　　 [-1,1]　　　　　　　　　 R　　　　 　　　　　　R

周期:　 2π　　　　　　　　 2π　　　　　　　　　 π　　　　 　　　　　　π

奇偶性: 奇函数　　　　　 偶函数　　　　　　　　 奇函数　　 　　　　　　奇函数

单调区间:

增区间;;　 　;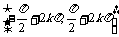　 　　

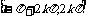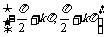
减区间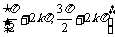;　 　　　　　　　无

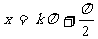
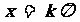对称轴:　　 　　　　　　　无

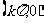
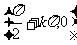
对称中心: 　　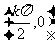　　　　　　　　　　　　　　(以上均)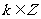

2.重点: 三角函数的值域(最值)、周期、单调区间的求法及未经给出的三角函数的特征研究.

3．三角函数图象的应用

2．图象变换

1．用五点法作图

4．综合

例4．[P59例3]求函数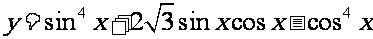

的最小正周期,和最小值;并写出这函数在[0,180⁰]上的单调区间.

预备：某港口水的深度y(米)是时间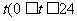，单位：时)的函数，记作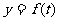，下面是某日水深的数据：

经长期观察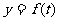，的曲线可以近似地看成函数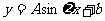的图象。

(1)试根据以上数据，求出函数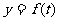的近似表达式，

(2)一般情况下船舶航行时，船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时，船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为6.5米，如果该船希望在同一天内安全进出港，请问，它至多能在港内停留多长时间(忽略进出港所需时间)？

思路分析：由表格写出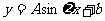解析式。

解：(1)由已知数据，易知函数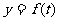的周期T=12，振幅A=3，b=10，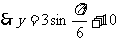

(2)由题意，该船进出港时，水深应不小于5+6.5=11.5米

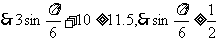,解得: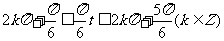

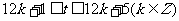,在同一天内,取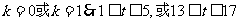

∴该船最早在凌晨1时进港,下午17时出港,在港口内最多停留16个小时.

3．由图象写解析式或由解析式作图

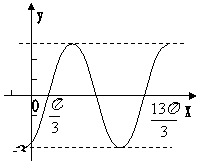
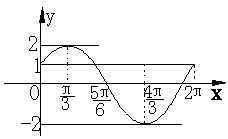
例3如图为某三角函数图象的一段

(1)用正弦函数写出其中一个解析式；

(2)求与这个函数关于直线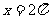对称的函数解析式，并作出它一个周期内简图。

思路分析：由，由最值定A，由特殊值定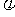，用五点法作简图。

解：(1)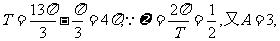

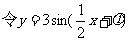由图它过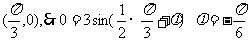(为其中一个值)

(2)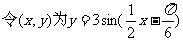上任意一点，该点关于直线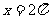对称点为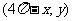

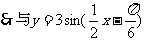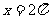关于直线对称的函数解析式是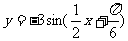

列表：

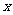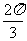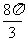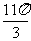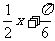	0
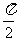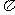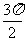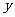	0	-3	0	3	0

作图：

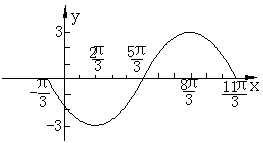
2．三角函数图象的变换

例2．[P58例1]把函数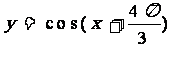 的图象向左平移a个单位,所得到的函数为偶函数,则a 的最小值是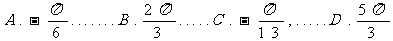

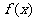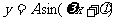思路分析：利用三角变换，将化为求解。

例3.[P59例2]

试述如何由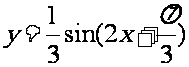的图象得到y=sinx的图象

1．三角函数线的应用

例1：解三角不等式组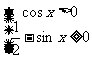

思路分析：利用三角函数线和单调性求解。

解：如图：

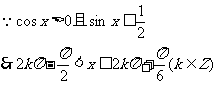
练习：解三角不等式组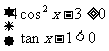

解：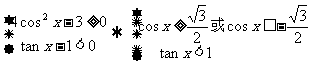

由图得：

4．图象的对称性

①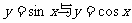的图象既是中心对称图形又是轴对称图形。

②的图象是中心对称图形，有无穷多条垂直于x轴的渐近线。

3．

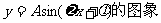
①用五点法作图

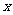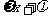	0
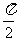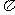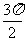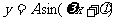	0	A	0	-A	0

②图象变换：平移、伸缩两个程序

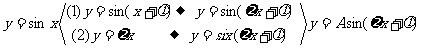
③A---振幅 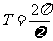----周期　 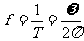----频率