
3、 思维方法:
数形结合,数形转化。
2、 重点、难点:
函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0)的图象、性质。及图象与解析式间的互求。
1、 知识精讲:
⑴一般地,函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0)的图象,可以看作用下面的方法得到:先把正弦曲线上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位长度
(得y=sin(x+φ)图),,再把所得各点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的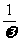 倍(纵坐标不变)(得y=sin(ωx+φ)图,),再把所得各点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变).
倍(纵坐标不变)(得y=sin(ωx+φ)图,),再把所得各点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变).
(若先伸缩,再平移时移多少?)
(2)振幅A、周期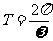 、相位ωx+φ、初相φ。
、相位ωx+φ、初相φ。
(3) y=Asin(ωx+φ)图象的对称轴是: ωx+φ=kπ+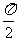 ,即
,即 k∈Z.对称中心为:(
k∈Z.对称中心为:( ,0), k∈Z.
,0), k∈Z.
(4)函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0)的
单调递增区间是:ωx+φ∈[2 kπ-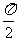 ,2 kπ+
,2 kπ+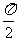 ], k∈Z.
], k∈Z.
单调递减区间是ωx+φ∈[2 kπ+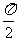 ,2 kπ+
,2 kπ+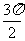 ], k∈Z.
], k∈Z.
(5)y=cos(ωx+φ)也类似。
3.要善于运用图象解题
2.设参 可以帮助理解,熟练了以后可以省却这个过程.
可以帮助理解,熟练了以后可以省却这个过程.
例1[P62]:
判断函数的奇偶性: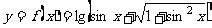
解:定义域为R,且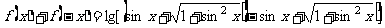
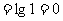
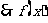 为奇函数.
为奇函数.
练习:(变式)下列命题不正确的是( D )
A、
 是偶函数
B.
是偶函数
B.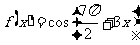 是奇函数
是奇函数
c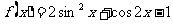 既是奇函数又是偶函数
既是奇函数又是偶函数
D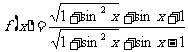 是偶函数。
是偶函数。
例2.P[62]
求下列函数的单调区间. (1).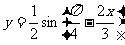 (2).
(2).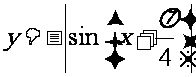
解:(1).原函数变形为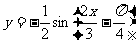 令
令 ,则只需求
,则只需求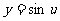 的单调区间即可.
的单调区间即可.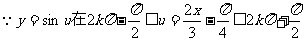 ,(
,(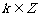 )上
)上
即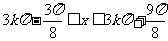 ,(
,(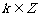 )上单调递增,
)上单调递增,
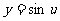 在
在 ,上
,上
即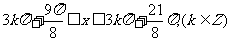 ,上单调递减
,上单调递减
故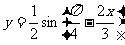 的递减区间为:
的递减区间为: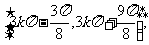 递增区间为:
递增区间为: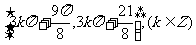 .
.
(2)略
[思维点拔]
例3:[P62]
已知函数
求F(x)的定义域,判断它的奇偶性,并求值域.
例4.( 05浙江)已知函数f(x)=-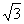 sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ) 求f( )的值; (Ⅱ)
设
)的值; (Ⅱ)
设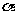 ∈(0,
∈(0,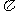 ),f(
),f( )=
)=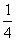 -
-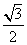 ,求sin
,求sin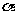 的值.
的值.
. 解:(1)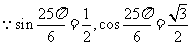 ,
,
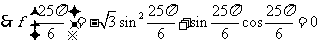

(2)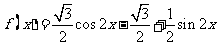

例5.( 05重庆)若函数 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
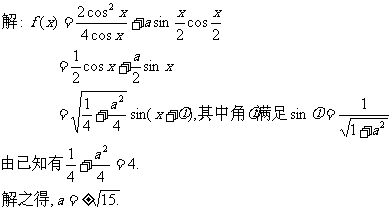
(略)
3.要善于运用图象解题
2.设参 可以帮助理解,熟练了以后可以省却这个过程.
可以帮助理解,熟练了以后可以省却这个过程.
例1[P60]:
(1) 的最大值是?
的最大值是?
(2)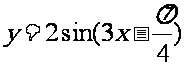 的图象的两条相邻对称轴之间的距离是.
的图象的两条相邻对称轴之间的距离是.
例2.P[60](1)已知f(x)的定义域为[0,1],求f(cosx)的定义域;
(2).求函数y=lgsin(cosx)的定义域
[思维点拔]
例3:[P61]
求函数y=sin6x+cos6x的最小正周期,并求出X为何值时Y有最大值.
例4求下列函数的值域:
(1)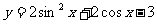 (2)
(2)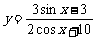
解(1)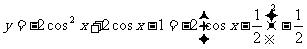

即原函数的值域为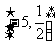
(2)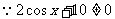
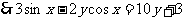
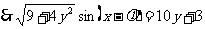 ,其中
,其中 ,由
,由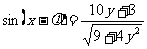 和
和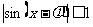
得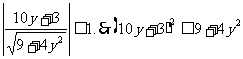 ,
,
整理得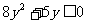 ,所以
,所以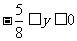
即原函数的值域为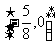
[思维点拔] 前面学过的求函数的值域的方法也适用于三角函数,但应注意三角函数的有界性
.例5:求下列函数的定义域:
1)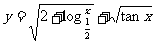 (2)
(2)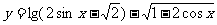
解(1)x应满足 ,即为
,即为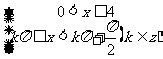
所以所求定义域为
(2)x应满足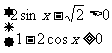 ,利用单位圆中的三角函数线可得
,利用单位圆中的三角函数线可得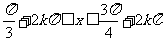
[思维点拔]先转化为三角不等式,可利用单位圆或三角函数的图象进行求解
所以所求定义域为
(备用):已知:函数 (1)求它的定义域和值域. (2)判定它的
(1)求它的定义域和值域. (2)判定它的
奇偶性. (3)求它的单调区间 (4)判定它的周期性,若是周期函数,求它的最小正周期.
解:(1).由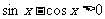

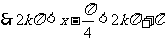
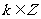
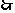 定义域为
定义域为 ,
,

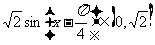
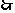 值域为
值域为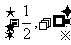
(2). 定义域不关于原点对称,
定义域不关于原点对称,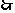 函数为非奇非偶函数
函数为非奇非偶函数
(4).
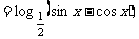
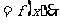 最小正周期T
最小正周期T .
.
[思维点拔] 计算要正确.
备用:已知函数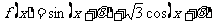 的一条对称轴为Y轴,且
的一条对称轴为Y轴,且 .求
.求 的值.
的值.
解:法一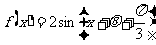 ,令
,令 ,则
,则 ,
,
其对称轴为 ,由题意,
,由题意,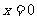 ,
,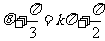 ,
,
即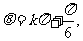


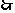 令
令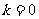 ,得
,得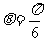
[思维点拔]合一法是个好办法.
法二.由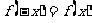 得:
得: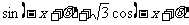

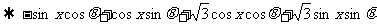
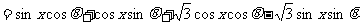
即:
[思维点拔]显然知道三角函数的对称轴,对解题有好处.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com