
1、预测元素的性质(由递变规律推测)
常见的题目给出一种不常见的主族元素(如砹、碲、铋、铅、铟、镭、铯等),或尚未发现的主族元素,推测该元素及其单质或化合物所具有的性质。解答的关键是根据该元素所在族的熟悉的元素的性质,根据递变规律,加以推测判断。
3.元素周期表的应用
|
项 目 |
同周期(从左到右) |
同主族(从上到下) |
|
价电子数 (最外层电子数) |
由1逐渐增到7 |
相同 |
|
主要化合价 |
最高正价由 +1→+7 负价由 -4→-1 |
最高正价相同 |
|
原子半径 |
逐渐减小(惰性气体除外) |
逐渐增大 |
|
金属性与非金属性 |
金属性减弱 非金属性增强 |
金属性增强 非金属性减弱 |
|
最高价氧化物对应水化物的酸碱性 |
碱性减弱 酸性增强 |
碱性增强 酸性减弱 |
|
非金属的气态氢 化物 |
生成由难到易 稳定性由弱到强 |
生成由易到难 稳定性由强到弱 |
|
得失电子能力 |
失电子由 大→小 得电子由 小→大 |
得电子由 大→小 失电子由 小→大 |
原子序数=核电荷数=核内质子数=核外电子数
周期序数=电子层数
主族序数=最外层电子数=元素的最高正价数
*|最高正价数|+|负价数|=8
元素周期表结构的记忆方法如下:
横行叫周期,共有七周期;三四分长短,第七不完全;一八依次现,一零再一遍;
竖行称作族,总共十六族;Ⅷ族最特殊,三行是一族;二三分主副,先主后副;镧锕各十五,均属ⅢB族;构位性一体,相互可推断。
 3个短周期 (1、2、3周期)
3个短周期 (1、2、3周期)
 周期(7个) 3个长周期 (4、5、6周期)
周期(7个) 3个长周期 (4、5、6周期)
1个不完全周期(7周期)
 元素周期表
主族(7个) IA~VIIA
元素周期表
主族(7个) IA~VIIA
副族(7个) IB~VIIB
族(16个) VIII族(1个) 8、9、10三个纵行
零族 (1个) 最右边一个纵行(惰性气体元素)
归纳:七主、七副、一八、一零;三长、三短、一不完全。
3、 研究高次或多个三角函数组合在一起的函数的性质时,一般先将原函数化成
y=Asin(ωx+φ)+b的形式后再研究。
2、由图象求解析式 y=Asin(ωx+φ)+b时一般先确定平衡位置,再确定A,ω的大小,确定φ时要先一点代入。
1、 对于三角函数的变换问题,要注意y=sin(x+φ)→y=sin(ωx+φ)与
y=sinωx→y=sin(ωx+φ)的区别,不同名的要先化为同名。
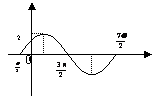 [例1]P64(2003年春季高考·上海)已知函数
[例1]P64(2003年春季高考·上海)已知函数
f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0)
在一个周期内的图象如图所示。求直线y=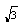
与函数f(x)图象的所有交点的坐标
.[解]根据图象得A=2,T=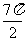 -
-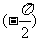 =4π,ω=
=4π,ω=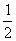
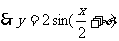 ,又由图象可得相位移为
,又由图象可得相位移为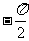 ,
,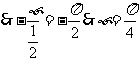 .
.
即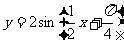 ,根据条件:
,根据条件:
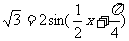 ,
,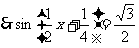
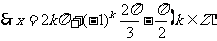
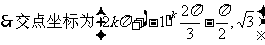
[思维点]按图可求得f(x)=Asin(ωx+φ),再求交点即可。
练习1:写出下列函数图象的解析式
(1)将函数y=sinx的图象上所有点向左平移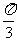 个单位,再把所得图象上各点的横坐标扩大为原来的2倍,得到所求函数的图象。
个单位,再把所得图象上各点的横坐标扩大为原来的2倍,得到所求函数的图象。
(2)将函数y=cosx的图象上所有点横坐标缩为原来的一半,纵坐标保持不变,然后把图象向左平移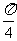 个单位,得到所求函数的图象。
个单位,得到所求函数的图象。
(1)分析:按图象变换的顺序,自变量x的改变量依次是:+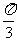 ;
;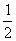 倍。图象的解析式依次为: y=sinx→y=sin(x+
倍。图象的解析式依次为: y=sinx→y=sin(x+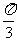 )→y=sin(
)→y=sin(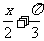 ).
).
解:所求函数图象的解析式为y=sin(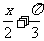 ),也可以写为:y=sin
),也可以写为:y=sin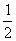 (x+
(x+ ).
).
(2)分析:按图象变换的顺序,自变量x的改变量依次是:2倍;+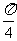 。图象的解析式依次为:y=cosx→y=cos2x→y=cos2(x+
。图象的解析式依次为:y=cosx→y=cos2x→y=cos2(x+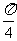 ).
).
解:所求函数图象的解析式为y=cos2(x+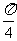 )也可以写为:y=cos(2x+
)也可以写为:y=cos(2x+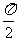 )。
)。
[思维点拨]此类问题关键是A、ω、φ对图形变换的作用。
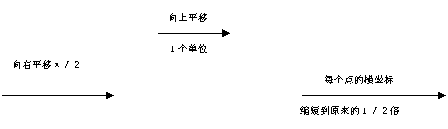 练习2:若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,然后将整个图形沿x轴向左平移
练习2:若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,然后将整个图形沿x轴向左平移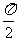 个单位,沿y轴向下平移1个单位,得到曲线与
个单位,沿y轴向下平移1个单位,得到曲线与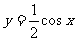 的图象相同,求f(x)的表达式(说明具体过程)
的图象相同,求f(x)的表达式(说明具体过程)
[解]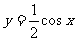
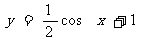
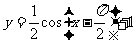
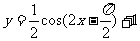
[思维点拨]本题要注意的是图形变换也是互逆的,
 但要注意移的方向。
但要注意移的方向。
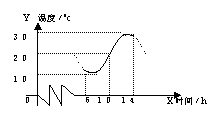
[例2](P62)(2002年高考.全国文史类)如图某地
一天从6时至14时的温度变化曲线近似满足
函数y=Asin(ωx+φ)+b
(1) 求这段时间的最大温差.
(2) 写出这段曲线的函数解析式.
[解](1)由图示,这段时间内的最大温差是30-10=20(0C)
(2)图中从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图
象、
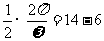 ,
,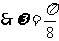 ,由图示A=(30-10)/2=10,b=(30+10)/2=20,
,由图示A=(30-10)/2=10,b=(30+10)/2=20,
这时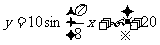 ,将点(6,10)代入上式,可取
,将点(6,10)代入上式,可取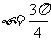
综上所求的解析式为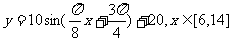
[思维点拨]本题虽是实际问题,但实质还是y=Asin(ωx+φ)+b由图得解析式问题。
例3 P64
函数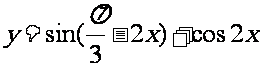 的最小正周期是-------
的最小正周期是-------
练习:已知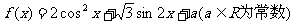
(1) 若x∈R,求f(x)的单调递增区间;
(2)
若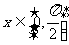 时,f(x)的最大值为4,求
时,f(x)的最大值为4,求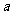 的值
的值
[解](1)由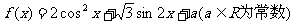
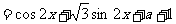
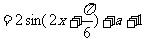 使
使
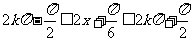 ,解得
,解得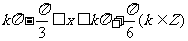 ,
,

(2)由f(x)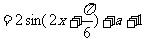 ,因此f(x)在
,因此f(x)在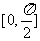 上的最大值为
上的最大值为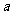 +3,使
+3,使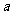 +3=4,
+3=4, 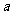 =1.
=1.
例4: .( 05全国(1))设函数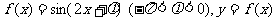 图像的一条对称轴是直线
图像的一条对称轴是直线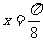

(Ⅰ)求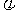 ;
;
(Ⅱ)求函数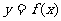 的单调增区间;
的单调增区间;
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,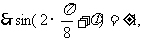
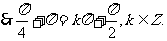
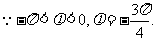
(Ⅱ)由(Ⅰ)知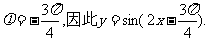
由题意得
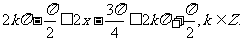
所以函数
[思维点拨]利用三角函数的性质。
4、 特别提示:
y=Asin(ωx+φ),x∈R(其中A>0,ω>0)中A、ω、φ对图形变换的作用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com