1．有机物化学式的确定

(1)“单位物质的量”法

根据有机物的摩尔质量(或相对分子质量)和有机物中各元素的质量分数(或质量比)，求算出1 mol该有机物中各元素原子的物质的量，从而确定分子中的各原子个数来确定有机物的分子式。

(2)最简式法(实验式法)

先求出有机物中各元素原子个数比，然后根据该有机物的摩尔质量或相对原子质量求出分子式。

(3)燃烧通式法

(4)商余法(只适用于烃的分子式的求法)21世纪教育网

根据烷烃(C_nH_2n+2)、烯烃和环烷烃(C_nH_2n)、炔烃和二烯烃(C_nH_2n-2)、苯和苯的同系物(C_nH_2n-6)分子中都有一个共同部分，这部分的相对分子质量为14n。因此用烃的相对分子质量除以14就可以得到分子所含的碳原子数n的值，再根据余数就可以求出烃的分子式。其规律为：

①M/14能除尽，可推知为烯烃或环烷烃，其商为碳原子数。

②M/14余数为2，可推知为烷烃，其商为碳原子数, 氢原子数为2n+2。

③M/14差2能除尽，可推知为炔烃或二烯烃，其商为碳原子数。

④M/14差6能除尽，可推知为苯或苯的同系物，其商为碳原子数。

(5)守恒法

利用反应前后参加反应物质的各元素原子跟反应后生成物的各元素原子守恒，求出有机物的分子式21世纪教育网

(6)讨论法

当反应物的相对用量不确定或条件不足时应根据有机物分子中的碳原子、氢原子要符合化合价组成原则或某种特定性质要求，加上C、H原子数要为正整数，然后进行讨论来确定有机物的分子式21世纪教育网

4. 溶液质量分数与物质的量浓度对应规律

对于某一溶液,溶质质量分数一定时,溶质物质的量浓度、溶液密度也一定，且三者之间存在着对应的转化关系式为：c=ρw/M 。

若以W₁、W₂分别表示浓度为a　 mol/L、b mol/L的某溶液的质量分数，且知a=kb，则W₁=kW₂吗？

利用质量分数和物质的量浓度转换公式c=ρw/M，设溶液密度分别为ρ_a、ρ_b，所以

W₁:W₂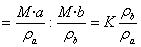

ⅰ)当ρ_a>ρ_b时，W₁>kW₂

ⅱ)当ρ_a<ρ_b时，W₁<kW₂

3. 浓溶液稀释加水的体积

例1. 　 一质量为m克的质量分数为W₁的某溶液加入一定量的水稀释为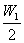的溶液，则加入水的体积为　　　

分析：设加水的质量为x g，根据稀释定律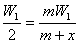： 即x=m，又由于水的密度ρ=1，所以加入水的体积为m mL。

例2. 　在质量为m克物质的量浓度为C₁的某溶液加入一定量的水稀释到物质的量浓度为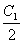，则加入水的体积为　　　

同第二种情形一样，引进密度ρ这一物理量，设加水的体积为V_x,

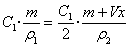　即

当ρ₁>ρ₂时，V_X<m

当ρ₁<ρ₂时，V_X>m

2. 溶液等体积混合的规律

将溶质质量分数分别为W₁、W₂的同种溶液各取V升即等体积混合，混合后的溶液容质质量分数W₃为　　　　

在这里讨论之前必须引进另一个物理量：溶液的密度(ρ)分别设为ρ₁、ρ₂，而且我们还有一个准备工作那就是大多数溶液浓度与密度的变化呈同一方向移动且ρ>1，如硫酸溶液、NaCl溶液等；也存在这样少数溶液其密度与质量分数呈反方向变化且ρ<1，如酒精溶液、氨水溶液等21世纪教育网

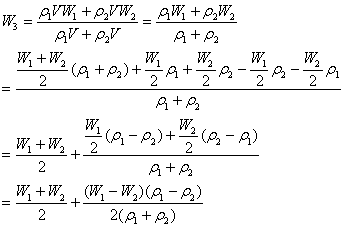
结论：(1)当浓度越大其密度越大的同溶质不同浓度的水溶液等体积相混(ρ>1)，所得混合后的溶液溶质的质量分数大于混合前的两溶液溶质质量分数的平均值。

(2)当浓度越大其密度越小的同溶质不同浓度的水溶液等体积相混(ρ<1)，所得混合后的溶液溶质的质量分数小于混合前的两溶液溶质质量分数的平均值。

1. 溶液等质量混合的规律

将溶质质量分数分别为W₁、W₂的同种溶液各取m克混合，混合后的溶液溶质质量分数W₃为　　　

根据溶质质量分数基本概念W₃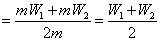，也即不同质量分数的同种溶液等质量混合后的溶液溶质质量分数为其算术平均值。这种情形稍较简单。

3．浓溶液稀释后的pH计算

(1)强酸溶液稀释10倍，其pH增大一个单位。

如果强酸的浓度接近于10^-7mol/L时，无论稀释多少倍，其pH只能是接近于7，但要小于7而显酸性。

(2)强碱溶液稀释100，其pH减小2个单位。

同理，如果强碱溶液中的[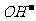]≤10^-8mol/L时，则无论稀释多少倍，其pH只能接近于7但要大于7而显碱性。

2．一定体积不同pH值溶液混合，若二者为强酸，则求出混合溶液的[H⁺]，求pH值；若二者为强碱，则必须求出混合后溶液的[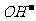]值再化为pH值。若一强酸与一强碱,则求出H⁺离子或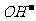离子后,求得[H⁺]化为pH值或求[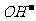]再化为pH值。

1．pH＝－lg[H⁺]，pOH＝－lg[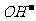]，pH+pOH＝14

aA(g)+bB(g) 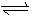cC(g)+dD(g)

盖斯定律在科学研究中具有重要意义。因为有些反应进行的很慢，有些反应不容易直接发生，有些反应的产品不纯(有副反应发生)，这给测定反应热造成了困难。此时如果应用盖斯定律，就可以间接的把它们的反应热计算出来。

例如：C(S)+0.5O₂(g)=CO(g)

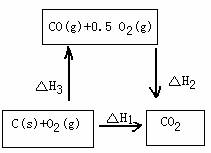　　 上述反应在O₂供应充分时，可燃烧生成CO₂、O₂供应不充分时，虽可生成CO，但同时还部分生成CO₂。因此该反应的△H无法直接测得。但是下述两个反应的△H却可以直接测得：C(_S)+O₂(g)=CO2(g) ； △H₁= - 393.5kJ/mol

CO(g) +0.5 O₂(g)＝CO₂(g) ；△H₂＝ - 283.0kJ/mol

根据盖斯定律，就可以计算出欲求反应的△H3。

分析上述反应的关系，即知

　 △H₁＝△H₂+△H₃

　 △H₃＝△H₁－△H₂＝-393.5kJ/mol­－(-283.0kJ/mol)

　　　　　　　　　　 ＝-110.5kJ/mol