
1.椭圆定义是解决问题的出发点,要明确参数a,b,c,,e的相互关系,几何意义与一些概念的联系.尤其是第二定义,如果运用恰当,可收到事半功倍的效果(如关于求焦半径的问题).
例1:(1) 已知椭圆的对称轴是坐标轴,O为坐标原点,F是一个焦点,A是一个顶点,若椭圆的长轴长是6,且cos∠OFA=2/3。则椭圆方程为________________。
(2) 设椭圆 上的点P到右准线的距离为10,那么点P到左焦点的距离等于_______。
(3) 已知F1为椭圆的左焦点,A,B分别为椭圆的右顶点与上顶点,P为椭圆上的点,当PF1⊥F1A,PO∥AB(O为椭圆中心)时,椭圆的离心率e=_______。(教材P 页例1)。
(4)已知椭圆 上的点P到左焦点的距离等于到右焦点的距离的两倍,则P的坐标是_________。
解:(1) ∵椭圆的长轴长是6,且cos∠OFA=2/3,∴点A不是长轴的端点。∴|OF|=c,|AF|=a=3,∴c=2,b2=5。∴椭圆方程是 ,或 。
(2)由椭圆的第二定义得:点P到左焦点的距离等于12。
(3) 设椭圆方程为 (a>b>0), , F1(-c,0),则点 ,由PO∥AB得kAB=kOP即 ,∴b=c,故 。
(4)设P(x,y),F1,F2分别为椭圆的左右焦点。由已知椭圆的准线方程为 ,
故 ,∵|PF1|=2|PF2|,∴ ,故 。
[思维点拨]1)求离心率一般是先得到a,b,c的一个关系式,然后再求e; 2)由椭圆的一个短轴端点,一个焦点,中心O为顶点组成的直角三角形在求解椭圆问题中经常用到;(3)结合椭圆的第二定义,熟练运用焦半径公式是解决第(3)小题的关键。
例2:如图,设E: (a>b>0)的焦点为 与 ,且 。求证: 的面积 。(图见教材P119页例2的图)
证明:设 ,则 ,
由余弦定理有 =
这样即有
[思维点拨:解与 有关的问题,常用正弦定理或余弦定理,并结合 来解决。
例3:若中心在原点,对称轴为坐标轴的椭圆与直线x+y=1交于A、B两点,M为AB的中点,直线OM(O为原点)的斜率为 ,且OA⊥OB,求椭圆的方程。
解:设椭圆方程为ax2+by2=1,A(x1,y1),B(x2,y2),M( ).
由 消去y得 .
∴ =1- ,
∴ ,∴由 得 ……①; 又OA⊥OB,∴x1x2+y1y2=0,即
x1x2+(1-x1)(1-x2)=0,2x1x2-(x1+x2)+1=0,∴ , ∴a+b=2……②.
联立①②得 ∴方程为 .
[思维点拨]“OA⊥OB x1x2+y1y2=0”(其中A(x1,y1),B(x2,y2))是我们经常用到的一个结论.
例4:(备用)已知椭圆的焦点是F1(-1,0),F2(1,0),P为椭圆上的一点,且|F1F2|是|PF1|和|PF2|的等差中项。(1)求椭圆方程; (2)若点P在第三象限,且∠P F1F2=1200,求tan∠F1PF2。
解:(1)由题设2|F1F2|=|PF1|+|PF2|,c=1。∴2a=4,∴b= 。∴椭圆方程为 。
(2)设∠F1PF2=θ,则∠PF2 F1=600-θ,由正弦定理并结合等比定理可得到
,
∴化简可得 ,∴ ,
从而可求得tan∠F1PF2= 。
[思维点拨]解与△P F1F2有关的问题(P为椭圆上的点)常用正弦定理或余弦定理,并且结合|PF1|+|PF2|=2a来求解。
例5:(备用)(1)已知点P的坐标是(-1,3),F是椭圆 的右焦点,点Q在椭圆上移动,当 取最小值时,求点Q的坐标,并求出其最小值。
(2)设椭圆的中心是坐标原点,长轴在x轴上,离心率为 ,已知点P 这
个椭圆上的点的最远距离是 ,求这个椭圆的方程,并求椭圆上到点P的距离是
的点的坐标。
解(1)由椭圆方程可知a=4,b= ,则c=2, ,
椭圆的右准线方程为x=8 过点Q作QQ’ 于点Q’,
过点P作PP’ 于点P’,则据椭圆的第二定义知,
,
易知当P、Q、Q’在同一条线上时,即当Q’与P’点重合时, 才能取得最小值,最小值为8-(-1)=9,此时点Q的纵坐标为-3,代入椭圆方程得 。
因此,当Q点运动到(2,-3)处时, 取最小值9.
(2)设所求的椭圆的直角坐标方程是
由 ,解得 ,设椭圆上的点(x,y)到点P的距离为d
则
其中 ,如果 , 则当y=-b时,d2取得最大值
解得b= 与 矛盾, 故必有 当 时d2取得最大值, 解得b=1,a=2 所求椭圆方程为
由 可得椭圆上到点P的距离等于 的点为 ,
6.特别注意:椭圆方程中的a,b,c,e与坐标系无关,而焦点坐标,准线方程,顶点坐标,与坐 标系有关.因此确定椭圆方程需要三个条件:两个定形条件a,b,一个定位条件焦点坐标或准线方程.
5.思维方式:待定系数法与轨迹方程法。
4.重难点:椭圆的定义、标准方程和椭圆的简单的几何性质。
1 椭圆的两种定义:
①平面内与两定点F1,F2的距离的和等于定长 的点的轨迹,即点集M={P| |PF1|+|PF2|=2a,2a>|F1F2|};( 时为线段 , 无轨迹)。其中两定点F1,F2叫焦点,定点间的距离叫焦距。
②平面内一动点到一个定点和一定直线的距离的比是小于1的正常数的点的轨迹,即点集M={P| ,0<e<1的常数 。( 为抛物线; 为双曲线)
2 标准方程:(1)焦点在x轴上,中心在原点: (a>b>0);
焦点F1(-c,0), F2(c,0)。其中 (一个 )
(2)焦点在y轴上,中心在原点: (a>b>0);
焦点F1(0,-c),F2(0,c)。其中
注意:①在两种标准方程中,总有a>b>0, 并且椭圆的焦点总在长轴上;
②两种标准方程可用一般形式表示:Ax2+By2=1 (A>0,B>0,A≠B),当A<B时,椭圆的焦点在x轴上,A>B时焦点在y轴上。
3.性质:对于焦点在x轴上,中心在原点: (a>b>0)有以下性质:
坐标系下的性质:
① 范围:|x|≤a,|y|≤b;
② 对称性:对称轴方程为x=0,y=0,对称中心为O(0,0);
③ 顶点:A1(-a,0),A2(a,0),B1(0,-b),B2(0,b),长轴|A1A2|=2a,短轴|B1B2|=2b;( 半长轴长, 半短轴长);
④ 准线方程: ;或
⑤ 焦半径公式:P(x0,y0)为椭圆上任一点。|PF1|= =a+ex0,|PF2|= =a-ex0;|PF1|= =a+ey0,|PF2|= =a-ey0;
平面几何性质:
⑥ 离心率:e= (焦距与长轴长之比) ; 越大越扁, 是圆。
⑦ 焦准距 ;准线间距
⑧ 两个最大角
焦点在y轴上,中心在原点: (a>b>0)的性质可类似的给出(请课后完成)。
22.(本小题满分12分)运货卡车以每小时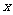 千米的速度匀速行驶130千米路程, 按 交通法规限制
千米的速度匀速行驶130千米路程, 按 交通法规限制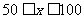 (单位: 千米/小时). 假设汽油的价格是每升2元, 而汽车每小时耗油
(单位: 千米/小时). 假设汽油的价格是每升2元, 而汽车每小时耗油 升, 司机的工资是每小时14元.
升, 司机的工资是每小时14元.
(1)求这次行车总费用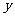 关于
关于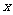 的表达式;
的表达式;
(2)当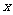 为何值时, 这次行车的总费用最低, 并求出最低费用的值(精确到小数点后 两位,
为何值时, 这次行车的总费用最低, 并求出最低费用的值(精确到小数点后 两位,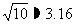 ).
).
21. (本小题满分13分)已知函数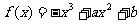 (
(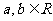 ).
).

(1)若函数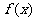 在
在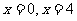 处取得极值,且极小值为
处取得极值,且极小值为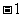 ,求
,求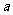 、
、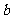 的值;
的值;

(2)若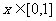 ,函数
,函数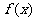 图象上的任意一点的切线斜率为
图象上的任意一点的切线斜率为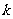 ,求
,求 恒成立时
恒成立时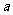 的取值范围.
的取值范围.

20.(本小题满分13分)设数列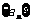 前
前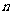 项和为
项和为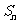 ,且
,且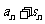 =1(
=1(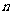
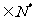 )
)

(1)求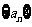 的通项公式;
的通项公式;

(2) 满足
满足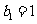 且
且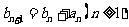 ,求
,求 的通项公式。
的通项公式。

(2) 设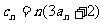 ,求数列
,求数列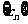 的前
的前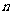 项和
项和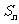


















19.(本小题满分12分)已知向量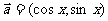 ,
, 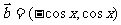 ,
, 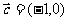 .
.

(1)若 的夹角;
的夹角;

(2)当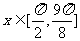 时,求函数
时,求函数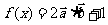 的最大值。
的最大值。













湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com