3．关于太阳活动的叙述正确的是　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．太阳黑子出现在色球层　　 B．太阳活动的周期大约为21年

C．太阳活动强烈会产生磁暴、极光、干扰无线电短波通讯等

D．目前人类生产、生活所需的能源主要来源于太阳活动

太阳是我们的家园，月球围绕地球旋转，我们的地球在离太阳很近的第三条轨道上运行，它处地一个独天得厚的位置上。据此完成1-2小题。

1．上述材料中讲到的天体系统层次共有　　　　　　　　　　　　　　　　　　 (　　 )

A．一个　　　　 B．两个　　　　 C．三个　　　 D．四个

2．这里的“得天独厚的位置”是指　　　　　　　　　　　 　　　　　　　　　(　　 )

A．日地距离适中　　　　　　　　 B．地球自转周期适中　

C．地球质量、体积适中　　　　　 D．大气层的存在

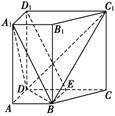
12．(2009·湖南，18)如图，在正三棱柱ABC－A₁B₁C₁中，AB＝AA₁，点D是A₁B₁的中点，点E在A₁C₁上，且DE⊥AE.

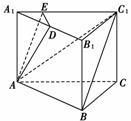
(1)证明：平面ADE⊥平面ACC₁A₁；

(2)求直线AD和平面ABC₁所成角的正弦值．

(1)[证明]　如图所示，由正三棱柱ABC－A₁B₁C₁的性质知AA₁⊥平面A₁B₁C₁.又DE⊂平面A₁B₁C₁，所以DE⊥AA₁.而DE⊥AE，AA₁∩AE＝A.

所以DE⊥平面ACC₁A₁，又DE⊂平面ADE，

故平面ADE⊥平面ACC₁A₁，

(2)[解]　解法一：如图所示，设F是AB的中点，连接DF，DC₁，C₁F，由正三棱柱ABC－A₁B₁C₁的性质及D是A₁B₁的中点知，A₁B₁⊥C₁D，A₁B₁⊥DF，

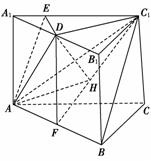
又C₁D∩DF＝D，所以A₁B₁⊥平面C₁DF，而AB∥A₁B₁，所以AB⊥平面C₁DF，又AB⊂平面ABC₁，故平面ABC₁⊥平面C₁DF.

过点D作DH垂直C₁F于H点，则DH⊥平面ABC₁，连接AH，则∠HAD是直线AD和平面ABC₁所成的角．由已知AB＝AA₁，

不妨设AA₁＝，则AB＝2，DF＝，DC₁＝，

C₁F＝，AD＝＝，

DH＝＝＝.

所以sin∠HAD＝＝.

即直线AD和平面ABC₁所成角的正弦值为.

解法二：如图所示，设O是AC的中点，以O为原点建立空间直角坐标系，不妨设AA₁＝，则AB＝2，相关各点的坐标分别是

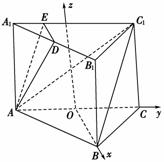
A(0，－1,0)，B(，0,0)，C₁(0,1，)，D(，－，)

易知＝(，1,0)，＝(0,2，)，＝(，，)．

设平面ABC₁的一个法向量为n＝(x，y，z)，则有

解得x＝－y，z＝－y.

故可取n＝(1，－，)．

所以cos〈n·〉＝＝＝.

由此即知直线AD和平面ABC₁所在的角的正弦值为.

亲爱的同学请写上你的学习心得

________________________________________________________________________

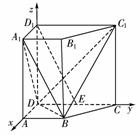
11．(2007·山东)如图所示，在直四棱柱ABCD－A₁B₁C₁D₁中，已知DC＝DD₁＝2AD＝2AB，AD⊥DC，AB∥DC.

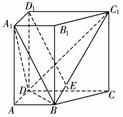
(1)设E是DC的中点，求证：D₁E∥平面A₁BD；

(2)求二面角A₁－BD－C₁的余弦值．

方法一：(1)[证明]　如图连接BE，则四边形DABE为正方形，

∴BE＝AD＝A₁D₁，且BE∥AD∥A₁D₁，

∴四边形A₁D₁EB为平行四边形．

∴D₁E∥A₁B.

又D₁E⊄平面A₁BD，A₁B⊂平面A₁BD，

∴D₁E∥平面A₁BD.

(2)[解]　以D为原点，DA、DC、DD₁所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系，不妨设DA＝1，则D(0,0,0)，A(1,0,0)，B(1,1,0)，C₁(0,2,2)，A₁(1,0,2)，

∴＝(1,0,2)，＝(1,1,0)．

设n＝(x，y，z)为平面A₁BD的一个法向量，由n⊥，n⊥，

得

取z＝1，则n＝(－2,2,1)．

又＝(0,2,2)，＝(1,1,0)．

设m＝(x₁，y₁，z₁)为平面C₁BD的一个法向量，

由m⊥，m⊥，

得

取z₁＝1，则m＝(1，－1,1)．

设m与n的夹角为α，二面角A₁－BD－C₁为π－α，

cosα＝＝＝－

∴cos(π－α)＝－cos α＝，

即所求二面角A₁－BD－C₁的余弦值为.

方法二：(1)[证明]　以D为原点，DA、DC、DD₁所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系，

设DA＝a，由题意知

D(0,0,0)，A(a,0,0)，B(a，a,0)，C(0,2a,0)，C₁(0,2a,2a)，A₁(a,0,2a)，D₁(0,0,2a)，E(0，a,0)

∴＝(0，a，－2a)，＝(0，a，－2a)，

又∵＝，

∴D₁E∥A₁B.

∵A₁B⊂平面A₁BD，D₁E⊄平面A₁BD，

∴D₁E∥平面A₁BD.

(2)[解]　取DB的中点F，DC₁的中点M，连接A₁F、FM，由(1)及题意得知：

F，M(0，a，a)，

∴＝，＝，

＝(a，a,0)．

·＝(，－，2a)·(a，a,0)＝0

·＝·(a，a,0)＝0.

∴FA₁⊥DB，FM⊥DB.

∴∠A₁FM为所求二面角的平面角．

cos∠A₁FM＝

＝

＝＝.

∴二面角A₁－BD－C₁的余弦值为.

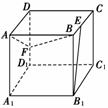
10．如图，正方体ABCD－A₁B₁C₁D₁的棱长为1，E、F分别是棱BC、DD₁上的点，如果B₁E⊥平面ABF，则CE与DF的和的值等于________．

[解析]　以D₁A₁、D₁C₁、D₁D分别为x、y、z轴建立空间直角坐标系，设CE＝x，DF＝y，

则易知E(x,1,1)，B₁(1,1,0)⇒＝(x－1,0,1)，

又F(0,0,1－y)，B(1,1,1)⇒＝(1,1，y)，

由于AB⊥B₁E，故若B₁E⊥平面ABF，

只需·＝(1,1，y)·(x－1,0,1)＝0⇒x+y＝1.

[答案]　1

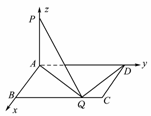
9．如图所示，已知矩形ABCD，AB＝1，BC＝a，PA⊥平面ABCD，若在BC上只有一个点Q满足PQ⊥QD，则a的值等于________．

[解析]　以A为原点，AB、AD、AP所在直线分别为x轴、y轴，z轴建立空间直角坐标系，设PA＝m，BQ＝x，则P(0,0，m)，Q(1，x,0)，D(0，a,0)，

于是＝(1，x，－m)，＝(－1，a－x,0)

∵PQ⊥QD，∴·＝0即－1+ax－x²＝0

∴x²－ax+1＝0

∵只有一个点Q满足PQ⊥QD

∴方程x²－ax+1＝0只有一个实根，即

Δ＝a²－4＝0，∴a＝2(a>0)．

[答案]　2

8．空间四边形OABC中，OB＝OC，∠AOB＝∠AOC＝，则cos〈，〉的值是________．

[解析]　由条件得，cos〈，〉＝

＝

＝＝0.

[答案]　0

7．已知空间三点A、B、C坐标分别为(0,0,2)，(2,2,0)，(－2，－4，－2)，点P在xOy平面上且PA⊥AB，PA⊥AC，则P点坐标为________．

[解析]　设p＝(x，y，z)则＝(－x，－y,2－z)，＝(2,2，－2)，＝(－2，－4，－4)由已知得：

解得：∴p＝(－8,6,0)

[答案]　(－8,6,0)

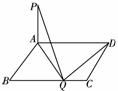
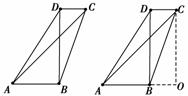
6．(2007·重庆卷)如图，在四边形ABCD中，||+||+||＝4，||·||+||·||＝4，||·||＝||·||＝0，则(||+||)·||的值为

(　)

A．2 　　　　　　　　　　　　　 　B．2

C．4　 　　　　　　　　　　　　 　D．4

[解析]　根据·＝·＝0可知，∠ABD＝∠BDC＝90°，则AB∥DC.

又由||+||+||＝4和||·||+||·||＝4，可解得BD＝2，AB+DC＝2.如图，延长AB，过C作CO⊥AB交AB延长线于点O.则有AO＝BD＝OC＝2，△AOC为等腰直角三角形．于是∠CAO＝45°，AC＝2.所以(+)·＝2×2×cos45°＝4.

[答案]　C

5．设点C(2a+1，a+1,2)在点P(2,0,0)、A(1，－3,2)、B(8，－1,4)确定的平面上，则a等于

(　)

A．16　 　　　　　　　　　　　　　　　　　　　　　 B．4

C．2　 　　　　　　　　　　　　　　　　　　　　　　 D．8

[解析]　＝(－1，－3,2)，＝(6，－1,4)．

根据共面向量定理，设＝x+y (x、y∈R)，则

(2a－1，a+1,2)＝x(－1，－3,2)+y(6，－1,4)

＝(－x+6y，－3x－y,2x+4y)，

∴

解得x＝－7，y＝4，a＝16.

[答案]　A