
16.(1)因为E,F分别是BC,CD的中点,
所以EF∥BD,……………………………2分
|
 平面PBD,BD
平面PBD,BD 平面PBD,
平面PBD,
所以EF∥平面PBD.………………………6分
(2)设BD交AC于点O,连结PO,
因为ABCD是菱形,所以BD⊥AC,O是BD中点,
又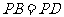 ,所以BD⊥PO,
,所以BD⊥PO,
又EF∥BD,所以EF⊥AC,EF⊥PO. ………………………10分
又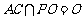 ,
,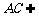 平面PAC,
平面PAC,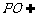 平面PAC,
平面PAC,
所以EF⊥平面PAC.……………………………………………………………………12分
因为EF 平面PEF,所以平面PEF⊥平面PAC.………………………………………14分
平面PEF,所以平面PEF⊥平面PAC.………………………………………14分
15.(1)在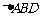 中,由正弦定理得
中,由正弦定理得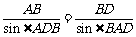 ①,
①,
在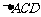 中,由正弦定理得
中,由正弦定理得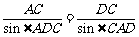 ②, ………………………2分
②, ………………………2分
又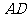 平分
平分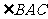 ,
,
所以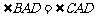 ,
,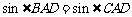 ,
,
 ,
,
由①②得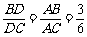 ,所以
,所以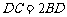 .………………………………………………6分
.………………………………………………6分
(2)因为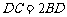 ,所以
,所以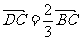 .
.
在△ 中,因为
中,因为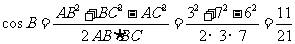 ,
…………10分
,
…………10分
所以
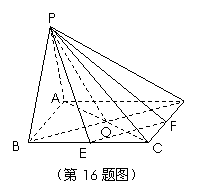
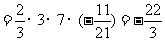 .………………………………………………………14分
.………………………………………………………14分
10. 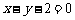 , 11.
, 11. 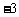 , 12. ②, 13.
, 12. ②, 13.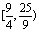 , 14. 2012.
, 14. 2012.
1. 2, 2.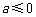 , 3.
, 3.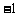 , 4.
, 4. 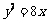 , 5.
, 5. 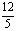 , 6. 36, 7.
, 6. 36, 7.  , 8.
, 8.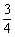 , 9.
, 9.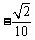 ,
,
23.(本小题满分10分)
设二项展开式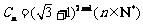 的整数部分为
的整数部分为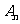 ,小数部分为
,小数部分为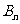 .
.
(1)计算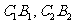 的值;
的值;
(2)求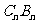 .
.
宿迁市2011届高三第一次调研试卷
数学1答案
一填空题:
22.(本小题满分10分)
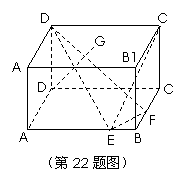
如图,在长方体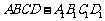 中,已知
中,已知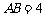 ,
,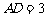 ,
,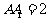 ,E,F分别是棱AB,BC 上的点,且
,E,F分别是棱AB,BC 上的点,且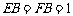 .
.
(1)求异面直线 与
与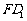 所成角的余弦值;
所成角的余弦值;
(2)试在面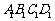 上确定一点G,使
上确定一点G,使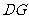
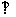 平面
平面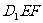 .
.
21.[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
(本小题满分10分)
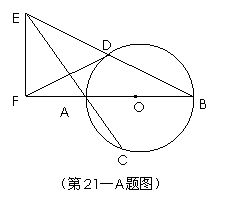 如图,
如图,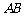 是⊙O的直径,弦
是⊙O的直径,弦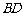 、
、 的延长线相交于点E,EF垂直BA的延长线于点F.求证:
的延长线相交于点E,EF垂直BA的延长线于点F.求证:
(1)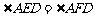 ;
;
(2)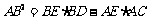 .
.
B.选修4-2:矩阵与变换
(本小题满分10分)
求曲线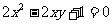 在矩阵MN对应的变换作用下得到的曲线方程,其中
在矩阵MN对应的变换作用下得到的曲线方程,其中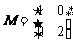 ,
,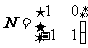 .
.
C.选修4-4:坐标系与参数方程
(本小题满分10分)
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度.已知直线l的极坐标方程为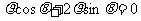 ,曲线C的参数方程为
,曲线C的参数方程为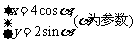 ,又直线l与曲线C交于A,B两点,求线段AB的长.
,又直线l与曲线C交于A,B两点,求线段AB的长.
D.选修4-5:不等式选讲
(本小题满分10分)
若存在实数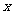 使
使 成立,求常数
成立,求常数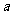 的取值范围.
的取值范围.
[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
20.(本小题满分16分)
已知函数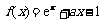 (
(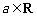 ,且a为常数).
,且a为常数).
(1)求函数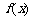 的单调区间;
的单调区间;
(2)当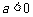 时,若方程
时,若方程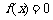 只有一解,求a的值;
只有一解,求a的值;
(3)若对所有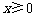 都有
都有 ,求a的取值范围.
,求a的取值范围.
数学Ⅱ(附加题)
19.(本小题满分16分)
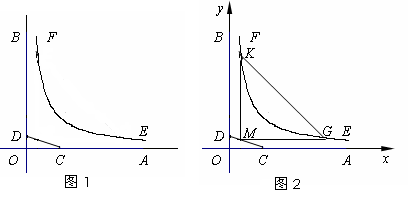
如图1,OA,OB是某地一个湖泊的两条垂直的湖堤,线段CD和曲线EF分别是湖泊中的一条栈桥和防波堤.为观光旅游需要,拟过栈桥CD上某点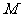 分别修建与OA,OB平行的栈桥MG,MK,且以MG,MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得CD的方程是
分别修建与OA,OB平行的栈桥MG,MK,且以MG,MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得CD的方程是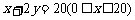 ,曲线EF的方程是
,曲线EF的方程是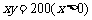 ,设点
,设点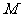 的坐标为
的坐标为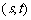 .(题中所涉及长度单位均为米,栈桥及防波堤都不计宽度)
.(题中所涉及长度单位均为米,栈桥及防波堤都不计宽度)
(1)求三角形观光平台MGK面积的最小值;
(2)若要使 的面积不小于320平方米,求
的面积不小于320平方米,求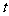 的范围.
的范围.
18.(本小题满分16分)
已知椭圆E: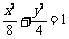 的左焦点为F,左准线
的左焦点为F,左准线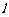 与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
(1)求圆C的方程;
(2)若直线FG与直线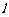 交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在一点P,使得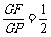 ?若存在,求出点P坐标;若不存在,请说明理由.
?若存在,求出点P坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com