3．处理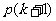 时不善于“拆、分、并、补”等配凑技巧的应用(原因：缺乏目标意识)。4。不能灵活运用其它证明不等式的方法，如比较法、分析法、综合法、放缩法(原因：对 “数学归纳法”缺乏认识，忽略了应用数学归纳法证题时可以结合其它数学方法)。

应用数学归纳法解题要注意：递推基础不可少，归纳假设要用到，结论写明莫忘掉。

2．若命题中n为正奇数(或正偶数)，在第二步假设“n=k时命题成立”，误认为需证明“n=k+1时命题也成立”( 错因：忽略相邻的正奇数相差2)。

教学中学生可能遇到的障碍有：

1.由“n=k”到“n=k+1”时项的确定(产生此障碍的原因：没弄清计数规律，这类问题，通常按“找规律，定项数”的方法来处理)。

3．在研究数列的探索性问题时，数学归纳法常与不完全归纳法结合使用，其一般解题步骤是：归纳一猜想一证明。

2．用数学归纳法证题时，难在第二步，要顺利完成这一步主要依赖于观察、归纳、恒等变形等方面的能力，在推导证明中，必须用到“归纳假设”，否则就不是数学归纳法。

1．数学归纳法中第1步是递推的基础(其中的n₀不一定为1)，第2步是递推的依据，“假设n=k(k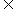N^※，k≥n₀)时命题成立”叫做归纳假设。

4.培养学生数学思维的严谨性。

目标解析：

3.培养学生综合运用知识的能力及解题时的目标意识。

2．掌握为证n＝k+1成立的常见变形技巧：提公因式、添项、拆项、合并项、配方等.

目标：理解数学归纳法的原理，能用数学归纳法证明一些简单的数学命题。

1．理解数学归纳法，进一步掌握其实质与步骤．