
6.过点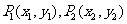 的直线
的直线 交直线
交直线 于点
于点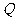 ,则点
,则点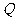 分有向线段
分有向线段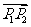 的比为________
的比为________
5.点 M(-1, 0)关于直线x+2y-1=0对称点 的坐标是
;
的坐标是
;
4.如果直线l:x+ay+2=0平行于直线2x-y+3=0,则直线l在两坐标轴上截距之和是
 ( )
( )
A.6 B.2 C.-1 D.-2
3.已知直线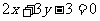 和
和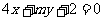 互相平行,则两直线之间的距离是( )
互相平行,则两直线之间的距离是( )
A. B. C. 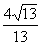
 D.
D. 4
4
2.过点A(1,2)且与原点距离最大的直线方程是( )
A. 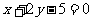 B.
B.  C
C 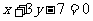 D.
D. 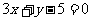 [来源:Z_X_X_K]
[来源:Z_X_X_K]
1.若直线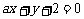 与连接两点
与连接两点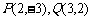 的线段相交,则实数a的取值范围( )
的线段相交,则实数a的取值范围( )
A.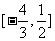 B.
B.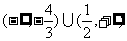
C.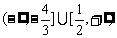 D.
D.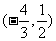
10、(1)若不等式 的解集是空集,求实数a 的取值范围。
(2)对于一切实数x ,若 恒成立,求实数m 的取值范围。
(3)不等式 对一切实数x都成立,求实数m的取值范围
类型十二:解分式不等式
求不等式 的解集
类型十三:含参数的不等式
解关于X的不等式
类型一:简单命题的概念
例1 判断下列语句是否是命题,若不是,说明理由;若是,判断命题的真假.
(1) 奇数的平方仍然是奇数;
(2) 两对角线垂直的四边形是菱形;
(3) 所有的质数都是奇数;
(4) 5x>4x;
(5) x2+x+1>0;
(6) “等边三边形难道不是等腰三角形吗?”
(7) 未来是多么美好啊!
(8) 把数学课本给我带来;
(9) x+y是有理数,则x,y都是有理数.
类型二:复合命题的构成问题
例2 分别指出下列复合命题的形式及构成它的简单命题:
(1) x=2或x=3是方程x2-5x+6=0的根;
(2) 既大于3又是无理数;
(3) 直角不等于90o
(4) x+1 x-3;
(5) 垂直于弦的直径平分这条弦,并且平分该弦所对的两条弧.
类型三:复合命题真假的判断问题
例3 判断由下列各组命题构成的“p或q”,“p且q”,“非p”形式的复合命题的真假.
(1) p:3>3; q:3=3;
(2)
(3) p:函数y=x2+3x-4的图像与x轴没有公共点; q:方程x2+3x-4=0没有实根.
类型四:命题的否定问题
例4 写出下列命题的否定形式:
(1) a>0或b≤0;
(2) 矩形的四个角都是直角;
(3) 全等三角形一定是相似三角形;
(4) 4>3;
(5) 至多有两个解.
类型五:复合命题的综合运用问题
例5 已知命题p:方程x2+mx+1=0有两个不等的负实数根,命题q:方程4x2+4(m-2)x+1=0无实数根,若“p或q”为真命题,“p且q”为假命题,求m的取值范围.
类型六:四种命题的概念问题
例6 把下列命题写成“若p则q”的形式,并写出它们的逆命题、否命题和逆否命题.
(1) ;
(2) 对顶角相等;
(3) 已知a,b,c,d是实数,当a=b,c=d时,a+c=b+d;
类型七:四种命题真假判断问题
例7 若 写出逆命题、否命题、逆否命题,同时分别指出它们的真假
类型八:用反正法证明
例8 设 .求证:a,b,c中至少有一个数大于0.
类型九:充分条件、必要条件的概念与判断
例9 判断下列各题中p是q的条件:
(1) ;
(2) p:四边形四边相等;q:四边形为正方形;
(3)
(4)
类型十:充要条件的证明问题
例10 .
类型十一:求充要条件的问题
例11 已知关于 的方程 , ,求方程有两个正根的充要条件.
9、解不等式(1)
类型十: 型不等式的解法
(2) (3)
类型十:含多个绝对值不等式的解法
(4)
类型十一:恒成立问题
8、设 ,
若A∩B=B,求a的值;
若A∪B=B,求a的值;
类型九: 型不等式的解法
7、
类型八:有关交集、并集、补集的综合运用问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com