
19.(1)由题意,得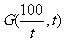 ,
,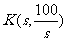
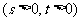 ,
,
又因为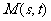 在线段CD:
在线段CD: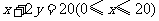 上,
上,
所以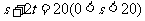 ,
,
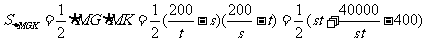 ……………4分
……………4分
由 ,得
,得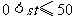 ,当且仅当
,当且仅当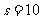 ,
,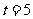 时等号成立.
时等号成立.
……………………………………6分
令 ,则
,则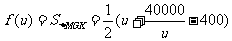 ,
,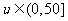 .
.
又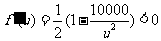 ,故
,故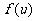 在
在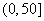 上单调递减,
上单调递减,
(注意:若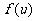 在
在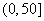 上单调递减未证明扣1分)
上单调递减未证明扣1分)
所以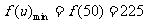 ,此时
,此时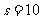 ,
,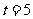 .
.
所以三角形MGK面积的最小值为225平方米. ……………………………………10分
(2)由题意得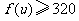 ,
,
当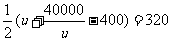 ,解得
,解得 或
或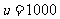 (舍去),
(舍去),
由(1)知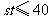 ,
……………………………………14分
,
……………………………………14分
即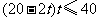 ,解之得
,解之得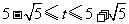 .
.
所以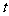 的范围是
的范围是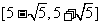 .………………………………………………………16分
.………………………………………………………16分
18.(1)由椭圆E: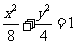 ,得
,得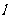 :
: ,
,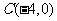 ,
,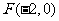 ,
,
又圆C过原点,所以圆C的方程为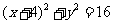 .………………………………4分
.………………………………4分
(2)由题意,得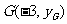 ,代入
,代入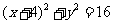 ,得
,得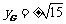 ,
,
所以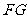 的斜率为
的斜率为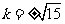 ,
,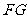 的方程为
的方程为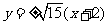 , …………………8分
, …………………8分
(注意:若点G或FG方程只写一种情况扣1分)
所以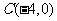 到
到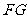 的距离为
的距离为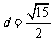 ,直线
,直线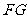 被圆C截得弦长为
被圆C截得弦长为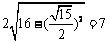 .
.
故直线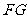 被圆C截得弦长为7.…………………………………………………………10分
被圆C截得弦长为7.…………………………………………………………10分
(3)设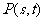 ,
,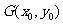 ,则由
,则由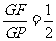 ,得
,得 ,
,
整理得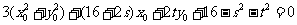 ①,…………………………12分
①,…………………………12分
又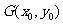 在圆C:
在圆C: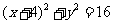 上,所以
上,所以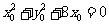 ②,
②,
②代入①得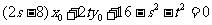 , …………………………14分
, …………………………14分
又由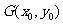 为圆C 上任意一点可知,
为圆C 上任意一点可知,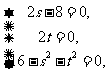 解得
解得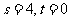 .
.
所以在平面上存在一点P,其坐标为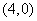 .
…………………………16分
.
…………………………16分
17.(1)设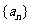 公比为q,由题意得
公比为q,由题意得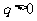 ,
,
且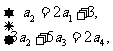 即
即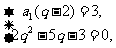 ……………………………………………2分
……………………………………………2分
解之得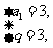 或
或 (舍去),…………………………………………………4分
(舍去),…………………………………………………4分
所以数列 的通项公式为
的通项公式为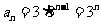 ,
,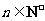 .…………………………………6分
.…………………………………6分
(2)由(1)可得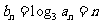 ,所以
,所以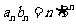 .…………………………………8分
.…………………………………8分
所以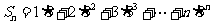 ,
,
所以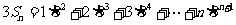 ,
,
两式相减得,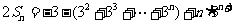 …………………………………10分
…………………………………10分

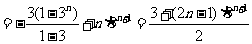 ,
,
所以数列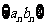 的前n项和为
的前n项和为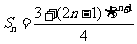 . ………………………………14分
. ………………………………14分
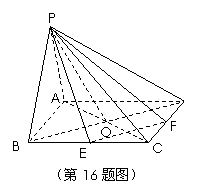
16.(1)因为E,F分别是BC,CD的中点,
所以EF∥BD,……………………………2分
|
 平面PBD,BD
平面PBD,BD 平面PBD,
平面PBD,
所以EF∥平面PBD.………………………6分
(2)设BD交AC于点O,连结PO,
因为ABCD是菱形,所以BD⊥AC,O是BD中点,
又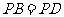 ,所以BD⊥PO,
,所以BD⊥PO,
又EF∥BD,所以EF⊥AC,EF⊥PO. ………………………10分
又 ,
,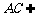 平面PAC,
平面PAC,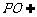 平面PAC,
平面PAC,
所以EF⊥平面PAC.……………………………………………………………………12分
因为EF 平面PEF,所以平面PEF⊥平面PAC.………………………………………14分
平面PEF,所以平面PEF⊥平面PAC.………………………………………14分
15.(1)在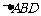 中,由正弦定理得
中,由正弦定理得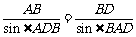 ①,
①,
在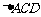 中,由正弦定理得
中,由正弦定理得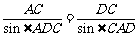 ②, ………………………2分
②, ………………………2分
又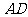 平分
平分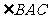 ,
,
所以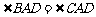 ,
,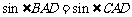 ,
,
 ,
,
由①②得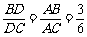 ,所以
,所以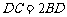 .………………………………………………6分
.………………………………………………6分
(2)因为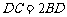 ,所以
,所以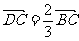 .
.
在△ 中,因为
中,因为 ,
…………10分
,
…………10分
所以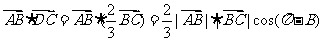
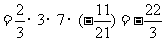 .………………………………………………………14分
.………………………………………………………14分
10. 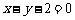 , 11.
, 11. 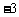 , 12. ②, 13.
, 12. ②, 13. , 14. 2012.
, 14. 2012.
1. 2, 2.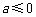 , 3.
, 3. , 4.
, 4. 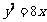 , 5.
, 5. 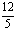 , 6. 36, 7.
, 6. 36, 7.  , 8.
, 8.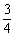 , 9.
, 9.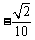 ,
,
23.(本小题满分10分)
设二项展开式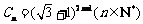 的整数部分为
的整数部分为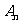 ,小数部分为
,小数部分为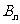 .
.
(1)计算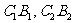 的值;
的值;
(2)求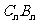 .
.
宿迁市2011届高三第一次调研试卷
数学1答案
一填空题:
22.(本小题满分10分)
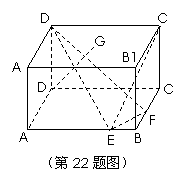
如图,在长方体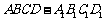 中,已知
中,已知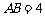 ,
,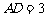 ,
,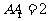 ,E,F分别是棱AB,BC 上的点,且
,E,F分别是棱AB,BC 上的点,且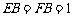 .
.
(1)求异面直线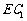 与
与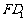 所成角的余弦值;
所成角的余弦值;
(2)试在面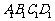 上确定一点G,使
上确定一点G,使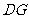
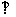 平面
平面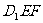 .
.
21.[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
(本小题满分10分)
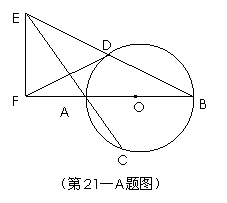 如图,
如图,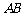 是⊙O的直径,弦
是⊙O的直径,弦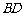 、
、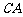 的延长线相交于点E,EF垂直BA的延长线于点F.求证:
的延长线相交于点E,EF垂直BA的延长线于点F.求证:
(1)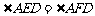 ;
;
(2)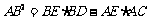 .
.
B.选修4-2:矩阵与变换
(本小题满分10分)
求曲线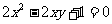 在矩阵MN对应的变换作用下得到的曲线方程,其中
在矩阵MN对应的变换作用下得到的曲线方程,其中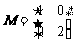 ,
,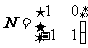 .
.
C.选修4-4:坐标系与参数方程
(本小题满分10分)
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度.已知直线l的极坐标方程为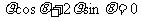 ,曲线C的参数方程为
,曲线C的参数方程为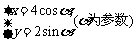 ,又直线l与曲线C交于A,B两点,求线段AB的长.
,又直线l与曲线C交于A,B两点,求线段AB的长.
D.选修4-5:不等式选讲
(本小题满分10分)
若存在实数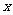 使
使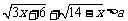 成立,求常数
成立,求常数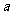 的取值范围.
的取值范围.
[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com