
3.下列化学反应的离子方程式正确的是
A.用饱和碳酸钠溶液吸收过量的二氧化碳: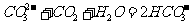
B.向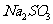 、NaI的混合溶液中滴加少量氯水:
、NaI的混合溶液中滴加少量氯水: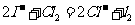
C.将NaOH溶液滴入过量的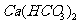 溶液中:
溶液中:
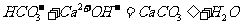
D.硫化钠的水解反应:
2.下图为课本中的插图,下列操作不合理的是

A.切割钠 B.过氧化钠与水反应
C.钾的焰色反应 D.铜在氯气中燃烧
1.南阳将于2012年承办第七届全国农动会。下列措施有利于节能减排、改善环境质量的有
①南阳将大力发展抽水蓄能电、核电、风力发电,以减少火力发电带来的二氧化硫和二氧化碳排放问题
②积极推行“限塑令”,加快研发利用二氧化碳合成的聚碳酸酯类可降解塑料
③推广使用乙醇汽油,以减少汽车尾气排放问题
④发展低碳经济、循环经济.推广可利用太阳能、风能的城市照明系统
⑤使用生物酶降解生活废水中的有机物,使用填埋法处理未经分类的生活垃圾
A.①②③④ B.①②⑤ C.①②④⑤ D.③④⑤
2. 已知中心在原点的双曲线C的右焦点为(2,0),右顶点为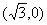 。
。
(1) 求双曲线C的方程;
(2)
若直线l: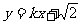 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且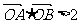 (其中O为原点),求k的取值范围。
(其中O为原点),求k的取值范围。
教学反思:
由于向量既能体现“形”的直观位置特征,又具有“数”的良好运算性质,是数形结合与转换的桥梁和纽带。而解析几何也具有数形结合与转换的特征,所以在向量与解析几何知识的交汇处设计试题,已逐渐成为高考命题的一个新的亮点。本节问题立足基础,适当综合,巧设问题,分类解析,有条理有内容有方法有深度,正确理解和发动学生多看、多想、多操作、多反思总结,突出学生主体地位,较好的完成教学目标。
附板书设计:
|
3.⑴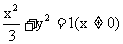 ⑵ k的取值范围是(-1,1)。
⑵ k的取值范围是(-1,1)。
从上述几例可以看出,只要对于解析几何中图形的位置关系和数量关系进行认真分析,充分挖掘问题的向量背景,注意运用曲线参数方程的点化作用,就完全有可能获得一个漂亮的向量解法。
课时小结
向量具有数形兼备的特点,成为了作为联系众多知识的桥梁,向量与三角、解析几何、立体几何的交汇是当今高考命题的必然趋势,本节处理了三类问题,即利用向量解决解析几何中有关平行、共线问题,长度、角度、垂直及轨迹和综合应用问题。
布置作业:
1已知椭圆方程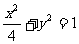 ,过B(-1,0)的直线l交随圆于C、D两点,交直线x=-4于E点,B、E分
,过B(-1,0)的直线l交随圆于C、D两点,交直线x=-4于E点,B、E分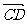 的比分λ1、λ2.
的比分λ1、λ2.
求证:λ1+λ2=0
3.已知点G是△ABC的重心,A(0, -1),B(0, 1),在x轴上有一点M,满足|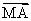 |=|
|=|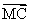 |,
|,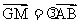 (
(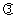 ∈R).
∈R).
⑴求点C的轨迹方程;
⑵若斜率为k的直线l与点C的轨迹交于不同两点P,Q,且满足|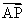 |=|
|=|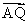 |,试求k的取值范围.
|,试求k的取值范围.
答案1.B 2.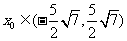
2、已知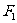 ,
, 椭圆
椭圆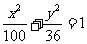 的两个焦点,P(
的两个焦点,P(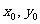 )为椭圆上一点,
)为椭圆上一点,
当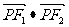 <0时,
<0时,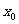 的取值范围为_________.。
的取值范围为_________.。
1、平面直角坐标系中,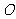 为坐标原点,已知
为坐标原点,已知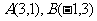 ,若点
,若点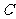 满足
满足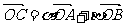 ,其中
,其中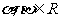 ,且
,且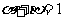 ,则点
,则点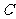 的轨迹方程为( )
的轨迹方程为( )
A. 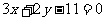 B.
B. 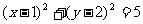
C. 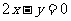 D.
D. 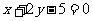
3、运用平面向量综合知识,探求动点轨迹方程,还可再进一步探求曲线的性质。
例2.已知 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设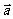 =
=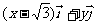 ,
, 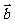 =
=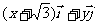 ,且满足|
,且满足|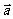 |+|
|+|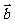 |=4.
|=4.
⑴求点P(x,y)的轨迹C的方程.
⑵如果过点Q(0,m)且方向向量为 =(1,1) 的直线l与点P的轨迹交于A,B两点,当
=(1,1) 的直线l与点P的轨迹交于A,B两点,当 AOB的面积取到最大值时,求m的值。
AOB的面积取到最大值时,求m的值。
解:(1)
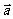 =
=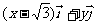 , |
, |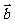 |=
|=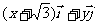 ,且|
,且|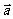 |+|
|+|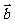 |=4.
|=4.
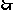 点P(x,y)到点(
点P(x,y)到点(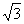 ,0),(-
,0),(-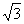 ,0)的距离这和为4,故点P的轨迹方程为
,0)的距离这和为4,故点P的轨迹方程为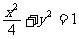
(2)设A(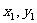 ),B(
),B(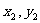 )依题意直线AB的方程为y=x+m.代入椭圆方程,得
)依题意直线AB的方程为y=x+m.代入椭圆方程,得 ,则
,则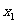 +
+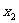 =-
=- m,
m,
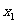

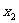 =
=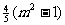
因此,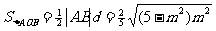
当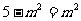 时,即m=
时,即m=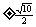 时,
时,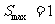
[变式1] 已知 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设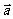 =
=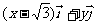 ,
, 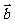 =
=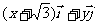 ,且满足||
,且满足||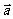 |-|
|-|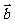 ||=2.求点P(x,y)的轨迹C的方程.(轨迹为双曲线)
||=2.求点P(x,y)的轨迹C的方程.(轨迹为双曲线)
[变式2] 已知 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设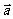 =
=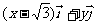 ,
, 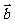 =
=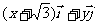 ,且满足
,且满足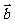

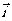 =|
=|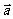 |.求点P(x,y)的轨迹C的方程.
|.求点P(x,y)的轨迹C的方程.
[提示:设K(-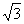 ,0),F (
,0),F (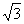 ,0),则
,0),则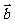

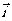 表示
表示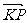 在x轴上射影,即点P到x= -
在x轴上射影,即点P到x= -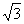 的距离,所以点P到定点F的距离与到定直线x= -
的距离,所以点P到定点F的距离与到定直线x= -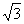 的距离比为1,故点P的轨迹是以(
的距离比为1,故点P的轨迹是以(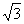 ,0)为焦点以x= -
,0)为焦点以x= -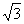 为准线抛物线]
为准线抛物线]
巩固训练
2.运用向量的数量积处理解几中有关长度、角度、垂直等问题
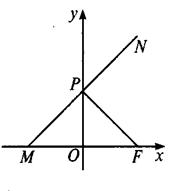 例2如图,点F(a,0)(a>0),点P 在y轴上运动,点M在x轴上运动,点N为动点,且
例2如图,点F(a,0)(a>0),点P 在y轴上运动,点M在x轴上运动,点N为动点,且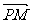 ·
·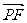 =0,
=0,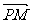 +
+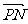 =0。
=0。
(1)求点N的轨迹C的方程;
(2)过点F(a ,0)的直线l(不与x轴垂直)与曲线C交于A、B两点,设点K(-a,0),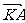 与
与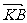 的夹角为θ,
的夹角为θ,
求证:0<θ<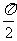 .
.
[分析] (1)分别设出P、M与N点的坐标,将已知向量坐标化,然后利用向量数量积及向量相等知识找到等量关系。
(2)利用向量的夹角公式可知,要证0<θ<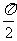 ,只要证
,只要证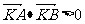 。
。
[解析] (1)y2=4ax
(2) 证明:设AB的方程为y=k(x-a),代入y2=4ax得
k2x2-2a(k2+2)x+k2a2=0
设A(x1 , y1)、B(x2 , y2),则
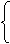 x1+x2=
x1+x2=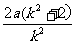
x1 x2=a2
∵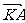 =(x1+a , y1),
=(x1+a , y1), 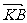 =(x2+a , y2)
=(x2+a , y2)
∴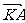 ·
·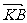 =(x1+a)(x2+a)+y1 y2
=(x1+a)(x2+a)+y1 y2
=x1x2+a ( x1+x2)+a2+(-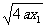 ) · (
) · (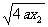 )
)
=a2+a·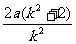 + a2-4a2=
+ a2-4a2=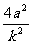 >0,
>0,
∵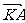 与
与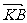 的夹角为θ,
的夹角为θ,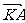 与
与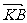 不共线,
不共线,
∴θ≠0,∴cosθ=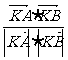 >0 , 即0<θ<
>0 , 即0<θ<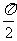 .
.
变式:给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点。
(Ⅰ)设l的斜率为1,求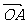 与
与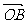 夹角的大小;
夹角的大小;
[解答] (Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为
y=x-1,将y=x-1代入方程y2=4x,并整理得x2-6x+1=0
设A(x1,y1),B(x2,y2),则有x1+x2=6, x1x2=1,
从而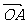 ·
·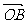 =x1x2+y1y2=2x1x2-(x1+x2)+1=-3
=x1x2+y1y2=2x1x2-(x1+x2)+1=-3
︱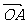 ︱·︱
︱·︱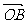 ︱=
︱=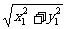 ·
·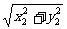 =
=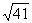 ,
,
cos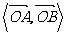 =
=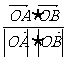 =
=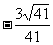
所以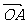 与
与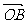 夹角的大小为π-arcos
夹角的大小为π-arcos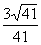 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com