
1、函数的概念:
(1)映射:设非空数集A,B,若对集合A中任一元素a,在集合B中有唯一元素b与之对应,则称从A到B的对应为映射,记为f:A→B,f表示对应法则,b=f(a)。
(2)函数定义:函数就是定义在非空数集A,B上的映射,此时称数集A为定义域,象集C={f(x)|x∈A}为值域。定义域,对应法则,值域构成了函数的三要素,从逻辑上讲,定义域,对应法则决定了值域,是两个最基本的因素。逆过来,值域也会限制定义域。
在中学数学的各个部分都存在着求取值范围这一典型问题,它的一种典型处理方法就是建立函数解析式,借助于求函数值域的方法。
2、函数图像、性质的运用。
3导数的定义及其应用
1、函数的定义及通性;
22.已知数列
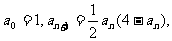
(1)证明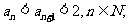
(2)求数列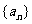 的通项公式an.
的通项公式an.
21. 已知函数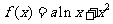 (
(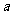 为实常数).
为实常数).
(Ⅰ) 若 ,求证:函数
,求证:函数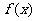 在
在 上是增函数;
上是增函数;
(Ⅱ) 若存在x∈[1,e],使得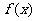 ≤
≤ 成立,求实数
成立,求实数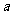 的取值范围;
的取值范围;
(Ⅲ) 求函数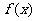 在[1,e]上的最小值及相应的x值。
在[1,e]上的最小值及相应的x值。
20.设二次函数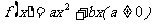 满足条件:①
满足条件:① ;②函数
;②函数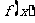 的图象与直线
的图象与直线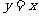 相切.
相切.
(I)求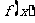 的解析式;
的解析式;
(II)若不等式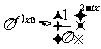 在
在 时恒成立,求实数
时恒成立,求实数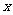 的取值范围.
的取值范围.
19.已知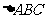 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为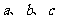 ,向量
,向量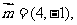
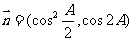 ,且
,且 .
.
(1)求角A的大小;
(2)若 ,试判断
,试判断 取得最大值时
取得最大值时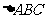 形状.
形状.
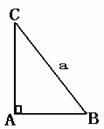
18.如图,在Rt△ABC中,已知BC=a.若长为2a的线段PQ以点A为中点,问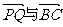 的夹 角θ取何值时
的夹 角θ取何值时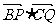 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
17.设命题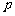 :关于
:关于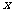 的不等式
的不等式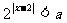 的解集为
的解集为 ;命题
;命题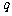 :函数
:函数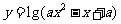 的值域是
的值域是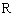 .如果命题
.如果命题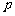 和
和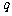 有且仅有一个正确,求实数
有且仅有一个正确,求实数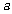 的取值范围.
的取值范围.
16.给定正整数 按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,
按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,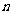 ,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依次类推,最后一行(第
,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依次类推,最后一行(第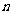 行)只有一个数,例如
行)只有一个数,例如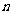 =6时数表如图所,则当
=6时数表如图所,则当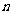 =2009时最后一行的数是___ .
=2009时最后一行的数是___ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com