
1.在横线处仿写前面的句子,构成一组排比句。
每一汪水塘里,都有海洋的气息;______ ______,____ _______;
___ _______,_______ ___。所以诗人才说:“一株三叶草,再加上我的想象,便是一片广阔的草原。”
(三) 解答题
11、设定义在[-2,2]上的偶函数f(x)在区间[0,2]上单调递减,若f(1-m)<f(m),求实数m的取值范围。
12.(2009陕西卷文)(本小题满分12分)
已知函数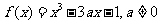
 求
求 的单调区间;
的单调区间;
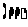 若
若 在
在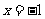 处取得极值,直线y=my与
处取得极值,直线y=my与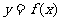 的图象有三个不同的交点,求m的取值范围。
的图象有三个不同的交点,求m的取值范围。
世纪教育网解析:(1)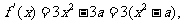
当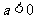 时,对
时,对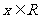 ,有
,有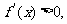
当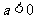 时,
时, 的单调增区间为
的单调增区间为
当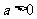 时,由
时,由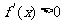 解得
解得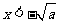 或
或 ;
;
由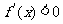 解得
解得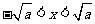 ,
,
当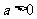 时,
时, 的单调增区间为
的单调增区间为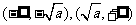 ;
; 的单调减区间为
的单调减区间为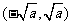 。
。
(2)因为 在
在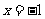 处取得极大值,
处取得极大值,
所以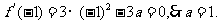
所以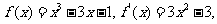
由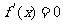 解得
解得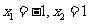 。
。
由(1)中 的单调性可知,
的单调性可知, 在
在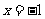 处取得极大值
处取得极大值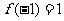 ,
,
在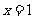 处取得极小值
处取得极小值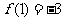 。
。
因为直线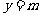 与函数
与函数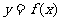 的图象有三个不同的交点,又
的图象有三个不同的交点,又 ,
,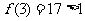 ,
,
结合 的单调性可知,
的单调性可知,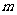 的取值范围是
的取值范围是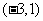 。
。
附:福建高考自主命题2004-2009年文科解答题展示
(2004文22).(本小题满分14分)
已知f(x)=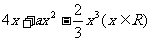 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=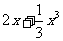 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
22.本题主要考查函数的单调性,导数的应用和不等式等有关知识,考查数形结合及分类讨论思想和灵活运用数学知识分析问题和解决问题的能力.满分14分.
解:(Ⅰ)f'(x)=4+2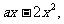 ∵f(x)在[-1,1]上是增函数,
∵f(x)在[-1,1]上是增函数,
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设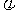 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:
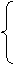
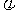 (1)=1-a-2≤0,
(1)=1-a-2≤0,
① 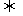
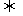 -1≤a≤1,
-1≤a≤1,
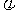 (-1)=1+a-2≤0.
(-1)=1+a-2≤0.
∵对x∈[-1,1],只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
方法二:
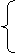
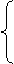
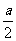 ≥0,
≥0,
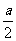 <0,
<0,
①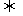 或
或
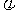 (-1)=1+a-2≤0
(-1)=1+a-2≤0 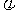 (1)=1-a-2≤0
(1)=1-a-2≤0
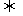 0≤a≤1
或 -1≤a≤0
0≤a≤1
或 -1≤a≤0
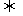 -1≤a≤1.
-1≤a≤1.
∵对x∈[-1,1],只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
(Ⅱ)由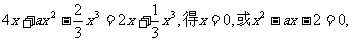
∵△=a2+8>0
∴x1,x2是方程x2-ax-2=0的两非零实根,
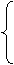 x1+x2=a,
x1+x2=a,
∴
从而|x1-x2|=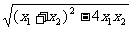 =
=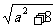 .
.
x1x2=-2,
∵-1≤a≤1,∴|x1-x2|= ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
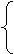 g(-1)=m2-m-2≥0,
g(-1)=m2-m-2≥0,
② 
g(1)=m2+m-2≥0,
 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二:
当m=0时,②显然不成立;
当m≠0时,

 m>0,
m<0,
m>0,
m<0,
②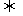 或
或
g(-1)=m2-m-2≥0 g(1)=m2+m-2≥0
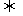 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
(2005文20).(本小题满分12分)
已知函数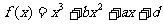 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为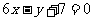 .
.
(Ⅰ)求函数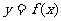 的解析式;
的解析式;
(Ⅱ)求函数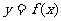 的单调区间.
的单调区间.
解:(I)由函数的图像经过点(0,2)可知,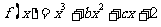 ,
,
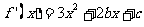 ,∵
,∵ 在点M(-1,f(-1))处的切线方程为
在点M(-1,f(-1))处的切线方程为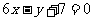 .
.
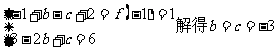 ,
,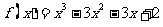
(II)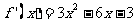
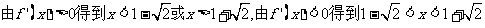

(2006文21) (本小题满分12分)
已知 是二次函数,不等式
是二次函数,不等式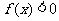 的解集是
的解集是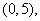 且
且 在区间
在区间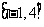 上的最大值是12。
上的最大值是12。
(I)
求 的解析式;
的解析式;
(II)
是否存在实数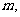 使得方程
使得方程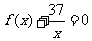 在区间
在区间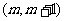 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出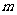 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(21) 本小题主要考查函数的单调性、极值等基本知识,考查运用导数研究函数的性质的方法,考查函数与方程、数形结合等数学思想方法和分析问题、解决问题的能力。满分12分。
(I)
解:
 是二次函数,且
是二次函数,且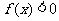 的解集是
的解集是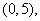
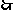 可设
可设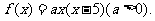
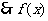 在区间
在区间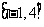 上的最大值是
上的最大值是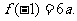
由已知,得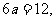
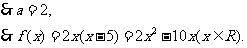
(II)
方程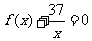 等价于方程
等价于方程
设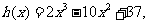
则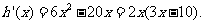
当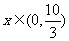 时,
时,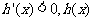 是减函数;
是减函数;
当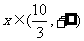 时,
时, 是增函数。
是增函数。
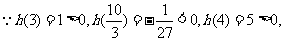
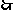 方程
方程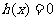 在区间
在区间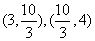 内分别有惟一实数根,而在区间
内分别有惟一实数根,而在区间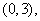
 内没有实数根,
内没有实数根,
所以存在惟一的自然数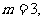 使得方程
使得方程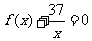 在区间
在区间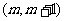 内有且只有两个不同的实数根。
内有且只有两个不同的实数根。
(2007文20) (本小题满分12分)
(本小题满分12分)
设函数

(Ⅰ)求 的最小值
的最小值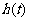 ;
;
(Ⅱ)若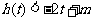 对
对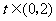 恒成立,求实数
恒成立,求实数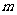 的取值范围
的取值范围
20 本题主要考查函数的单调性、极值以及函数导数的应用,考查运用数学知识分析问题解决问题的能力
本题主要考查函数的单调性、极值以及函数导数的应用,考查运用数学知识分析问题解决问题的能力 满分12分
满分12分
解:(Ⅰ)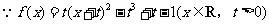 ,
,
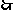 当
当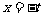 时,
时, 取最小值
取最小值 ,
,
即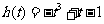

(Ⅱ)令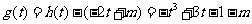 ,
,
由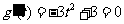 得
得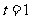 ,
,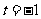 (不合题意,舍去)
(不合题意,舍去)
当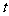 变化时
变化时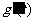 ,
,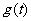 的变化情况如下表:
的变化情况如下表:
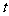 |
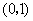 |
 |
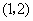 |
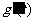 |
 |
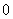 |
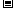 |
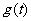 |
递增↗ |
极大值 |
递减↘ |
 在
在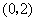 内有最大值
内有最大值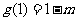

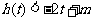 在
在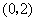 内恒成立等价于
内恒成立等价于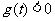 在
在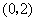 内恒成立,
内恒成立,
即等价于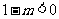 ,
,
所以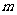 的取值范围为
的取值范围为

(2008文21)(本小题满分12分)
已知函数 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数 的图象关于y轴对称.
的图象关于y轴对称.
(Ⅰ)求m、n的值及函数y=f(x)的单调区间;
(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
(21)本小题主要考察函数的奇偶性、单调性、极值、导数、不等式等基础知识,考查运用导数研究函数性质的方法,以及分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.满分12分.
解:(1)由函数f(x)图象过点(-1,-6),得m-n=-3, ……①
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n;
而g(x)图象关于y轴对称,所以-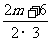 =0,所以m=-3,
=0,所以m=-3,
代入①得n=0.
于是f′(x)=3x2-6x=3x(x-2).
由f′(x)>得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);
由f′(x)<0得0<x<2,
故f(x)的单调递减区间是(0,2).
(Ⅱ)由(Ⅰ)得f′(x)=3x(x-2),
令f′(x)=0得x=0或x=2.
当x变化时,f′(x)、f(x)的变化情况如下表:
|
X |
(-∞.0) |
0 |
(0,2) |
2 |
(2,+ ∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
 |
极大值 |
|
极小值 |
|
由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值;
当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,f(x)有极小值-6,无极大值;当a=1或a≥3时,f(x)无极值.
(2009文21).(本小题满分12分)
已知函数 且
且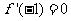
(I)试用含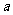 的代数式表示
的代数式表示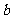 ;
;
(Ⅱ)求 的单调区间;
的单调区间; 

(Ⅲ)令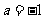 ,设函数
,设函数 在
在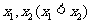 处取得极值,记点
处取得极值,记点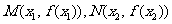 ,证明:线段
,证明:线段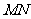 与曲线
与曲线 存在异于
存在异于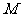 、
、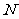 的公共点;
的公共点;
解法一:
(I)依题意,得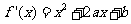
由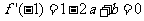 得
得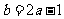
(Ⅱ)由(I)得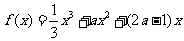 (
(
故
令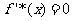 ,则
,则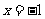 或
或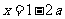
①当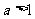 时,
时,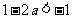
当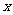 变化时,
变化时,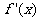 与
与 的变化情况如下表:
的变化情况如下表:
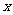 |
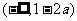 |
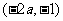 |
 |
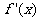 |
+ |
- |
+ |
 |
单调递增 |
单调递减 |
单调递增 |
由此得,函数 的单调增区间为
的单调增区间为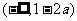 和
和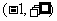 ,单调减区间为
,单调减区间为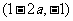
②由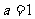 时,
时,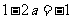 ,此时,
,此时,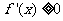 恒成立,且仅在
恒成立,且仅在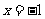 处
处 ,故函数
,故函数 的单调区间为R
的单调区间为R
③当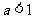 时,
时,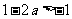 ,同理可得函数
,同理可得函数 的单调增区间为
的单调增区间为 和
和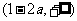 ,单调减区间为
,单调减区间为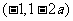
综上:
当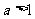 时,函数
时,函数 的单调增区间为
的单调增区间为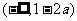 和
和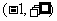 ,单调减区间为
,单调减区间为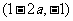 ;
;
当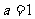 时,函数
时,函数 的单调增区间为R;
的单调增区间为R;
当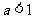 时,函数
时,函数 的单调增区间为
的单调增区间为 和
和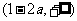 ,单调减区间为
,单调减区间为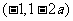
(Ⅲ)当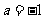 时,得
时,得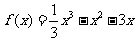
由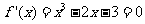 ,得
,得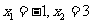
由(Ⅱ)得 的单调增区间为
的单调增区间为 和
和 ,单调减区间为
,单调减区间为
所以函数 在
在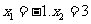 处取得极值。
处取得极值。
故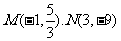
所以直线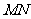 的方程为
的方程为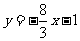
由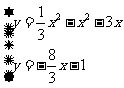 得
得

令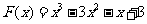
易得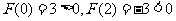 ,而
,而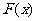 的图像在
的图像在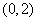 内是一条连续不断的曲线,
内是一条连续不断的曲线,
故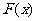 在
在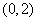 内存在零点
内存在零点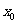 ,这表明线段
,这表明线段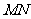 与曲线
与曲线 有异于
有异于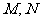 的公共点
的公共点
解法二:
(I)同解法一
(Ⅱ)同解法一。
(Ⅲ)当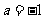 时,得
时,得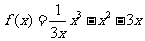 ,由
,由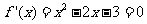 ,得
,得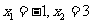
由(Ⅱ)得 的单调增区间为
的单调增区间为 和
和 ,单调减区间为
,单调减区间为 ,所以函数
,所以函数 在
在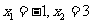 处取得极值,
处取得极值,
故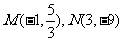
所以直线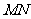 的方程为
的方程为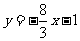

由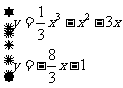 得
得
解得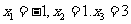

所以线段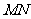 与曲线
与曲线 有异于
有异于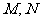 的公共点
的公共点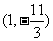

(二) 填空题
6、已知定义在R的奇函数f(x)满足f(x+2)=-f(x),且当0≤x≤1时,f(x)=x,则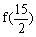 =__________。
=__________。
7、 已知y=loga(2-x)是x的增函数,则a的取值范围是__________。
8、 函数f(x)定义域为[1,3],则f(x2+1)的定义域是__________。
9、函数f(x)=x2-bx+c满足f(1+x)=f(1-x),且f(0)=3,则f(bx)与f(cx)的大小关系是__________。
10、已知A={y|y=x2-4x+6,y∈N},B={y|y=-x2-2x+18,y∈N},则A∩B中所有元素的和是__________。
(一) 选择题
1、定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上单调递增,设a=f(3),b=f(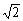 ),c=f(2),则a,b,c大小关系是
),c=f(2),则a,b,c大小关系是
A、a>b>c B、a>c>b C、b>c>a D、c>b>a
2、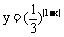 的单调减区间是
的单调减区间是
A、(-∞,1) B、(1,+∞) C、(-∞,-1)∪(1,+∞) D、(-∞,+∞)
3、函数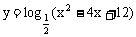 的值域为
的值域为
A、 (-∞,3] B、(-∞,-3] C、(-3,+∞) D、(3,+∞)
4、函数y=log2|ax-1|(a≠b)的图象的对称轴是直线x=2,则a等于
A、  B、
B、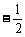 C、2
D、-2
C、2
D、-2
5、有长度为24的材料用一矩形场地,中间加两隔墙,要使矩形的面积最大,则隔壁的长度为
A、 3 B、4 C、6 D、12
1、 深化对函数概念(解析式、定义域、值域)、分段函数
(1)函数的定义域、值域
1.(2009福建卷文)下列函数中,与函数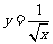 有相同定义域的是A
有相同定义域的是A
A .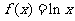 B.
B.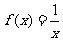 C.
C. 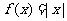 D.
D.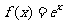
2.(2009江西卷理)函数 的定义域为C
的定义域为C
A.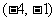 B.
B.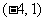 C.
C.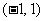 D.
D.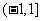
3.(2009安徽卷理)已知函数 在R上满足
在R上满足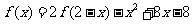 ,则曲线
,则曲线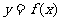 在点
在点 处的切线方程是(A) A(((
处的切线方程是(A) A(((
(A)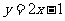 (B)
(B)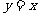 (C)
(C)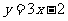 (D)
(D)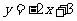
(2)函数的解析式
4(2007山东理6)给出下列三个等式: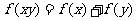 ,
,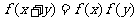 ,
, 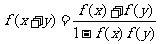 ,下列函数中不满足其中任何一个等式的是( B )
,下列函数中不满足其中任何一个等式的是( B )
A.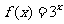 B.
B.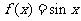 C.
C.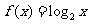 D.
D.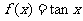
5. (2009辽宁卷文)已知函数 满足:x≥4,则
满足:x≥4,则 =
=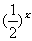 ;当x<4时
;当x<4时 =
=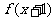 ,则
,则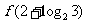 =A
=A
(A)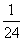 (B)
(B)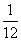 (C)
(C)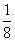 (D)
(D)
(3)分段函数
6.(2009北京文)已知函数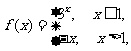 若
若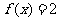 ,则
,则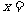 .
.
[答案]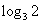
7. (2009山东卷文)定义在R上的函数f(x)满足f(x)= 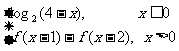 ,则f(3)的值为( B
)
,则f(3)的值为( B
)
A.-1 B. -2 C.1 D. 2
8.(2009天津卷文)设函数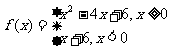 则不等式
则不等式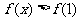 的解集是( A )
的解集是( A )
A 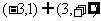 B
B 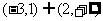
C 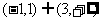 D
D 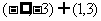
2、函数的图像、性质(单调性、最值、奇偶性、周期性)
(1)函数的图像
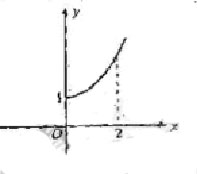
9.(2009福建卷文)定义在R上的偶函数 的部分图像如右图所示,则在
的部分图像如右图所示,则在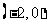 上,下列函数中与
上,下列函数中与 的单调性不同的是(C)
的单调性不同的是(C)
 A.
A.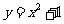
B. 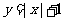
C. 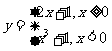
D.
10.(2009北京文)为了得到函数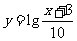 的图像,只需把函数
的图像,只需把函数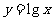 的图像上所有的点 ( C
)
的图像上所有的点 ( C
)
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
11.(2009山东卷文)函数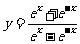 的图像大致为( A ).
的图像大致为( A ).
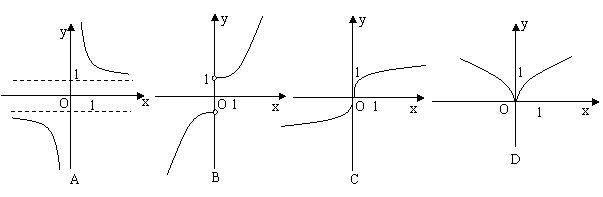

(2)函数的性质(单调性、最值、奇偶性、周期性)
12.(2009重庆卷理)若 是奇函数,则
是奇函数,则
[答案]
13.(2009福建卷理)下列函数 中,满足“对任意
中,满足“对任意 ,
,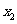
 (0,
(0, ),当
),当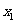 <
<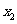 时,都有
时,都有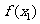 >
>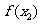 的是(A)
的是(A)
A. =
=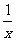 B.
B.  =
=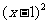 C .
C . =
=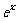 D
D 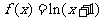
14.(2009辽宁卷文)已知偶函数 在区间
在区间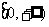 单调增加,则满足
单调增加,则满足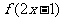 <
<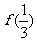 的x 取值范围是(A)
的x 取值范围是(A)
(A)(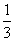 ,
,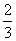 ) (B) [
) (B) [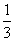 ,
,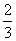 ) (C)(
) (C)(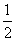 ,
,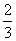 ) (D) [
) (D) [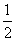 ,
,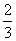 )
)
15.(2009陕西卷文)定义在R上的偶函数 满足:对任意的
满足:对任意的 ,有
,有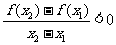 .则(A)
.则(A)
(A)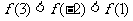 (B)
(B) 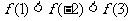
(C) 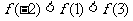 (D)
(D)
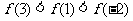
16.(2009福建卷文)若函数 的零点与
的零点与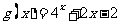 的零点之差的绝对值不超过0.25, 则
的零点之差的绝对值不超过0.25, 则 可以是(A)
可以是(A)
A. 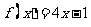 B.
B.
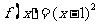
C.  D.
D.
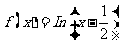
17.(2009山东卷理)定义在R上的函数f(x)满足f(x)= 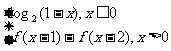 ,则f(2009)的值为( C )
,则f(2009)的值为( C )
A.-1 B. 0 C.1 D. 2
(12)(2009宁夏文12)用min{a,b,c}表示a,b,c三个数中的最小值(C)
设f(x)=min{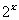 , x+2,10-x} (x
, x+2,10-x} (x 0),则f(x)的最大值为
0),则f(x)的最大值为
(A)4 (B)5 (C)6 (D)7
18.(09山东文)已知定义在R上的奇函数 ,满足
,满足 ,且在区间[0,2]上是增函数,则( D ).
,且在区间[0,2]上是增函数,则( D ).
A. B.
B. 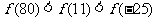
C. 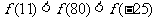 D.
D.
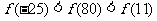
3、基本初等函数(指、对、幂函数)的性质及应用
(1)基本初等函数
19.(2007山东理4)设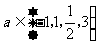 ,则使函数
,则使函数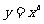 的定义域为
的定义域为 且为奇函数的所有
且为奇函数的所有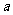 值为( )
值为( )
A. ,
,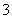 B.
B. ,
, C.
C.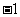 ,
,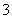 D.
D.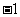 ,
, ,
,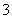
20.(2007山东文14)函数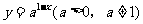 的图象恒过定点
的图象恒过定点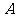 ,若点
,若点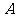 在直线
在直线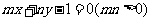 上,则
上,则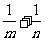 的最小值为
.
的最小值为
.
21.(2009天津卷文)设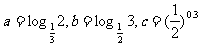 ,则(B)
,则(B)
A a<b<c B a<c<b C b<c<a D b<a<c
22.(2009湖南卷理)若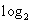 a<0,
a<0,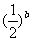 >1,则
(D)
>1,则
(D)
A.a>1,b>0 B.a>1,b<0 C. 0<a<1, b>0 D. 0<a<1, b<0
9.(2009江苏卷)已知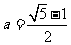 ,函数
,函数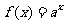 ,若实数
,若实数 、
、 满足
满足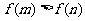 ,则
,则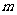 、
、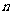 的大小关系为 .
的大小关系为 .
[答案]m<n
23.(2009江苏卷)已知集合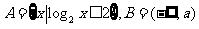 ,若
,若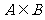 则实数
则实数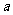 的取值范围是
的取值范围是 ,其中
,其中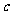 = .
= .
[答案]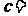 4
4
(2)函数的零点
24.(2009福建卷文)若函数 的零点与
的零点与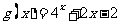 的零点之差的绝对值不超过0.25, 则
的零点之差的绝对值不超过0.25, 则 可以是A
可以是A
A. 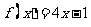 B.
B. 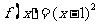
C.  D.
D.
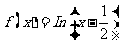
25.(2009山东卷文)若函数f(x)=a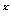 -x-a(a>0且a
-x-a(a>0且a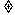 1)有两个零点,则实数a的取值范围是 .
1)有两个零点,则实数a的取值范围是 .
[答案]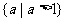
4函数模型及其应用
26、某工厂今年1月,2月,3月生产某产品分别为1万件,1.2万件,1.3万件,为了估测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量y与月份数x的关系,模拟函数可选用y=abx+c(其中a,b,c为常数)或二次函数,已知4月份该产品的产量为1.37万件,请问用哪个函数作为模拟函数较好?并说明理由。
分析:
设f(x)=px2+qx+r(p≠0)
则
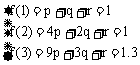
∴
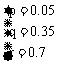
∴ f(4)=-0.05×42+0.35×4+0.7=1.3
设g(x)=abx+c
则
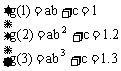
∴
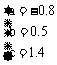
∴ g(4)=-0.8×0.54+1.4=1.35
∵ |1.35-1.37|<|1.3-1.37|
∴ 选用y=-0.8×(0.5)x+1.4作为模拟函数较好。
27.(2009湖南卷理)(本小题满分13分)
某地建一座桥,两端的桥墩已建好,这两墩相距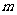 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为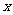 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为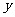 万元。
万元。
(Ⅰ)试写出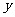 关于
关于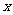 的函数关系式;
的函数关系式;
(Ⅱ)当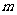 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使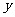 最小?
最小?
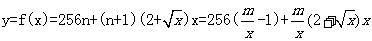
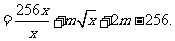
 在
在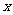 =64处取得最小值,此时,
=64处取得最小值,此时,
5导数的计算、几何意义
28.(2009福建卷理)若曲线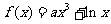 存在垂直于
存在垂直于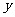 轴的切线,则实数
轴的切线,则实数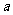 取值范围是_____________.
取值范围是_____________.
[答案]:
29.(2009宁夏海南卷文)曲线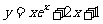 在点(0,1)处的切线方程为
。
在点(0,1)处的切线方程为
。
[答案]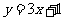
30.(2009全国卷Ⅰ理) 已知直线y=x+1与曲线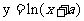 相切,则α的值为( B
)
相切,则α的值为( B
)
(A)1 (B)2 (C) -1 (D)-2
31.(2009湖南卷文)若函数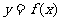 的导函数在区间
的导函数在区间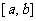 上是增函数,
上是增函数,
则函数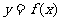 在区间
在区间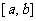 上的图象可能是[ A ]
上的图象可能是[ A ]
|
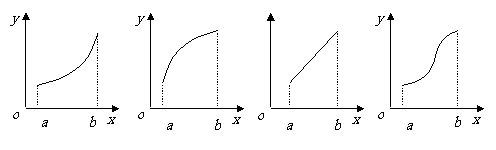

A . B. C. D.
48.(2009陕西卷文)设曲线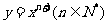 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为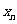 ,则
,则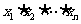 的值为(
B )
的值为(
B )
(A) 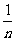 (B)
(B)
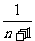 (C)
(C)
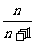 (D)
1
(D)
1
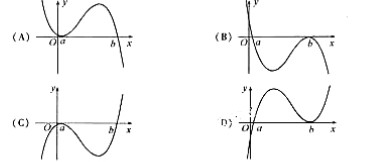
33.(2009安徽卷理)设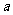 <b,函数
<b,函数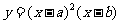 的图像可能是(C) )
的图像可能是(C) )
6函数与导数的综合应用
(1)导数与不等式
34.(2008四川卷22).(本小题满分14分)
已知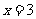 是函数
是函数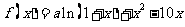 的一个极值点。
的一个极值点。
(Ⅰ)求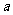 ;
;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若直线 与函数
与函数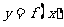 的图象有3个交点,求
的图象有3个交点,求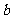 的取值范围。
的取值范围。
[解]:(Ⅰ)因为
所以
因此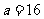
(Ⅱ)由(Ⅰ)知,
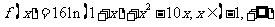
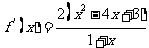
当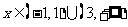 时,
时,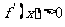
当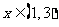 时,
时,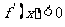
所以 的单调增区间是
的单调增区间是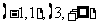
 的单调减区间是
的单调减区间是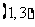
(Ⅲ)由(Ⅱ)知, 在
在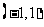 内单调增加,在
内单调增加,在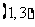 内单调减少,在
内单调减少,在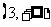 上单调增加,且当
上单调增加,且当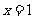 或
或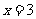 时,
时,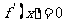
所以 的极大值为
的极大值为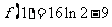 ,极小值为
,极小值为
因此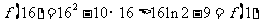

所以在 的三个单调区间
的三个单调区间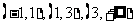 直线
直线 有
有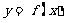 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当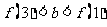
因此,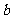 的取值范围为
的取值范围为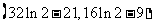 。
。
(2)导数与函数性质
35.(2009年广东卷文)(本小题满分14分)
已知二次函数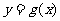 的导函数的图像与直线
的导函数的图像与直线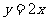 平行,且
平行,且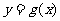 在
在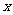 =-1处取得最小值m-1(m
=-1处取得最小值m-1(m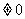 ).设函数
).设函数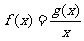 ,若曲线
,若曲线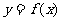 上的点P到点Q(0,2)的距离的最小值为
上的点P到点Q(0,2)的距离的最小值为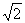 ,求m的值
,求m的值
[解析](1)设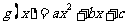 ,则
,则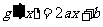 ;
;
又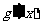 的图像与直线
的图像与直线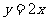 平行
平行 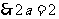
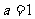
又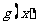 在
在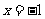 取极小值,
取极小值, 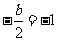 ,
, 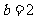
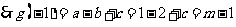 ,
, 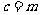 ;
;
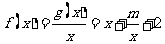 , 设
, 设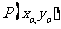
则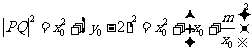

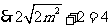
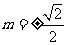 ;21世纪教育网
;21世纪教育网
36.(2009浙江文)(本题满分15分)已知函数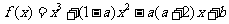
 .
.
(I)若函数 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,求
,求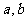 的值;
的值;
(II)若函数 在区间
在区间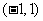 上不单调,求
上不单调,求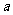 的取值范围.
的取值范围.
解析 (Ⅰ)由题意得
又 ,解得
,解得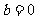 ,
,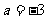 或
或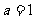
(Ⅱ)函数 在区间
在区间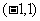 不单调,等价于
不单调,等价于
导函数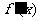 在
在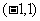 既能取到大于0的实数,又能取到小于0的实数
既能取到大于0的实数,又能取到小于0的实数
即函数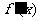 在
在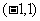 上存在零点,根据零点存在定理,有
上存在零点,根据零点存在定理,有
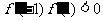 , 即:
, 即: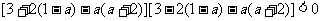
整理得: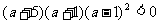 ,解得
,解得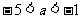
37.(2009北京文)(本小题共14分)
设函数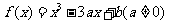 .
.
(Ⅰ)若曲线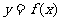 在点
在点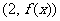 处与直线
处与直线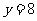 相切,求
相切,求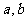 的值;
的值;
(Ⅱ)求函数 的单调区间与极值点.
的单调区间与极值点.
解析 本题主要考查利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力.
(Ⅰ)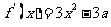 ,
,
∵曲线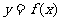 在点
在点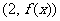 处与直线
处与直线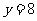 相切,
相切,
∴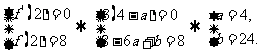
(Ⅱ)∵ ,
,
当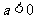 时,
时,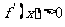 ,函数
,函数 在
在 上单调递增,
上单调递增,
此时函数 没有极值点.
没有极值点.
当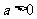 时,由
时,由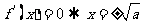 ,
,
当 时,
时,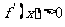 ,函数
,函数 单调递增,
单调递增,
当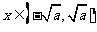 时,
时,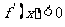 ,函数
,函数 单调递减,
单调递减,
当 时,
时,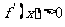 ,函数
,函数 单调递增,
单调递增,
∴此时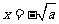 是
是 的极大值点,
的极大值点,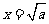 是
是 的极小值点
的极小值点
38.(2009辽宁卷文)(本小题满分12分)
设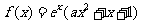 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。
(I) 求a的值,并讨论f(x)的单调性;
(II)
证明:当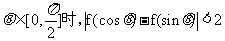
解析 (Ⅰ)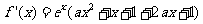 .有条件知,
.有条件知,
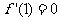 ,故
,故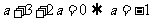 .
………2分 于是
.
………2分 于是 .
.
故当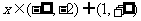 时,
时,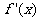 <0;
<0;
当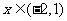 时,
时,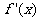 >0.
>0.
从而 在
在 ,
, 单调减少,在
单调减少,在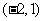 单调增加. ………6分
单调增加. ………6分
(Ⅱ)由(Ⅰ)知 在
在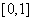 单调增加,故
单调增加,故 在
在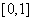 的最大值为
的最大值为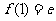 ,
,
最小值为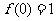 .
.
从而对任意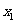 ,
,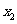
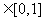 ,有
,有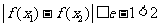 .
………10分
.
………10分
而当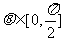 时,
时,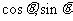
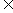
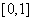 .
.
从而  ………12分
………12分
(3)导数与数列
39(2008福建理18)(本小题满分12分)已知函数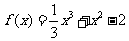 .
.
(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点 (n∈N*)在函数
(n∈N*)在函数
y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(Ⅱ)求函数f(x)在区间(a-1,a)内的极值.
(19)本小题主要考查函数极值、等差数列等基本知识,考查分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.满分12分.
(Ⅰ)证明:因为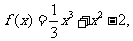 所以
所以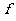 ′(x)=x2+2x,
′(x)=x2+2x,
由点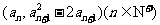 在函数y=f′(x)的图象上,
在函数y=f′(x)的图象上,
又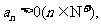 所以
所以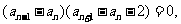
所以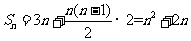 ,又因为
,又因为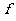 ′(n)=n2+2n,所以
′(n)=n2+2n,所以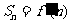 ,
,
故点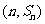 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.
(Ⅱ)解: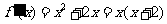 ,
,
由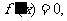 得
得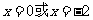 .
.
当x变化时,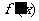 ﹑
﹑ 的变化情况如下表:
的变化情况如下表:
|
x |
(-∞,-2) |
-2 |
(-2,0) |
0 |
(0,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
注意到 ,从而
,从而
①当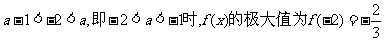 ,此时
,此时 无极小值;
无极小值;
②当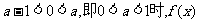 的极小值为
的极小值为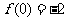 ,此时
,此时 无极大值;
无极大值;
③当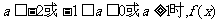 既无极大值又无极小值.
既无极大值又无极小值.
巩固练习
6、主要思想方法:数形结合,分类讨论,函数方程,化归等。
5、导数
(1) 了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等)。掌握函数在某一点处的导数的定义和导数的几何意义。理解导函数的概念。
(2)熟记基本导数公式(c,xm(m为有理数),sinx,cosx,ex,ax,lnx,logax的导数)。掌握两个函数和、差、积、商的求导法则。了解复合函数的求导法则,会求某些简单函数的导数。
(3)了解可导函数的单调性与其导数的关系。了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号)。会求一些实际问题(一般指单峰函数)的最大值和最小值。
4、本单常见的初等函数;一次函数,二次函数,反比例函数,指数函数,对数函数。在具体的对应法则下理解函数的通性,掌握这些具体对应法则的性质。分段函数是重要的函数模型。
对于抽象函数,通常是抓住函数特性是定义域上恒等式,利用赋值法(变量代换法)解题。联系到具体的函数模型可以简便地找到解题思路,及解题突破口。
应用题是函数性质运用的重要题型。审清题意,找准数量关系,把握好模型是解应用题的关键。
2、函数的图象
函数的图象既是函数性质的一个重要方面,又能直观地反映函数的性质,在解题过程中,充分发挥图象的工具作用。
图象作法:①描点法;②图象变换。应掌握常见的图象变换。
2、函数的通性
(1)奇偶性:函数定义域关于原点对称是判断函数奇偶性的必要条件,在利用定义判断时,应在化简解析式后进行,同时灵活运用定义域的变形,如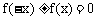 ,
,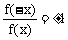 (f(x)≠0)。
(f(x)≠0)。
奇偶性的几何意义是两种特殊的图象对称。
函数的奇偶性是定义域上的普遍性质,定义式是定义域上的恒等式。
利用奇偶性的运算性质可以简化判断奇偶性的步骤。
(2)单调性:研究函数的单调性应结合函数单调区间,单调区间应是定义域的子集。
判断函数单调性的方法:①定义法,即比差法;②图象法;③单调性的运算性质(实质上是不等式性质);④复合函数单调性判断法则。
函数单调性是单调区间上普遍成立的性质,是单调区间上恒成立的不等式。
函数单调性是函数性质中最活跃的性质,它的运用主要体现在不等式方面,如比较大小,解抽象函数不等式等。
(3)周期性:周期性主要运用在三角函数及抽象函数中,是化归思想的重要手段。
求周期的重要方法:①定义法;②公式法;③图象法;④利用重要结论:若函数f(x)满足f(a-x)=f(a+x),f(b-x)=f(b+x),a≠b,则T=2|a-b|。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com