
21. 设等比数列的通项为
设等比数列的通项为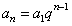 因
因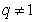 所以
所以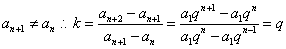
所以公比不为1的等比数列是等差比数列,且公比等于公差比.
(2)由
由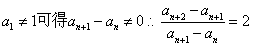 故数列{
故数列{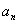 }是等差比数列.
}是等差比数列.
由
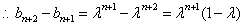
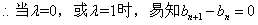
此时数列{ }不是等差比数列
}不是等差比数列
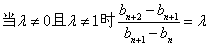 .此时数列{
.此时数列{ }是等差比数列.
}是等差比数列.
(3) 数列{ }是公差比为k的等差比数列,
}是公差比为k的等差比数列,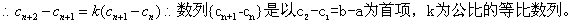
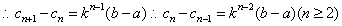
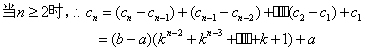
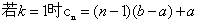
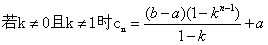
综上可知: 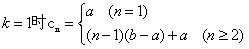
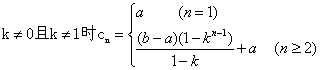
18. 19.
19.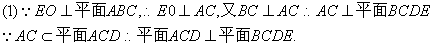
 方法一
方法一
 方法二:
方法二:
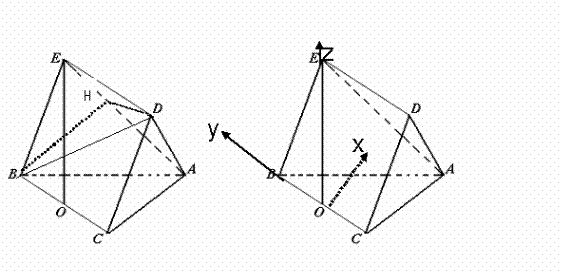
因为EO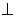 平面ABC,所以以O 为原点,过O平行于AC的直线为x轴,BC 所在直线为轴y,OE所在直线为z轴,建立空间直角坐标系。
平面ABC,所以以O 为原点,过O平行于AC的直线为x轴,BC 所在直线为轴y,OE所在直线为z轴,建立空间直角坐标系。
设BC=CA=BE=1,由题意可知:B(0,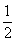 ,0),E(0,0,
,0),E(0,0,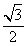 )D(0,-1,
)D(0,-1,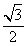 )A(1,-
)A(1,-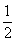 ,0)
,0)
设平面ABE的一个法向量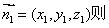

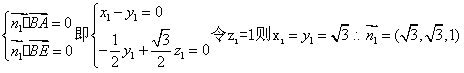
设平面ADE的一个法向量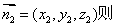

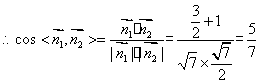
所以平面ABE与平面ADE所成的锐角的余弦值为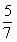 。
。
20解:(I)如图, ,
,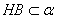 ,
,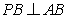 ,
,
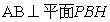 所以
所以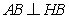 ,所以
,所以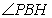 是
是
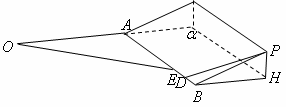 山坡与
山坡与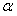 所成二面角的平面角,则
所成二面角的平面角,则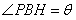 ,
,
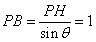 .设
.设 ,
,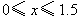 .
.
则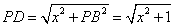
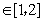 .
.
记总造价为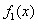 万元,
万元,
据题设有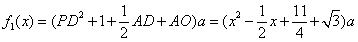
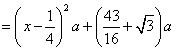
当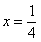 ,即
,即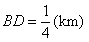 时,总造价
时,总造价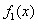 最小.
最小.
(II)设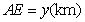 ,
,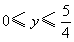 ,总造价为
,总造价为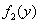 万元,根据题设有
万元,根据题设有
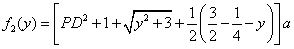
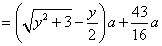 .
.
则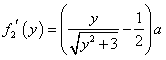 ,由
,由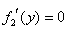 ,得
,得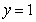 .
.
当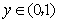 时,
时, ,
,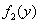 在
在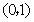 内是减函数;
内是减函数;
当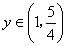 时,
时,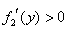 ,
,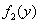 在
在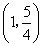 内是增函数.
内是增函数.
故当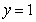 ,即
,即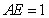 (km)时总造价
(km)时总造价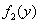 最小,且最小总造价为
最小,且最小总造价为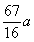 万元.
万元.
(III)解法一:不存在这样的点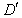 ,
,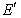 .
.
事实上,在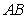 上任取不同的两点
上任取不同的两点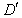 ,
,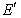 .为使总造价最小,
.为使总造价最小,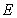 显然不能位于
显然不能位于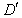 与
与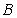 之间.故可设
之间.故可设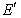 位于
位于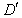 与
与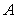 之间,且
之间,且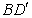 =
=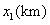 ,
,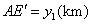 ,
,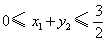 ,总造价为
,总造价为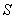 万元,则
万元,则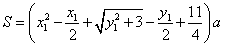 .类似于(I)、(II)讨论知,
.类似于(I)、(II)讨论知,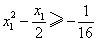 ,
,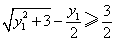 ,当且仅当
,当且仅当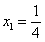 ,
,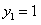 同时成立时,上述两个不等式等号同时成立,此时
同时成立时,上述两个不等式等号同时成立,此时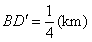 ,
,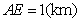 ,
, 取得最小值
取得最小值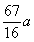 ,点
,点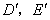 分别与点
分别与点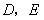 重合,所以不存在这样的点
重合,所以不存在这样的点 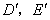 ,使沿折线
,使沿折线 修建公路的总造价小于(II)中得到的最小总造价.
修建公路的总造价小于(II)中得到的最小总造价.
解法二:同解法一得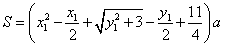
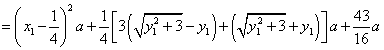
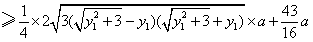
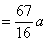 .
.
当且仅当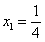 且
且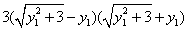 ,即
,即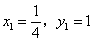 同时成立时,
同时成立时,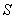 取得最小值
取得最小值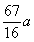 ,以上同解法一.
,以上同解法一.
17.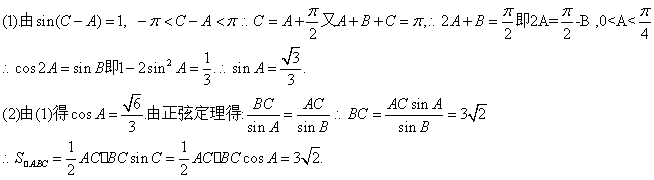
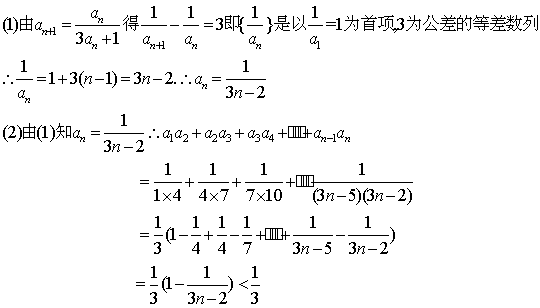
16.
15. (-3,-2)
13. 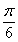 .
14. ①②③
.
14. ①②③
11. (4,6) 12. 2236
21.(本小题满分13分)在数列{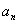 }中,如果对任意
}中,如果对任意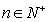 都有
都有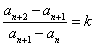 (k是不为零的常数),则称{
(k是不为零的常数),则称{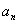 }为等差比数列,k称为公差比.
}为等差比数列,k称为公差比.
(1)证明:公比不为1的等比数列是等差比数列,且公比等于公差比;
(2) 判断两个数列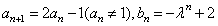 是否为等差比数列;
是否为等差比数列;
(3)若数列{ }是首项为
}是首项为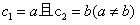 ,公差比为k的等差比数列,
,公差比为k的等差比数列,
求{ }的通项公式。
}的通项公式。
衡阳市八中2010届高三第四次月考答题卷
数学(理科)
20. (本小题满分13分)
如图,某地为了开发旅游资源,欲修建一条连接风景点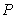 和居民区
和居民区 的公路,点
的公路,点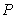 所在的山坡面与山脚所在水平面
所在的山坡面与山脚所在水平面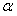 所成的二面角为
所成的二面角为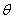 (
(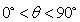 ),且
),且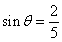 ,点
,点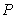 到平面
到平面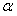 的距离
的距离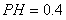 (km).沿山脚原有一段笔直的公路
(km).沿山脚原有一段笔直的公路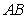 可供利用.从点
可供利用.从点 到山脚修路的造价为
到山脚修路的造价为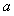 万元/km,原有公路改建费用为
万元/km,原有公路改建费用为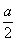 万元/km.当山坡上公路长度为
万元/km.当山坡上公路长度为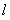 km(
km(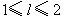 )时,其造价为
)时,其造价为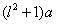 万元.已知
万元.已知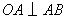 ,
,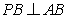 ,
,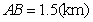 ,
,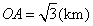 .
.
(I)在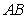 上求一点
上求一点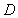 ,使沿折线
,使沿折线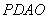 修建公路的总造价最小;
修建公路的总造价最小;
(II) 对于(I)中得到的点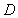 ,在
,在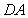 上求一点
上求一点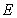 ,使沿折线
,使沿折线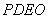 修建公路的总造价最小.
修建公路的总造价最小.
(III)在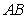 上是否存在两个不同的点
上是否存在两个不同的点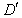 ,
,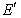 ,使沿折线
,使沿折线 修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.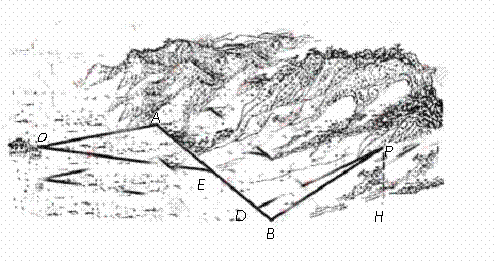
19. (本小题满分13分)
(本小题满分13分)
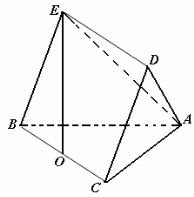
如图,在多面体ABCDE中,底面△ABC为等腰直角三角形,且∠ACB=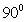 ,侧面BCDE是棱形,O点是BC 的中点,EO
,侧面BCDE是棱形,O点是BC 的中点,EO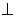 平面ABC
平面ABC
(1)求证:平面ACD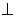 平面BCDE;
平面BCDE;
(2)求平面ABE与平面ADE所成锐角的余弦值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com