
14.(2010广东理)1.若集合A={ -2<
-2<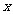 <1},B={
<1},B={ 0<
0<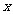 <2}则集合A ∩ B=( )
<2}则集合A ∩ B=( )
A. { -1<
-1<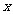 <1}
B. {
<1}
B. { -2<
-2<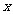 <1}
<1}
C. { -2<
-2<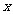 <2}
D. {
<2}
D. { 0<
0<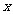 <1}
<1}
答案 D.
[解析] .
.
13.(2010天津理)(9)设集合A= 若A
若A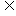 B,则实数a,b必满足
B,则实数a,b必满足
(A) (B)
(B)
(C) (D)
(D)
答案 D
[解析]本题主要考查绝对值不等式的解法与几何与结合之间的关系,属于中等题。
A={x|a-1<x<a+1},B={x|x<b-2或x>b+2}
因为A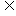 B,所以a+1
B,所以a+1 b-2或a-1
b-2或a-1 b+2,即a-b
b+2,即a-b -3或a-b
-3或a-b 3,即|a-b|
3,即|a-b| 3
3
[温馨提示]处理几何之间的子集、交、并运算时一般利用数轴求解。
12.(2010天津文)(7)设集合
 则实数a的取值范围是
则实数a的取值范围是
(A) (B)
(B)
(C) (D)
(D)
答案 C
[解析]本题主要考查绝对值不等式的基本解法与集合交集的运算,属于中等题。
由|x-a|<1得-1<x-a<1,即a-1<x<a+1.如图 由图可知a+1≦1或a-1≧5,所以a≦0或a≧6.
由图可知a+1≦1或a-1≧5,所以a≦0或a≧6.
[温馨提示]不等式型集合的交、并集通常可以利用数轴进行,解题时注意验证区间端点是否符合题意。
11.(2010北京理)(1) 集合 ,则
,则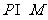 =
=
(A) {1,2} (B) {0,1,2} (C){x|0≤x<3} (D) {x|0≤x≤3}
答案:B
10.(2010北京文)⑴ 集合 ,则
,则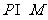 =
=
(A) {1,2} (B) {0,1,2} (C){1,2,3} (D){0,1,2,3}
答案:B
9.(2010山东文)(1)已知全集 ,集合
,集合 ,则
,则 =
=
A.  B.
B. 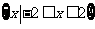
C. D.
D. 
答案:C
8.(2010浙江文)(1)设 则
则
(A) (B)
(B)
(C) (D)
(D)
答案 D
解析: ,故答案选D,本题主要考察了集合的基本运算,属容易题
,故答案选D,本题主要考察了集合的基本运算,属容易题
7.(2010安徽文)(1)若A= ,B=
,B= ,则
,则 =
=
(A)(-1,+∞) (B)(-∞,3) (C)(-1,3) (D)(1,3)
答案 C
[解析] ,
, ,故选C.
,故选C.
[方法总结]先求集合A、B,然后求交集,可以直接得结论,也可以借助数轴得交集.
6.(2010江西理)2.若集合 ,
, ,则
,则 =( )
=( )
A.  B.
B.

C.  D.
D.

答案 C
[解析]考查集合的性质与交集以及绝对值不等式运算。常见的解法为计算出集合A、B; ,
, ,解得
,解得 。在应试中可采用特值检验完成。
。在应试中可采用特值检验完成。
5.(2010全国卷2文)

(A) (B)
(B)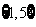 (C)
(C) (D)
(D)
答案C
解析:本题考查了集合的基本运算. 属于基础知识、基本运算的考查.
∵ A={1,3}。B={3,5},∴  ,∴
,∴ 故选 C .
故选 C .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com