
2、下列各组词语中,没有错别字的一组是( )
A、 干燥 飘零 远见卓识 酩酊大醉 逝者如斯夫
B、 萧瑟 洗炼 再接再励 感恩带德 松柏之后彫也
C、 妨碍 婉惜 一筹莫展 套语烂调 御六气之辨
D、 炫耀 喟叹 仗义直言 运筹帷幄 臣生当陨首
1、下列各组词语中,加点字读音全都正确的一项上( )
A、赍发(jī) 迤逦(lǐ) 糍粑(cī ) 锱铢必较(zhī zhū)
B、傩送(nuó) 潦水(liáo) 怃然(wǔ) 闭目塞听(sè)
C、鲱鱼(fēi) 付梓(zǐ) 泠然(lěng) 不揣冒昧(chuǎi)
D、流憩(qì) 畏葸(xǐ) 木铎(duó) 不落言筌(quán)
 b)∈M,且对M中的其它元素(c,d),总有c≥a,则a=____.
b)∈M,且对M中的其它元素(c,d),总有c≥a,则a=____.
分析:读懂并能揭示问题中的数学实质,将是解决该问题的突破口.怎样理解“对M中的其它元素(c,d),总有c≥a”?M中的元素又有什么特点?
解:依题可知,本题等价于求函数x=f(y)=(y+3)·|y-1|+(y+3)


 [来源:][来源:学*科*网]
[来源:][来源:学*科*网]

(2)当1≤y≤3时,
所以当y=1时, = 4.
= 4.

简评:题设条件中出现集合的形式,因此要认清集合元素的本质属性,然后结合条件,揭示
其数学实质.即求集合M中的元素满足关系式
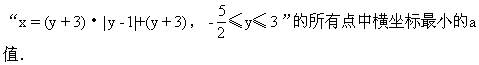
例2.已知非负实数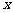 ,
, 满足
满足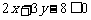 且
且 ,则
,则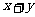 的最大值是( )
的最大值是( )
A. B.
B.
 C.
C.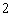 D.
D. 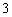
解:画出图象,由线性规划知识可得,选D
例3.数列 由下列条件确定:
由下列条件确定:
(1)证明:对于 ,
,
(2)证明:对于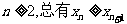 .
.
证明:(1)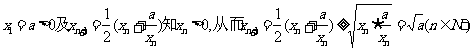
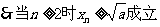
(2)当 时,
时,
= 。
。
例4.解关于 的不等式:
的不等式: [来源:]
[来源:]
分析:本例主要复习含绝对值不等式的解法,分类讨论的思想。本题的关键不是对参数 进行讨论,而是去绝对值时必须对末知数进行讨论,得到两个不等式组,最后对两个不等式组的解集求并集,得出原不等式的解集。
进行讨论,而是去绝对值时必须对末知数进行讨论,得到两个不等式组,最后对两个不等式组的解集求并集,得出原不等式的解集。
解:当 [来源:]
[来源:]


 。
。
例5.若二次函数y=f(x)的图象经过原点,且1≤f(-1)≤2,3≤f(1)≤4,求f(-2)的范围.
分析:要求f(-2)的取值范围,只需找到含人f (-2)的不等式(组).由于y=f(x)是二次函数,所以应先将f(x)的表达形式写出来.即可求得f(-2)的表达式,然后依题设条件列出含有f(-2)的不等式(组),即可求解.
(-2)的不等式(组).由于y=f(x)是二次函数,所以应先将f(x)的表达形式写出来.即可求得f(-2)的表达式,然后依题设条件列出含有f(-2)的不等式(组),即可求解.
解:因为y=f(x)的图象经过原点,所以可设y=f(x)=ax2+bx.于是

解法一(利用基本不等式的性质)
不等式组(Ⅰ)变形得
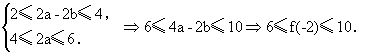
 (Ⅰ)
(Ⅰ)
所以f(-2)的取 值范围是[6,10].
值范围是[6,10].
解法二(数形结合)
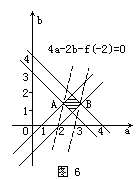
建立直角坐标系aob,作出不等式组(Ⅰ)所表示的区域,如图6中的阴影部分.因为f(-2)=4a-2b,所以4a-2b-f(-2)=0 表示斜率为2的直线系.如图6,当直线4a-2b-f(-2)=0过点A(2,1),B(3,1)时,分别取得f(-2)的最小值6,最大值10.即f(-2)的取值范围是:6≤f(-2)≤10.
表示斜率为2的直线系.如图6,当直线4a-2b-f(-2)=0过点A(2,1),B(3,1)时,分别取得f(-2)的最小值6,最大值10.即f(-2)的取值范围是:6≤f(-2)≤10.
解法三(利用方程的思想)

又f(-2)=4a-2b=3f(-1)+f(1),而
1≤f(-1)≤2,3≤f(1)≤4, ①
所以 3≤3f(-1)≤6. ②
①+②得4≤3f(-1)+f(1)≤10,即6≤f(-2)≤10.
简评:(1)在解不等式时,要求作同解变形.要避免出现以下一种错解:
 2b,8≤4a≤12,-3≤-2b≤-1,所以 5≤f(-2)≤11.
2b,8≤4a≤12,-3≤-2b≤-1,所以 5≤f(-2)≤11.
(2)对这类问题的求解关键一步是,找到f(-2)的数学结构,然后依其数学结构特征,揭示其代数的、几何的本质,利用不等式的基本性质、数形结合、方程等数学思想方法,从不同角度去解决同一问题.若长期这样思考问题,数学的素养一定会迅速提高.
例6.设函数f(x)=ax2+bx+c的图象与两直线y=x,y=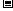 x,均不相交.试证明对一切
x,均不相交.试证明对一切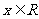 都有
都有 .
.
分析:因为x∈R,故|f(x)|的最小值若存在,则最小值由顶点确定, 故设f(x)=a(x-x0)2+f(x0).
故设f(x)=a(x-x0)2+f(x0).
证明:由题意知,a≠0.设f(x)=a(x-x0)2+f(x0),则
又二次方程ax2+bx+c=±x无实根,故
Δ1=(b+1 )2-4ac<0,Δ2=(b-1)2-4ac<0.
)2-4ac<0,Δ2=(b-1)2-4ac<0.
所以(b+1)2+(b-1)2- 8ac<0,即2b2+2-8ac<0,即b2-4ac<-1,所以|b2-4ac|>1.
8ac<0,即2b2+2-8ac<0,即b2-4ac<-1,所以|b2-4ac|>1.



简评:从上述几个例子可以看出,在证明与二次函数有关的不等式问题时,如果针对题设条件,合理采取二次函数的不同形式,那么我们就找到了一种有效的证明途径.
例7.某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同。为了保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
解:设20 01年末的汽车保有量为
01年末的汽车保有量为 ,以后每年末的汽车保有量依次为
,以后每年末的汽车保有量依次为 ,每年新增汽车
,每年新增汽车 万辆。由题意得
万辆。由题意得


4.根据题目结构特点,执果索因,往往是有效的思维方法。
3.不等式证明方法有多种,既要注意到各种证法的适用范围,又要注意在掌握常规证法的基础上,选用一些特殊技巧。如运用放缩法证明不等式时要注意调整放缩的度。
2.解含参数不等式时,要特别注意数形结合思想,函数与方程思想,分类讨论思想的录活运用。
1.解不等式的基本思想是转化、化归,一般都转化为最简单的一元一次不等式(组)或一元二次不等式(组)来求解,。
7.通过不等式的基本知识、基本方法在代数 、三角函数、数列、复数、立体几何、解析几何等各部分知识中
、三角函数、数列、复数、立体几何、解析几何等各部分知识中 的应用,深化数学知识间的融汇贯通,从而提高分析问题解决问题的能力.在应用不等式的基本知识、
的应用,深化数学知识间的融汇贯通,从而提高分析问题解决问题的能力.在应用不等式的基本知识、 方法、思想解决问题的过程中,提高学生数学素质及创新意识.
方法、思想解决问题的过程中,提高学生数学素质及创新意识.
6.不等式应用问题体现了一定的综合性.这类问题大致可以分为两类:一类是建立不等式、解不等式;另一类是建 立函数式求最大值或最小值.利用平均值不等式求函数的最值时,要特别注意“正数、定值和相等”三个条件缺一不可,有时需要适当拼凑,使之符合这三个条件.利用不等式解应用题的基本步骤:1.审题,2.建立不等式模型,3.解数学问题,4.作答。
立函数式求最大值或最小值.利用平均值不等式求函数的最值时,要特别注意“正数、定值和相等”三个条件缺一不可,有时需要适当拼凑,使之符合这三个条件.利用不等式解应用题的基本步骤:1.审题,2.建立不等式模型,3.解数学问题,4.作答。
5.证明不等式的方法多样,内容丰富、技巧性较强.在证明不等式前,要依据题设和待证不等式的结构特点、内在联系,选择适当的证明方法.通过等式或不等式的运算,将待证的不等式化为明显的、熟知的不等式,从而使原不等式得到证明;反之亦可从明显的、熟知的不 等式入手,经过一系列的运算而导出待证的不等式,前者是“执果索因”,后者是“由因导果”,为沟通联系的途径,证明时往往联合使用分析综合法,两面夹击,相辅相成,达到欲证的目的.
等式入手,经过一系列的运算而导出待证的不等式,前者是“执果索因”,后者是“由因导果”,为沟通联系的途径,证明时往往联合使用分析综合法,两面夹击,相辅相成,达到欲证的目的.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com