
(13)  (14) 2
(15)
(14) 2
(15)  (16)
(16) 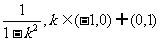
(1)A (2)B (3)A (4)A (5)C (6)D (7)C (8)B (9)C (10)B (11)D (12)D
(八)圆锥曲线 答案

(18) (本小题满分10分)
某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到该巨响的时间比其他两观测点晚4s.已知各观测点到该中心的距离都是1020m.试确定该巨响发生的位置。(假定当时声音传播的速度为340m/s;相关各点均在同一平面上)
(19)(本小题满分10分)
已知抛物线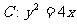 ,顶点为O,动直线
,顶点为O,动直线 与抛物线
与抛物线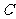 交于
交于 、
、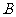 两点
两点
(I)求证: 是一个与
是一个与 无关的常数;
无关的常数;
(II)求满足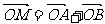 的点
的点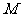 的轨迹方程。
的轨迹方程。
(20)(本小题满分12分)
已知向量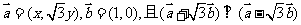 .
.
(Ⅰ)求点 的轨迹C的方程;
的轨迹C的方程;
(Ⅱ)设曲线C与直线 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点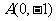 ,当
,当 时,求实数
时,求实数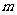 的取值范围。
的取值范围。
(13) 与直线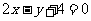 平行的抛物线
平行的抛物线 的切线方程是
。
的切线方程是
。
(14)
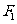 、
、 是椭圆C:
是椭圆C: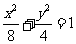 的焦点,在C上满足
的焦点,在C上满足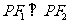 的点
的点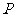 的个数为 。
的个数为 。
(15) 函数 的图象是平面上到两定点的距离之差的绝对值等于定长的点的轨迹,则这个定长为
。
的图象是平面上到两定点的距离之差的绝对值等于定长的点的轨迹,则这个定长为
。
(16) 过点 的直线
的直线 与抛物线
与抛物线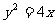 交于
交于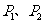 两点,记线段
两点,记线段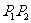 的中点为
的中点为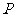 ,过点
,过点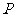 和这个抛物线的焦点
和这个抛物线的焦点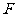 的直线为
的直线为 ,
, 的斜率为
的斜率为 ,则直线
,则直线 的斜率与直线
的斜率与直线 的斜率之比可表示为
的斜率之比可表示为 的函数
的函数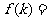 __ .
__ .
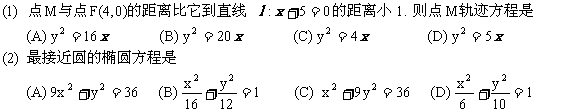
(3) 若椭圆的离心率为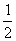 ,左焦点到相应的左顶点的距离为1,则椭圆的长轴长是
,左焦点到相应的左顶点的距离为1,则椭圆的长轴长是
(A)4
(B) (C) 2 (D)
(C) 2 (D) 
 (6) 若抛物线
(6) 若抛物线 与
与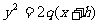 有共同焦点,则
有共同焦点,则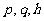 的关系是
的关系是
(A) (B)
(B) (C)
(C)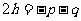 (D)
(D)
(7) 过双曲线的一个焦点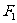 作垂直于实轴的弦
作垂直于实轴的弦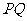 ,
,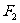 是另一个焦点,若
是另一个焦点,若 。则此双曲线的离心率为
。则此双曲线的离心率为
(A)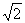 (B)
(B)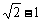 (C)
(C)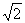 +1 (D)
+1 (D)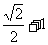
(8) 若椭圆 和双曲线
和双曲线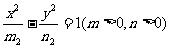 有公共的焦点
有公共的焦点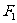 ,
,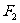 ,
,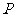 是它们的一个公共点,则
是它们的一个公共点,则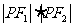 的值是
的值是
(A)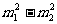 (B)
(B)  (C)
(C) (D)
(D) 
(9) 若焦点坐标为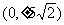 的椭圆与直线
的椭圆与直线 相交所得的弦中点的横坐标是
相交所得的弦中点的横坐标是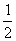 ,则此椭圆的标准方程是
,则此椭圆的标准方程是
(A)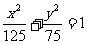 (B)
(B) 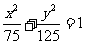 (C)
(C) 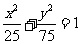 (D)
(D) 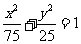
(10) 我国某颗人造地球卫星的运行轨迹是以地心F为一个焦点的椭圆,若它的近地点A距离地面m公里,远地点B距离地面M公里,地球半径为R公里,则该卫星轨迹的离心率e是
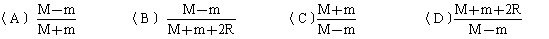
(11) 与双曲线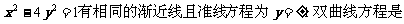

(12) 已知抛物线 上一定点B(-1,0)和两个动点
上一定点B(-1,0)和两个动点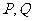 ,当
,当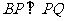 时,点
时,点 的横坐标的取值范围是
的横坐标的取值范围是
(A) (B)
(B) 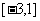
 (C)
(C) 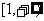 (D)
(D) 
(17)(8分)已知 ,求证
,求证
(18)(10分)解关于x的不等式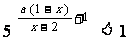
(19)(12分)某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修保养、费用12万元,从第二年开始,每年的维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利?
(3)使用若干年后,对机床的处理方案有两种:(1)当年平均盈利额达到最大值时,以30万元价格处理该机床;(2)当盈利额达到最大值时,以12万元价格处理该机床,问用哪种方案处理较合算?请说明理由.
(20)(12分)已知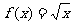 ,g(x)=x+a (a>0)
,g(x)=x+a (a>0)
(1)当a=4时,求 的最小值
的最小值
(2)当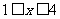 时,不等式
时,不等式 >1恒成立,求a的取值范围.
>1恒成立,求a的取值范围.
(13)已知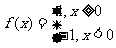 ,则不等式xf(x)+x
,则不等式xf(x)+x 2的解集为
2的解集为
(14)使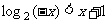 成立的x的范围是
成立的x的范围是
(15)若正数a,b满足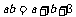 ,则a+b的取值范围是
,则a+b的取值范围是
(16)y=f(x)是R上的减函数,其图象经过点A(0,1)和B(3,-1),则不等式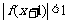 的解集是
.
的解集是
.
(1)不等式 的解集是
的解集是


(2)与不等式 同解的是
同解的是
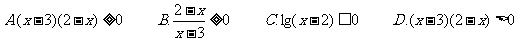
(3)当x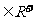 时,下列各函数中,最小值为2的是
时,下列各函数中,最小值为2的是
A. y=x2-2x+4 B. y=x+ C. y=
C. y=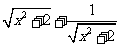 D .y=x+
D .y=x+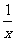
(4)已知a<0,a+b>0,则下列不等式中成立的是
A.ab+a2>0 B.ab-a2>0 C.ab+b2<0 D.ab-b2<0
(5)设f(x)= ,已知f(a)>1,则实数a的范围是
,已知f(a)>1,则实数a的范围是
A. B.
B. C.
C. D.
D.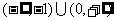
(6)若p,q,m是三个正数,且q<100,现把m增加p%,再把所得的结果减少q%,这样所得的数仍大于m,那么必须且只需
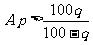 B.
B. C.
C.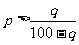 D.p>q
D.p>q
(7)设a1,b1,c1,a2,b2,c2均为非零实数,不等式a1x2+b1x+c1>0,a2x2+b2x+c2>0的解集分别为集合M和N,那么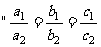 ”是
”是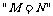 的
的
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件
(8)对一切不等式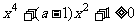 恒成立,则a的取值范围是
恒成立,则a的取值范围是
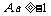 B.
B.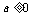 C.
C. D.
D.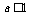
(9)若不等式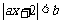 的解集为(-1,2),则实数a等于
的解集为(-1,2),则实数a等于
A.8 B.2 C.-4 D.-8
(10)若关于x的不等式 ,则实数a的取值范围是
,则实数a的取值范围是
A. B.
B. C.(1,2)
D.[1,2]
C.(1,2)
D.[1,2]
(11)已知α、β是关于x的方程x2+mx+m+3=0的两个实根,则α2+β2的最小值是
A.-7 B.2 C.18 D.20
(12)某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下:
|
行业名称 |
计算机 |
机械 |
营销 |
物流 |
贸易 |
|
应聘人数 |
215830 |
200250 |
154676 |
74570 |
65280 |
|
行业名称 |
计算机 |
营销 |
机械 |
建筑 |
化工 |
|
招聘人数 |
124620 |
102935 |
89115 |
76516 |
70436 |
若用同一行业应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形式一定是
A.计算机行业好于化工行业 B.建筑行业好于物流行业
C.机械行业最紧张 D.营销行业比贸易行业紧张
(17)(本小题满分8分)
设平面上有两个向量
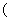 00≤α<3600
00≤α<3600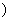 ,
,
(Ⅰ)证明:( )⊥(
)⊥( );
);
(Ⅱ)若 ∥
∥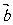 ,求角
,求角 。
。
(18)(本小题满分10分)
已知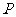 是正方形
是正方形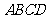 平面外一点,
平面外一点,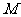 、
、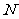 分别是
分别是 、
、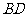 上的点,且
上的点,且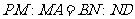
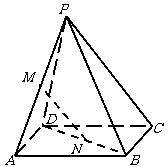
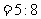 .求证:直线
.求证:直线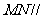 平面
平面
(19)(本小题满分10分)
 甲船由A岛出发向北偏东450的方向作匀速直线航行,速度为15
甲船由A岛出发向北偏东450的方向作匀速直线航行,速度为15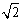 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东450的方向作匀速直线航行,速度为20
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东450的方向作匀速直线航行,速度为20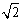 海里/小时(如图)。求两船出发后多长时间相距最近?最近距离为多少海里?
海里/小时(如图)。求两船出发后多长时间相距最近?最近距离为多少海里?
(20)(本小题满分12分)
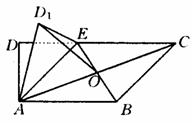 如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上一点,满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点O.
如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上一点,满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点O.
(Ⅰ)试用基向量 表示向量
表示向量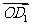 ;
;
(Ⅱ)求异面直线OD1与AE所成的角;
(Ⅲ)判断平面D1AE与平面ABCE是否垂直?并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com