
2.某生活污水有一股臭味,主要含有碎菜叶、碎塑料薄膜、泥沙、氯化钠和碳酸钠等物质。现欲将其经去渣、除臭处理后用作清洗厕所的用水,问:
⑴采用何种操作,可除去污水中的碎菜叶,碎塑料薄膜及泥沙?___________________
⑵用什么物质可除去污水中的臭味?___________________________________________(
⑶把生活污水进行处理再利用的目的是什么?
⑷怎样检验⑴和⑵处理后的水中是否存在氯离子?_______________________________
1.保持洁净安全的生存环境已成为全人类的共识。
(1)为了改善空气质量,必须控制大气中二氧化硫、氮氧化物、烟尘等污染物的排放量。为控制大气中二氧化硫的排放,常采取的措施是对化石燃料进行 。对汽车加装尾气催化净化装置,使其中的有害气体NO、CO转化为无害气体,该反应的化学方程式为 。
(2)获得洁净安全的饮用水是每个人的正常需要。某农村地区为获得饮用水,在将地表水取回家后,常使用漂白粉或漂白精片进行杀菌消毒,其原理可用化学方程式表示为
。
(3)人类产生的垃圾应进行分类回收、集中处理,即便如此,仍会剩余不少垃圾,因此必须对剩余垃圾进一步处理,除卫生填埋外,还有一种能够改变垃圾的组成、结构使其体积减小、充分利用其所具有的能量并使之无害化的处理方式,这种垃圾的处理方式是 ______________。
20. ,∴对称轴为
,∴对称轴为 ,
,
(Ⅰ) ,∴
,∴ 的值域为
的值域为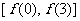 ,即
,即 ;
;
(Ⅰ) a≤-1.5 或 a≥-0.5 8
(Ⅱ) 对称轴
对称轴 ,
,
 , ∵区间
, ∵区间 的中点为
的中点为 ,
,
(1)当 时,
时,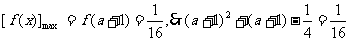 ,
,
 不合);
不合);
(2)当 时,
时, ,
,
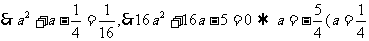 不合);
不合);
综上, .
8
.
8
20.设函数 .
.
(Ⅰ)若定义域为[0,3],求 的值域;
的值域;
(Ⅰ)若f(x)在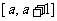 上是是单调函数,求a的取值范围;
上是是单调函数,求a的取值范围;
(Ⅱ)若定义域限制为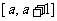 时,
时, 的值域为
的值域为 ,求a的值.
,求a的值.
19. 已知函数f(x)= x∈[2 ,+ ∞)
x∈[2 ,+ ∞)
(1) 当a=1时,判断并证明f(x)的单调性;
(2) 若对任意x∈[2 ,+ ∞), f(x)>0 恒成立,试求实数a的取值范围;
(3) 若f(x)在x∈[2 ,+ ∞) 为增函数,试求实数a的取值范围;
(1) 增函数; 8
(2)a ∈ (-8,+∞ ); 4
(3) a ∈ (-∞,-4] 4
18. 等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域.
等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域.
解 作BH⊥AD,H为垂足,CG⊥AD,G为垂足,
依题意,则有AH= ,AG=
,AG= a.
a.
(1) 当M位于点H的左侧时,N∈AB,
由于AM=x,∠BAD=45°. ∴MN=x. ∴y=S△AMN=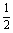 x2(0≤x≤
x2(0≤x≤ ).
).
(2)当M位于HG之间时, 由于AM=x, ∴MN= ,BN=x-
,BN=x- .
.
∴y=S直角梯形AMNB= [x+(x-
[x+(x- )]=
)]=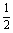 ax-
ax-
(3)当M位于点G的右侧时,
由于AM=x,MN=MD=2a-x. ∴y=S梯形ABCD-S△MDN
=
综上:y=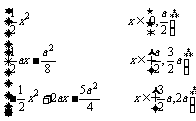 5+5+5
5+5+5
17.已知集合 ,
, ,
,
 ,
, ,且
,且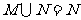 ,求实数
,求实数 的取值范围
的取值范围
解:依题意,
集合 ,
, ,…..4
,…..4
 ,
,
 ,………………4
,………………4
由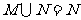 知
知 ,
,
∴实数 的取值范围J
的取值范围J 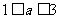
 ……………………………………….6
……………………………………….6
16、 ∵f(m)+f(2m-1)﹥0
∴f(m)﹥-f(2m-1)
又f(x)在(-2,2)上为奇函数
∴-f(2m-1)=f(1-2m)
∴f(m)﹥f(1-2m)
又已知f(x)是定义在(-2,2)上的减函数
 …………………………3
…………………………3
∴实数m的取值范围为(-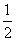 ,
, )………4
)………4
16.(14分)已知函数f(x)是定义在(-2,2)上的减函数,且为奇函数。使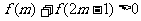 .求实数m的取值范围。
.求实数m的取值范围。
15.①
已知:f( +1)=x+2
+1)=x+2 ; 求出f(x)的解析式;
; 求出f(x)的解析式;
解:f(x)=x2-1 (x≥1) 5+2
② 已知f(x)是奇函数,g(x)是偶函数,若f(x)+g(x)=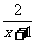 ,求f(x)和g(x).
,求f(x)和g(x).
解: …………………………..3
…………………………..3
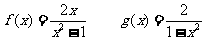 ……………………2+2
……………………2+2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com