
2. 在0.1 mol/l的NH3·H2O溶液中,下列关系正确的是
A.C(NH3·H2O)>C(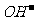 )>C(
)>C(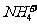 )>C(H+)
)>C(H+)
B.C(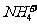 )>C(NH3·H2O)>C(
)>C(NH3·H2O)>C(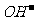 )>C(H+)
)>C(H+)
C.C(NH3·H2O)>C(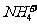 )=C(
)=C(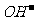 )>C(H+)
)>C(H+)
D.C(NH3·H2O)>C(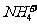 )>C(H+)>C(
)>C(H+)>C(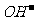 )
)
[答案]A。
[方法要领]NH3·H2O是一元弱酸,属于弱电解质,在水溶液中少部分发生电离(NH3·H2O 
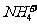 +
+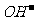 ),所以C(NH3·H2O)必大于C(NH4+)及C(
),所以C(NH3·H2O)必大于C(NH4+)及C(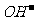 )。因为C(
)。因为C(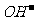 )=C(H+)+C(
)=C(H+)+C(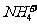 ),所以C(
),所以C(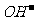 )>C(
)>C(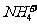 )。综合起来,C(NH3·H2O)>C(
)。综合起来,C(NH3·H2O)>C(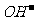 )>C(
)>C(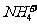 )>C(H+)21世纪教育网
)>C(H+)21世纪教育网
1. 能促进水的电离,并使溶液中C(H+)>C(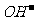 )的操作是 ( )
)的操作是 ( )
(1)将水加热煮沸 (2)向水中投入一小块金属钠 (3)向水中通CO2 (4)向水中通
NH3 (5)向水中加入明矾晶体 (6)向水中加入NaHCO3固体 (7)向水中加NaHSO4固体
A.(1)(3)(6)(7) B.(1)(3)(6) C.(5)(7) D.(5)
[答案] D
[方法要领]本题主要考查外界条件对水的电离平衡的影响,请按如下思路完成本题的解:本题涉及到哪些条件对水的电离平衡的影响?各自对水的电离平衡如何影响?结果任何(C(H+)与C(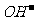 )相对大小)?归纳酸、碱、盐对水的电离平衡的影响。
)相对大小)?归纳酸、碱、盐对水的电离平衡的影响。
23.(本小题为必做题,满分10分)
在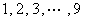 这
这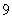 个自然数中,任取
个自然数中,任取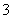 个不同的数.
个不同的数.
(1)求这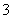 个数中至少有
个数中至少有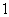 个是偶数的概率;
个是偶数的概率;
(2)求这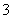 个数和为18的概率;
个数和为18的概率;
(3)设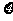 为这
为这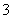 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为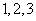 ,则有两组相邻的数
,则有两组相邻的数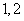 和
和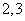 ,此时
,此时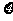 的值是
的值是 ).求随机变量
).求随机变量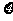 的分布列及其数学期望
的分布列及其数学期望 .
.
江苏省诚贤中学10-11学年高三上学期10月月考
22.(本小题为必做题,满分10分)
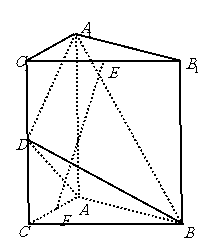 如图,直三棱柱
如图,直三棱柱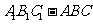 中,
中, 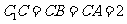 ,
,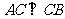 .
. 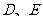 分别为棱
分别为棱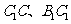 的中点.
的中点.
(1)求点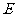 到平面
到平面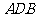 的距离;
的距离;
(2)求二面角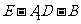 的平面角的余弦值;
的平面角的余弦值;
(3)在线段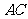 上是否存在一点
上是否存在一点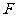 ,使得
,使得
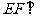 平面
平面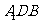 ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
20.(本小题满分16分)
已知函数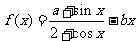
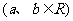 ,
,
(Ⅰ)若 在
在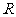 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为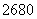 ,试求
,试求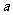 和
和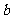 的值。
的值。
(Ⅱ)若 为奇函数,
为奇函数,
(1)是否存在实数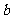 ,使得
,使得 在
在 为增函数,
为增函数,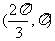 为减函数,若存在,求出
为减函数,若存在,求出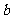 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当 时,都有
时,都有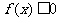 恒成立,试求
恒成立,试求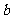 的取值范围。
的取值范围。
B.附加题部分
(本大题共6小题,其中第21-24题为选做题,请考生在第21题中任选2个小题作答,如果多做,则按所选做的前两题记分;第25和第26题为必做题.解答应写出文字说明,证明过程或演算步骤.)
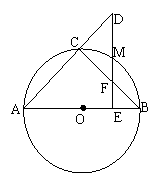 A.(本小题为选做题,满分10分)
A.(本小题为选做题,满分10分)
如图,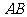 是
是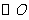 的直径,
的直径,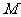 为圆上一点,
为圆上一点,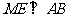 ,垂足为
,垂足为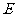 ,点
,点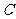 为
为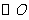 上任一点,
上任一点,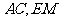 交于点
交于点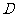 ,
, 交
交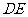 于点
于点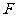 .
.
求证:(1)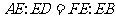 ;(2)
;(2)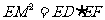 .
.
B.(本小题为选做题,满分10分)
设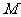 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到 倍,纵坐标伸长到
倍,纵坐标伸长到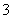 倍的伸压变换.
倍的伸压变换.
(1)求矩阵 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(2)求逆矩阵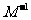 以及椭圆
以及椭圆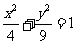 在
在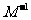 的作用下的新曲线的方程.
的作用下的新曲线的方程.
C.(本小题为选做题,满分10分)
已知点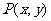 是圆
是圆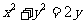 上的动点.
上的动点.
(1)求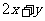 的取值范围;
的取值范围;
(2)若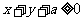 恒成立,求实数
恒成立,求实数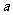 的取值范围.
的取值范围.
D.(本小题为选做题,满分10分)
已知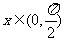 ,求函数
,求函数 的最小值以及取最小值时所对应的
的最小值以及取最小值时所对应的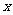 值.
值.
19.(本小题满分16分)
已知数列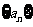 中,
中,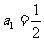 ,点
,点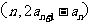 在直线
在直线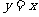 上,其中
上,其中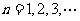 ,
,
(1)令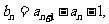 求证:数列
求证:数列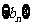 为等比数列;
为等比数列;
(2)求数列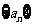 的通项;
的通项;
(3)设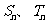 分别为数列
分别为数列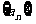
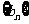 的前
的前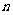 项和,是否存在实数
项和,是否存在实数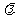 ,使得数列
,使得数列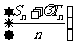 为等差数列?若存在,试求出
为等差数列?若存在,试求出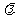 .若不存在,则说明理由.
.若不存在,则说明理由.
18.(本小题满分16分)
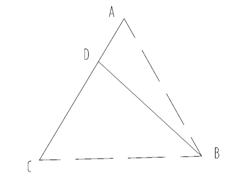 某企业有两个生产车间分别在
某企业有两个生产车间分别在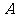 、
、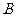 两个位置,
两个位置,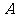 车间有100名员工,
车间有100名员工,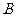 车间有400名员工,现要在公路
车间有400名员工,现要在公路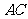 上找一点
上找一点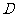 ,修一条公路
,修一条公路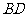 ,并在
,并在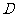 处建一个食堂,使得所有员工均在此食堂用餐,已知
处建一个食堂,使得所有员工均在此食堂用餐,已知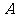 、
、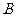 、
、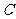 中任意两点间的距离均是1
中任意两点间的距离均是1 ,设
,设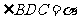 ,所有员工从车间到食堂步行的总路程为
,所有员工从车间到食堂步行的总路程为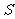 .
.
(1)写出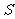 关于
关于 的函数表达式,并指出
的函数表达式,并指出 的取值范围;
的取值范围;
(2)问食堂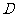 建在距离
建在距离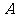 多远时,可使总路程
多远时,可使总路程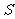 最少?
最少?
17、(本小题满分14分)
已知椭圆C的左、右焦点坐标分别是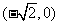 ,
,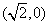 ,离心率是
,离心率是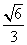 ,直线y=t椭圆C交与不同的两点M,N,以线段为直径作圆P,圆心为P。
,直线y=t椭圆C交与不同的两点M,N,以线段为直径作圆P,圆心为P。
(1)求椭圆C的方程;
(2)若圆P与x轴相切,求圆心P的坐标;
(3)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值。
16.(本小题满分14分)
 在平行四边形
在平行四边形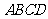 中,设
中,设 ,
,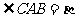 ,已知
,已知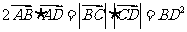 ,
, 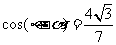 ,其中
,其中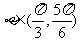 ;
;
(1)求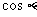 的值;(2)求
的值;(2)求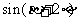 的值。
的值。
15.(本小题满分14分)
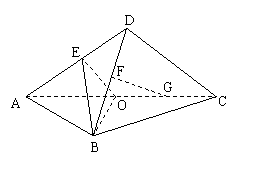 如图,
如图,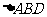 和
和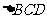 都是等边三角形,
都是等边三角形,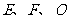 分别是
分别是 的中点,
的中点,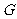 是
是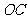 的中点;
的中点;
(1)求证: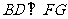 ;(2)求证:
;(2)求证: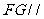 平面
平面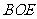 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com