22．(本小题满分14分)

设函数f(x)是定义在［-1，0)∪(0，1］上的奇函数，当x∈［-1，0)时，f(x)=2ax+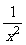 (a∈R)．

　　　 (1)求函数f(x)的解析式；

　　　 (2)若a＞-1，试判断f(x)在(0，1］上的单调性；

　　　 (3)是否存在实数a，使得当x∈(0,1］时，f(x)有最大值-6．

21．(本小题满分12分)

某企业拟在2011年度进行一系列促销活动，已知其产品年销量x万件与年促销费用t万元之间满足3-x与t+1成反比例，当年促销费用t=0万元时，年销量是1万件．已知2011年产品的设备折旧、维修等固定费用为3万元，每生产1万件产品需再投入32万元的生产费用，若将每件产品售价定为：其生产成本的150%与“平均每件促销费的一半”之和，则当年生产的商品正好能销完．

　　　 (1)将2011年的利润y(万元)表示为促销费t(万元)的函数；

　　　 (2)该企业2011年的促销费投入多少万元时，企业年利润最大？

　　　 (注：利润=销售收入-生产成本-促销费，生产成本=固定费用+生产费用)

20．(本小题满分12分)

已知定义在R上的函数f(x)=x²(ax-3)，其中a为常数．

　　　 (Ⅰ)若x=1是函数f(x)的一个极值点，求a的值；

　　　 (Ⅱ)若函数f(x)在区间(-1，0)上是增函数，求a的取值范围．

19．(本小题满分12分)

已知函数f(x)=cos²棕 x+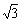 sin棕xcos棕x+k(其中0＜棕＜仔，k∈R)当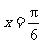时取得最大值3．

　　　 (Ⅰ)求函数f(x)的周期和单调减区间；

　　　 (Ⅱ)求函数f(x)在(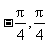)上的最大值和最小值．

18．(本小题满分12分)

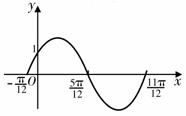
函数f₁(x)=Asin(棕 x+渍)(A＞0，棕＞0，｜渍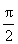｜＜)的一段图象过点(0，1)，如图所示．

(1)求函数f₁(x)的表达式；

　　　 (2)将函数y=f₁(x)的图象向右平移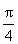个单位，得函数y=f₂(x)的图象，求y=f₂(x)的最大值，并求出此时自变量x的集合．

17．(本小题满分12分)

已知集合A={x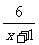｜≥1，x∈R}，B= {x｜x²-2x-m＜0}．

　　　 (Ⅰ)当m=3时，求A∩(C_RB)；

　　　 (Ⅱ)若A∩B={x｜-1＜x＜4}，求实数m的值．

16．给出下列四个结论：

　　　 ①函数y=a^x(a＞0且a≠1)与函数y=log_aa^x(a＞0且a≠1)的定义域相同；

　　　 ②函数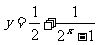(x≠0)是奇函数；

　　　 ③函数y = sin(-x)在区间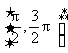上是减函数；

　　　 ④函数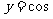｜x｜是周期函数．

　　　 其中正确结论的序号是　　　 　　　　．(填写你认为正确的所有结论序号)

15．设f(x)是定义在R上的以3为周期的奇函数，若f(1)＞1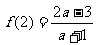，，则a的取值范围是　　　 ．

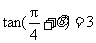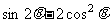14．已知，则的值为　　　　 ．

13．由直线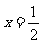，x=2，曲线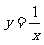及x轴所围成的曲边梯形的面积为　　　　 ．