
6.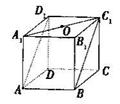 如右图,正方体
如右图,正方体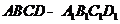 的棱长为
的棱长为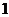 ,点
,点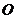 是底面
是底面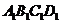 的中心,则点
的中心,则点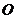 到平面
到平面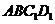 的距离为 (
)
的距离为 (
)
A.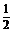 B.
B.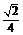 C.
C. D.
D.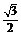
5.若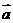 是非零向量,则命题“
是非零向量,则命题“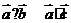 ”是命题“
”是命题“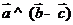 ”成立的
( )
”成立的
( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
4. 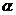 、
、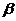 、
、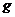 表示平面,
表示平面,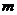 、
、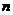 、
、 表示直线,如下四个命题,其中使“
表示直线,如下四个命题,其中使“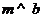 ”成立的一个充分条件
( )
”成立的一个充分条件
( )
A. 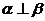 ,
,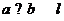 ,
,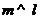 B.
B. 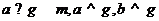
C.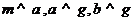 D.
D.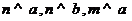
3.如果直线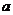 ∥平面
∥平面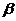 ,那么下列命题正确的是
( )
,那么下列命题正确的是
( )
A.平面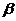 内有且只有一条直线与
内有且只有一条直线与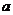 平行 B.平面
平行 B.平面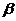 内有且只有一条直线与
内有且只有一条直线与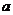 垂直
垂直
C.平面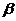 内有无数条直线与
内有无数条直线与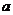 不平行
D.平面
不平行
D.平面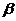 内不存在与
内不存在与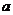 垂直的直线
垂直的直线
2.直线 与平面
与平面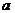 所成的角为
所成的角为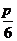 ,则直线
,则直线 与平面
与平面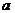 内的所有直线所成角中最大、最小的分别是( )
内的所有直线所成角中最大、最小的分别是( )
A. 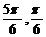 B.
B.
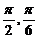 C.
C.
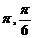 D.
D.
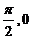
1.对于任意的直线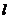 与平面
与平面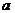 ,在平面
,在平面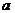 内必有直线
内必有直线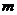 ,使得直线
,使得直线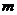 与直线
与直线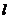 的关系是 (
)
的关系是 (
)
A. 平行 B.相交 C. 垂直 D. 互为异面直线
21.(本题满分14分)
某种产品每件成本为6元,每件售价为x元(x>6),年销量为u万件,若已知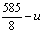 与
与
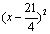 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润y关于x的函数关系式;
(2)求售价为多少时,年利润最大,并求出最大年利润.
20.(本题满分14分)
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,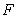 为
为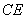 上的点,
上的点,
且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)求三棱锥D-AEC的体积;
(3)设M在线段AB上,且满足AM=2MB,
试在线段CE上确定一点N,使得MN∥平面DAE.
19.(本小题满分12分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5
人,现从中选2人.设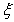 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且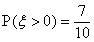 .
.
 (I) 求文娱队的人数; (II) 写出
(I) 求文娱队的人数; (II) 写出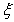 的概率分布列并计算
的概率分布列并计算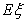 .
.
18.(本题满分14分) 已知A(0,-1) ,B(0,1)
直线AM,BM相交于点M,且它们的斜率之积为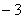 ,
,
(1)求动点M的轨迹方程
(2)设过点(0,-2)的直线L与动点M的轨迹交于C、D两点,且
求直线L的方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com