
2.已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
|
|
甲 |
乙 |
丙 |
|
维生素A(单位/千克) |
600 |
700 |
400 |
|
维生素B(单位/千克) |
800 |
400 |
500 |
|
成本(元/千克) |
11 |
9 |
4 |
(Ⅰ)用x,y表示混合食物成本c元; (Ⅱ)确定x,y,z的值,使成本最低.
解:(Ⅰ)由题,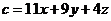 ,又
,又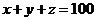 ,所以,
,所以, .
.
(Ⅱ)由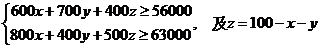 得,
得, ,
,
所以,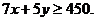 所以,
所以,

当且仅当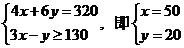 时等号成立.
时等号成立.
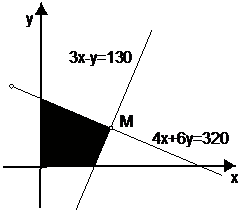 所以,当x=50千克,y=20千克,z=30千克时,混合物成本最低,为850元.
所以,当x=50千克,y=20千克,z=30千克时,混合物成本最低,为850元.
点评:本题为线性规划问题,用解析几何的观点看,问题的解实际上是由四条直线所围成的区域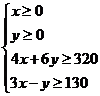 上使得
上使得 最大的点.不难发现,应在点M(50,20)处取得.
最大的点.不难发现,应在点M(50,20)处取得.
[名师点睛]①求线性目标函数在约束条件下的最值问题,统称为线性规划问题;
②可行解:指满足线性约束条件的解(x,y);
可行域:指由所有可行解组成的集合;
[试题演练]
1.预算用2000元购买单件为50元的桌子和20元的椅子,希望使桌椅的总数尽可能的多,但椅子不少于桌子数,且不多于桌子数的1.5倍,问桌、椅各买多少才行?
解:设桌椅分别买x,y张,把所给的条件表示成不等式组,即约束条件
为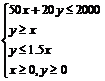 由
由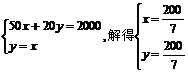 ∴A点的坐标为(
∴A点的坐标为(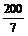 ,
,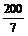 )由
)由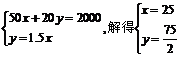 ∴B点的坐标为(25,
∴B点的坐标为(25,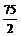 )
)
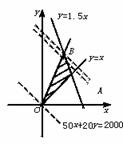 所以满足约束条件的可行域是以A(
所以满足约束条件的可行域是以A(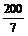 ,
,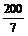 ),B(25,
),B(25,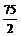 ),O(0,0)为顶点的三角形区域(如右图)由图形直观可知,目标函数z=x+y在可行域内的最优解为(25,
),O(0,0)为顶点的三角形区域(如右图)由图形直观可知,目标函数z=x+y在可行域内的最优解为(25, ),但注意到x∈N,y∈N*,故取y=37.故有买桌子25张,椅子37张是最好选择.
),但注意到x∈N,y∈N*,故取y=37.故有买桌子25张,椅子37张是最好选择.
2.已知直线l过点P(3,1)且被两平行线l1:x+y+1=0,l2:x+y+6=0截得的线段长为5,求直线l的方程.
解 方法一 若直线l的斜率不存在,则直线l的方程为x=3,此时与l1,l2的交点分别是
A(3,-4),B(3,-9),截得的线段长|AB|=|-4+9|=5,符合题意.
若直线l的斜率存在时,则设直线l的方程为y=k(x-3)+1,分别与直线l1,l2的方程联立,
由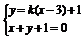 ,解得A
,解得A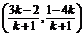 . 由
. 由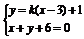 ,解得B
,解得B ,
, 
由两点间的距离公式,得 +
+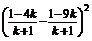 =25,
=25,
1.求过两直线l1:x+y+1=0,l2:5x-y-1=0的交点,且与直线3x+2y+1=0的夹角为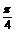 的直线方程.
的直线方程. 
解 设所求直线方程为x+y+1+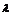 (5x-y-1)=0, 即(1+5
(5x-y-1)=0, 即(1+5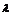 )x+(1-
)x+(1-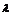 )y+1-
)y+1-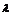 =0.
=0. 
因为所求直线与直线3x+2y+1=0的夹角为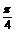 , 所以tan
, 所以tan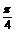 =
=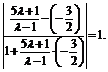

解得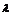 =-
=-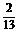 . ∴所求直线方程为x+5y+5=0.
. ∴所求直线方程为x+5y+5=0. 
又直线l2:5x-y-1=0与直线3x+2y+1=0的夹角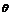 满足tan
满足tan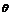 =
=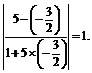

∴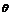 =
=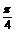 ,故直线l2也是符合条件的一解. 综上所述,所求直线方程为 x+5y+5=0或5x-y-1=0.
,故直线l2也是符合条件的一解. 综上所述,所求直线方程为 x+5y+5=0或5x-y-1=0. 
[名师点睛]
1.直线l1与直线l2的的平行与垂直

(1)若l1,l2均存在斜率且不重合:①l1//l2 k1=k2;②l1
k1=k2;②l1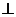 l2
l2 k1k2=-1。
k1k2=-1。

(2)若


若A1、A2、B1、B2都不为零。①l1//l2
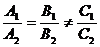 ;②l1
;②l1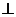 l2
l2 A1A2+B1B2=0;③l1与l2相交
A1A2+B1B2=0;③l1与l2相交
 ;④l1与l2重合
;④l1与l2重合
 ;
;
注意:若A2或B2中含有字母,应注意讨论字母=0与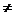 0的情况。两条直线的交点:两条直线的交点的
0的情况。两条直线的交点:两条直线的交点的 则:
则: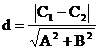 。注意点:x,y对应项系数应相等.
。注意点:x,y对应项系数应相等.

(3)点到直线的距离: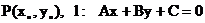 ,则P到l的距离为:
,则P到l的距离为: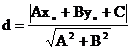


[试题演练]
4]《中学化学教学参考》2007年,陕西师范大学杂志社。
3] 韩立福著:《新课程教师科研行动指要》,首都师范大学出版社,2006年版。
2]《化学课程标准》(实验稿),北京师范大学出版社,2001年7月第1版。
1]韩立福著:《新课程有效课堂教学行动策略》,首都师范大学出版社,2006年版。
6、某硝酸铵样品经测定含氮38%,则该样品中可能含有的一种化肥为( )
A.(NH4)2SO4 B.NH4HCO3 C.NH4Cl H2)2
反思与总结:

 NH4NO3~2N
NH4NO3~2N
物质的质量=某元素的质量/某元素的质量分数 80 28
 某元素的质量=某物质的质量×某元素的质量分数 X Y
某元素的质量=某物质的质量×某元素的质量分数 X Y
组合计算:大的小的组合成中间 大值>中间值>小值 a% b%

评价:
参考文献:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com