
3.区分分运动和合运动的基本方法是:合运动是物体的实际运动轨迹。
 题型2. (平抛(或类平抛)运动问题)如图所示,AB为竖直墙壁,A点和P点在同一水平面上。空间存 在着竖直方向的匀强电场。将一带电小球从P点以速度
题型2. (平抛(或类平抛)运动问题)如图所示,AB为竖直墙壁,A点和P点在同一水平面上。空间存 在着竖直方向的匀强电场。将一带电小球从P点以速度 向A抛出,结果打在墙上的C处。若撤去电场,将小球从P点以初速
向A抛出,结果打在墙上的C处。若撤去电场,将小球从P点以初速 向A抛出,也正好打在墙上的C点。求:
向A抛出,也正好打在墙上的C点。求:
(1)第一次抛出后小球所受电场力和重力之比
(2)小球两次到达C点时速度之比
解析:(1)设AC=h、电场力为FQ,根据牛顿第二定律得:FQ+mg=ma①
第一次抛出时,h=  ② (1分 )
② (1分 )
第二次抛出时,h= ③ (1分 )
③ (1分 )
由②、③两式得a=4g ④ (1分 )
所以,FQ:G=3:1 ⑤ (1分 )
(2)第一次抛出打在C点的竖直分速度 y1=a(
y1=a( )⑥ (1分 )
)⑥ (1分 )
第二次抛出打在C点的竖直分速度 y2=g(
y2=g( )⑦ (1分 )
)⑦ (1分 )
第一次抛出打在C点的速度 1=
1= ⑧ (1分 )
⑧ (1分 )
第二次抛出打在C点的速度 2=
2= ⑨ (1分 )
⑨ (1分 )
所以, 1:
1: 2=2:1⑩ (1分 )
2=2:1⑩ (1分 )
规律总结:平抛(或类平抛)运动处理的基本方法就是把运动分解为水平方向的匀速运动和竖直方向的匀加速运动。通过研究分运动达到研究合运动的目的。
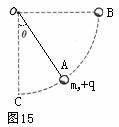 题型3.(竖直平面内的圆周运动问题)如图15所示,质量为 m、电量为+q的带电小球固定于一不可伸长的绝缘细线一端,绳的另一端固定于O点,绳长为
题型3.(竖直平面内的圆周运动问题)如图15所示,质量为 m、电量为+q的带电小球固定于一不可伸长的绝缘细线一端,绳的另一端固定于O点,绳长为 ,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平和右的匀强电场,小球静止于与竖直方向成 θ=300角的A点。求:
,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平和右的匀强电场,小球静止于与竖直方向成 θ=300角的A点。求:
(1)小球静止在A点处绳子受到的拉力;
(2) 外加电场大小;
(3)将小球拉起至与O点等高的B点后无初速释放,则小球经过最低点C时,绳受到的拉力。
解析:(1)带电粒子A处于平衡,其受力如图,其中F为两点电荷间的库仑力,T为绳子拉力 ,E0为外加电场,则
,E0为外加电场,则
Tcosθ-mg-Fcosθs=0 1 (2分)
Fsinθ+qE0-Tsinθ=0 2 (2分)
 3 (2分)
3 (2分)
联立式解得:有
 4 (2分)
4 (2分)
 5 (2分)
5 (2分)
(2)小球从B运动到C的过程中,q与Q间的库仑力不做功,由动能定理得
 6 (2分)
6 (2分)
在C点时:
 7 (2分)
7 (2分)
联立5、6、7解得:
 8 (2分)
8 (2分)
审题指导:1.要注意对小球受力分析,不要漏掉库仑力。
题型1.(运动的合成与分解问题)若河水的流速大小与水到河岸的距离有关,河中心水的流速最大,河岸边缘处水的流速最小 现假设河的宽度为120m,河中心水的流速大小为4m/s,船在静水中的速度大小为3m/s,要使般以最短时间渡河,则 ( )
现假设河的宽度为120m,河中心水的流速大小为4m/s,船在静水中的速度大小为3m/s,要使般以最短时间渡河,则 ( )
A.船渡河的最短时间是24s
B.在行驶过程中,船头始终与河岸垂直
C.船在河水中航行的轨迹是一条直线
D.般在河水中的最大速度为5m/s
解析:根据分运动具有独立性和等时性可知,当船头与河岸垂直过河时,时间t最短,t=120/3=40s,A错,B对;船速是恒定的,但是水流速度与水到河岸的距离有关,合速度的大小和方向都在不断变化,轨迹为曲线,C错;船在河水中的速度是指合运动的速度  最大,D正确。
最大,D正确。
规律总结:1.合运动与分运动具有等时性,分运动具有独立性,这一原理经常应用解决小船过河即平抛运动问题。
2.运动的合成与分解的依据仍然是平行四边形定则。
此专题复习时,可以先让学生完成相应的习题,在精心批阅之后以题目带动知识点,进行适当提炼讲解。根据我对学生的了解,发现很多同学对这个专题中的:
① 几个物理模型构建不理想,如平抛运动、类平抛运动、匀速圆周运动、天体运动等同于匀速圆周运动
② 模型建立好了,但是处理问题时方法选择不恰当
所以在讲解时层次应放的低一点,着重掌握好各种物理模型,理解处理各种模型的方法,坚持夯实基础为主的主线。
|
考点 |
要求 |
考点解读 |
|
运动的合成与分解 |
Ⅱ |
本专题的重点是运动的合成与分解、平抛运动和圆周运动。特点是综合性请、覆盖面广、纵横联系点多。可以有抛体运动与圆周运动或直线运动间多样组合,还可以与电场、磁场知识综合,命题的思路依然是以运动为线索进而从力、能量角度进行考查。应用万有引力定律解决天体运动、人造地球卫星运动、变轨问题。应该从以下几个方面进行重视:①直线运动、平抛运动和圆周运动的组合性问题,主要考查运动的合成与分解、动力学特征和功能关系②应用分解与合成的思想解决带电粒子在各种场中的类平抛运动问题;应用圆周运动的知识解决混合场内的圆周运动问题 ③以我国飞速发展的航天事业为背景,凸显最新科技动态,应用万有引力定律解决卫星发射和回收变转过程中各物理量的比较和功能转化。 ③以我国飞速发展的航天事业为背景,凸显最新科技动态,应用万有引力定律解决卫星发射和回收变转过程中各物理量的比较和功能转化。 |
|
抛体运动 |
Ⅱ |
|
|
匀速圆周运动、角速度、线速度、向心加速度 |
Ⅰ |
|
|
匀速圆周运动的向心力 |
Ⅱ |
|
|
离心现象 |
Ⅰ |
|
|
万有引力定律及应用 |
Ⅱ |
|
|
环绕速度 |
Ⅱ |
|
|
第二宇宙速度和第三宇宙速度 |
Ⅰ |
4.天体质量M、密度 的估算
的估算
(1)从环绕天体出发:通过观测环绕天体运动的周期T和轨道半径r;就可以求出中心天体的质量M
(2)从中心天体本身出发:只要知道中心天体的表面重力加速度g和半径R就可以求出中心天体的质量M。
3. 三种宇宙速度:第一、第二、第三宇宙速度
⑴第一宇宙速度(环绕速度):是卫星环绕地球表面运行的速度,也是绕地球做匀速圆周运动的最大速度,也是发射卫星的最小速度V1=7.9Km/s。
⑵第二宇宙速度(脱离速度):使物体挣脱地球引力束缚的最小发射速度,V2=11.2Km/s。
⑶第三宇宙速度(逃逸速度):使物体挣脱太阳引力束缚的最小发射速度,V3=16.7 Km/s。
2.卫星的绕行速度、角速度、周期、频率和半径r的关系:
⑴由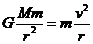 ,得
,得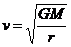 ,所以r越大,v越小。
,所以r越大,v越小。
⑵由 ,得
,得 ,所以r越大,
,所以r越大, 越小
越小
⑶由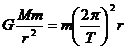 ,得
,得 ,所以r越大,T越大。
,所以r越大,T越大。
⑷由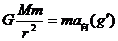 ,得
,得 ,所以r越大,a向(g/)越小。
,所以r越大,a向(g/)越小。
1.在处理天体的运动问题时,通常把天体的运动看成是匀速圆周运动,其所需要的向心力由万有引力提供,其基本关系式为: ,
,
在天体表面,忽略星球自转的情况下:
5.平抛(类平抛)运动是匀变速曲线运动,物体所受的合外力为恒力,而圆周运动是变速运动,物体所受的合外力为变力,最起码合外力的方向时刻在发生变化。
4.描述圆周运动的几个物理量为:角速度 ,线速度v,向心加速度a,周期T,频率f。其关系为:
,线速度v,向心加速度a,周期T,频率f。其关系为:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com