
1.(2009年广东卷文)已知平面向量a=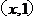 ,b=
,b=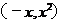 , 则向量
, 则向量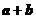

A平行于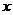 轴
B.平行于第一、三象限的角平分线
轴
B.平行于第一、三象限的角平分线 
C.平行于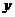 轴 D.平行于第二、四象限的角平分线
轴 D.平行于第二、四象限的角平分线 
[答案]
[解析]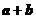
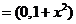 ,由
,由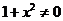 及向量的性质可知,C正确.
及向量的性质可知,C正确.
[名师点睛]向量的坐标表示实际上就是向量的代数表示.在引入向量的坐标表示后,使向量之间的运算代数化,这样就可以将“形”和“数”紧密地结合在一起.因此,许多平面几何问题中较难解决的问题,都可以转化为大家熟悉的代数运算的论证.也就是把平面几何图形放到适当的坐标系中,赋予几何图形有关点与平面向量具体的坐标,这样将有关平面几何问题转化为相应的代数运算和向量运算,从而使问题得到解决.
 [试题演练]
[试题演练]
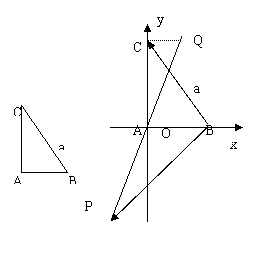
如图在Rt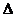 ABC中,已知BC=a,若长为2a的线段PQ以A为中点,问
ABC中,已知BC=a,若长为2a的线段PQ以A为中点,问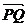 与
与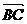 的夹角
的夹角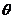 取何值时,
取何值时, 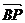
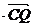 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。





解:以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角坐标系。设|AB|=c,|AC|=b,则A(0,0),B(c,0),C(0,b).且|PQ|=2a,|BC|=a.设点P的坐标为(x,y),则Q(-x,-y),

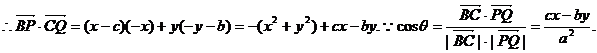

∴cx-by=a2cos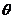 .∴
.∴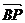
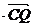 =- a2+ a2cos
=- a2+ a2cos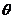 .故当cos
.故当cos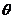 =1,即
=1,即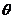 =0(
=0(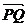
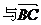 方向相同)时,
方向相同)时,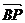
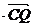 的值最大,其最大值为0.
的值最大,其最大值为0.
点评:本题主要考查向量的概念,运算法则及函数的有关知识,平面向量与几何问题的融合。考查学生运用向量知识解决综合问题的能力。

[三年高考]
07、08、09 高考试题及其解析
2009高考试题及解析
[名师点睛]平面向量与函数交汇的问题,主要是向量与二次函数结合的问题为主,要注意自变量的取值范围。
[试题演练]已知向量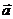 =(cos
=(cos x,sin
x,sin x),
x),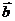 =(
=(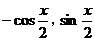 ),且x∈[0,
),且x∈[0,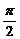 ].
].
(1)求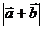 (2)设函数
(2)设函数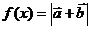 +
+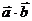 ,求函数
,求函数 的最值及相应的
的最值及相应的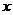 的值。
的值。
解:(错误!未找到引用源。)由已知条件: 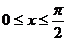 , 得:
, 得:
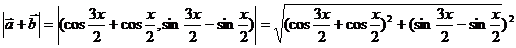

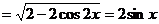

(2)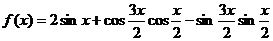
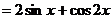

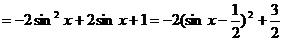 因为:
因为: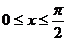 ,所以:
,所以: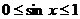

所以,只有当: 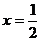 时,
时, 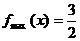
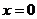 ,或
,或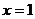 时,
时,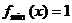

点评:本题考查向量、三角函数、二次函数的知识,经过配方后,变成开口向下的二次函数图象,要注意sinx的取值范围,否则容易搞错。
3、将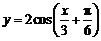 的图象按向量
的图象按向量 平移,则平移后所得图象的解析式为( )
平移,则平移后所得图象的解析式为( )
A.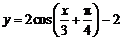 B.
B.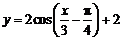

C.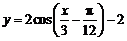 D.
D.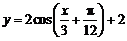

解: 由向量平移的定义,在平移前、后的图像上任意取一对对应点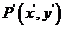 ,
,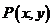 ,则
,则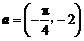
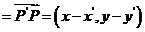
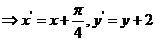 ,代入到已知解析式中可得选A
,代入到已知解析式中可得选A
点评:本题主要考察向量与三角函数图像的平移的基本知识,以平移公式切入,为中档题。注意不要将向量与对应点的顺序搞反,或死记硬背以为是先向右平移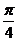 个单位,再向下平移2个单位,误选C
个单位,再向下平移2个单位,误选C
2、 在
在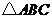 中,角
中,角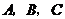 的对边分别为
的对边分别为 .
.
(1)求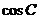 ;
;
(2)若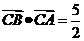 ,且
,且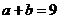 ,求
,求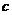 .
.
解:(1)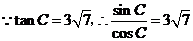

又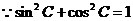 解得
解得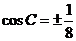 .
.
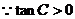 ,
,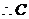 是锐角.
是锐角. 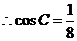 .
.
(2)由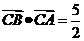 ,
, 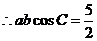 ,
, 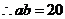 .
.
又
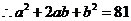 .
. 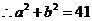 .
.
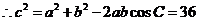 .
. 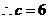 .
.
点评:本题向量与解三角形的内容相结合,考查向量的数量积,余弦定理等内容。
[名师点睛]向量与三角函数的综合问题是高考经常出现的问题,考查了向量的知识,三角函数的知识,达到了高考中试题的覆盖面的要求。
[试题演练]
1、已知向量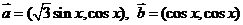 ,函数
,函数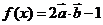

(1)求 的最小正周期; (2)当
的最小正周期; (2)当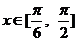 时, 若
时, 若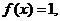 求
求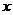 的值.
的值.
解:(1)
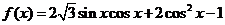
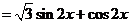
 .
. 
所以,T=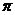 .
. 
(2) 由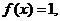 得
得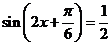 ,
,
∵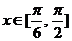 ,∴
,∴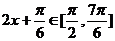 ∴
∴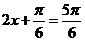 ∴
∴ 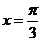

4、在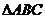 中,
中,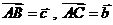 ,若点
,若点 满足
满足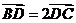 ,则
,则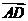 =(
).
=(
).

A. 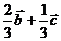 B.
B. 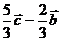 C.
C. 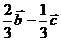 D.
D. 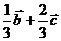

[解法一]∵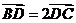 ∴
∴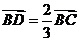

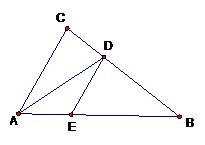 ∴
∴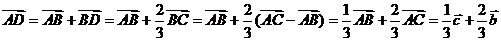 .
.
 [试题演练]
[试题演练]
设D、E、F分别是△ABC的三边BC、CA、AB上的点,且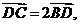
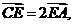
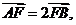 则
则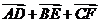 与
与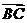 ( )
( )
A.反向平行 B.同向平行 C.互相垂直 D.既不平行也不垂直 
解:由定比分点的向量式得: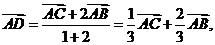 同理,有:
同理,有: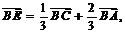
 以上三式相加得
以上三式相加得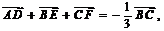 所以选A.
所以选A.
点评:利用定比分点的向量式,及向量的运算,是解决本题的要点.
3、已知平面向量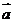 =(1,-3),
=(1,-3),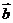 =(4,-2),
=(4,-2),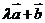 与
与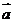 垂直,则
垂直,则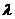 是( )
是( )
A. -1 B. 1 C.
-2 D.
2
解:由于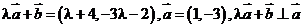

∴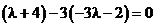 ,即
,即 ,选A
,选A
点评:本题考查简单的向量运算及向量垂直的坐标运算,注意不要出现运算出错,因为这是一道基础题,要争取满分。
2、已知平面向量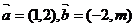 ,且
,且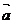 ∥
∥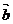 ,则
,则 =( )
=( )
A.(-2,-4) B. (-3,-6) C. (-4,-8) D. (-5,-10)
解:由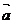 ∥
∥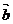 ,得m=-4,所以,
,得m=-4,所以,
 =(2,4)+(-6,-12)=(-4,-8),故选(C)。
=(2,4)+(-6,-12)=(-4,-8),故选(C)。
点评:两个向量平行,其实是一个向量是另一个向量的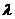 倍,也是共线向量,注意运算的公式,容易与向量垂直的坐标运算混淆。
倍,也是共线向量,注意运算的公式,容易与向量垂直的坐标运算混淆。
[名师点睛]向量的运算要求掌握向量的加减法运算,会用平行四边形法则、三角形法则进行向量的

[试题演练]
1、设a=(1,-2),b=(-3,4),c=(3,2),则(a+2b)·c=( )
A.(-15,12) B.0
C.-3 D.-11
解:(a+2b) ,(a+2b)·c
,(a+2b)·c 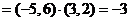 ,选C
,选C
点评:本题考查向量与实数的积,注意积的结果还是一个向量,向量的加法运算,结果也是一个向量,还考查了向量的数量积,结果是一个数字。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com