
1(北京4)已知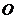 是
是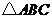 所在平面内一点,
所在平面内一点, 为
为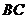 边中点,且
边中点,且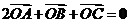 ,那么( A )
,那么( A )
A.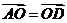 B.
B.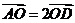 C.
C.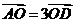 D.
D.
2(辽宁3)若向量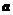 与
与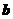 不共线,
不共线,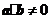 ,且
,且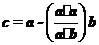 ,则向量
,则向量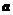 与
与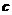 的夹角为( D )
的夹角为( D )
A.0 B.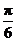 C.
C.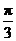 D.
D.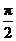
3(辽宁6)若函数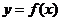 的图象按向量
的图象按向量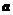 平移后,得到函数
平移后,得到函数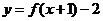 的图象,则向量
的图象,则向量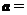 ( A )
( A )
A. B.
B.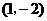 C.
C.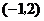 D.
D.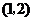
4(宁夏,海南4)已知平面向量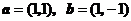 ,则向量
,则向量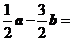 ( D )
( D )
A.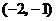 B.
B.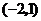 C.
C. D.
D.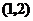
5.(福建4)对于向量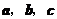 和实数
和实数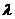 ,下列命题中真命题是( B )
,下列命题中真命题是( B )
A.若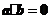 ,则
,则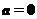 或
或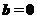 B.若
B.若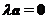 ,则
,则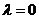 或
或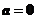
C.若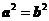 ,则
,则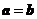 或
或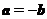 D.若
D.若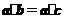 ,则
,则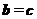
6(湖北2)将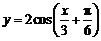 的图象按向量
的图象按向量 平移,则平移后所得图象的解析式为( A )
平移,则平移后所得图象的解析式为( A )
A.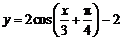 B.
B.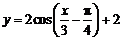 C.
C.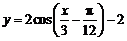 D.
D.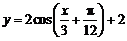
7(湖北文9)设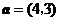 ,
,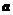 在
在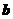 上的投影为
上的投影为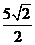 ,
,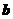 在
在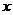 轴上的投影为2,且
轴上的投影为2,且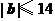 ,则
,则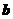 为( B )
为( B )
A.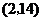 B.
B.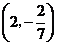 C.
C.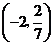 D.
D.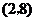
8(湖南4)设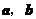 是非零向量,若函数
是非零向量,若函数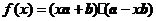 的图象是一条直线,则必有( A )
的图象是一条直线,则必有( A )
A. B.
B.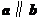 C.
C.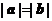 D.
D.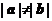
9(湖南文2)若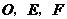 是不共线的任意三点,则以下各式中成立的是( B
)
是不共线的任意三点,则以下各式中成立的是( B
)
A.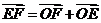 B.
B.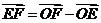
C.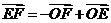 D.
D.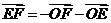
10(四川7)设A{a,1},B{2,b},C{4,5},为坐标平面上三点,O为坐标原点,若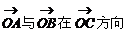 上的投影相同,则a与b满足的关系式为 ( A )
上的投影相同,则a与b满足的关系式为 ( A )
(A)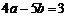 (B)
(B)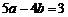 (C)
(C) (D)
(D)
11(天津10)设两个向量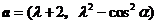 和
和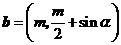 ,其中
,其中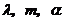 为实数.若
为实数.若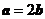 ,则
,则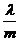 的取值范围是( A )
的取值范围是( A )
A.[-6,1] B. C.(-6,1] D.[-1,6]
C.(-6,1] D.[-1,6]
12(浙江7)若非零向量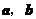 满足
满足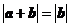 ,则( C )
,则( C )
A.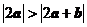 B.
B.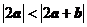 C.
C.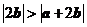 D.
D. 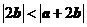
13(浙江文9)若非零向量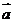 、
、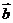 满足|
满足|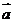 一
一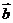 |=|
|=|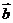 |,则(A)
|,则(A)
(A) |2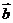 |>|
|>|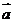 一2
一2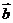 | (B) |2
| (B) |2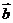 |<|
|<|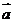 一2
一2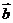 |
|
(C) |2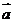 |>|2
|>|2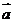 一
一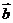 | (D) |2
| (D) |2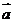 |<|2
|<|2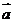 一
一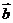 |
|
14(山东11)在直角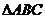 中,
中,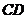 是斜边
是斜边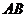 上的高,则下列等式不成立的是( C )
上的高,则下列等式不成立的是( C )
(A)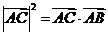 (B)
(B) 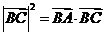
(C)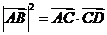 (D)
(D) 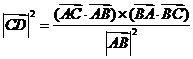
15(山东文5)已知向量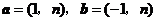 ,若
,若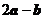 与
与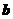 垂直,则
垂直,则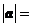 ( C )
( C )
A. B.
B.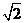 C.
C.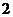 D.4
D.4
16(重庆5)在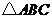 中,
中,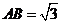 ,
,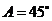 ,
,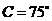 ,则
,则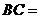 ( A )
( A )
 A.
A.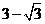 B.
B.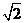 C.
C.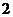 D.
D.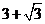
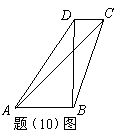
17(重庆10)如题(10)图,在四边形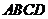 中,
中,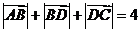 ,
,
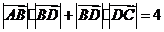 ,
,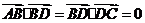 ,
,
则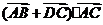 的值为( C )
的值为( C )
A.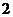 B.
B.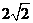 C.
C.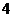 D.
D.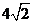
18(上海14)直角坐标系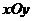 中,
中,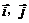 分别是与
分别是与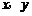 轴正方向同向的单位向量.在直角三角形
轴正方向同向的单位向量.在直角三角形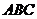 中,若
中,若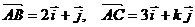 ,则
,则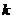 的可能值个数是( B )
的可能值个数是( B )
A.1 B.2 C.3 D.4
19(全国Ⅰ3)已知向量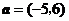 ,
,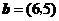 ,则
,则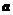 与
与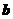 ( A )
( A )
A.垂直 B.不垂直也不平行 C.平行且同向 D.平行且反向
20(全国Ⅱ5)在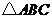 中,已知
中,已知 是
是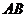 边上一点,若
边上一点,若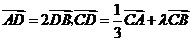 ,则
,则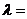 ( A )
( A )
A.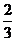 B.
B.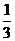 C.
C. D.
D.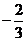
(三)解答题
1.(福建卷理17) 已知向量m=(sinA,cosA),n=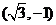 ,m·n=1,且A为锐角.
,m·n=1,且A为锐角.
(Ⅰ)求角A的大小;(Ⅱ)求函数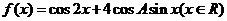 的值域.
的值域.
解:(Ⅰ) 由题意得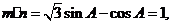
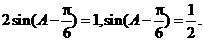
由A为锐角得 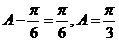
(Ⅱ) 由(Ⅰ)知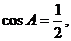
所以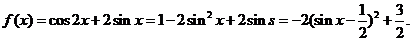
因为x∈R,所以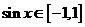 ,因此,当
,因此,当 时,f(x)有最大值
时,f(x)有最大值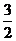 .
.
当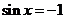 时,
时, 有最小值-3,所以所求函数
有最小值-3,所以所求函数 的值域是
的值域是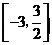
2.(福建卷文17)已知向量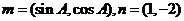 ,且
,且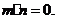
(Ⅰ)求tanA的值;(Ⅱ)求函数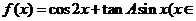 R)的值域.
R)的值域.
本小题主要考查平面向量的数量积计算、三角函数的基本公式、三角恒等变换、一元二次函数的最值等基本知识,考查运算能力,满分12分.
解:(Ⅰ)由题意得m·n=sinA-2cosA=0,因为cosA≠0,所以tanA=2.(Ⅱ)由(Ⅰ)知tanA=2得
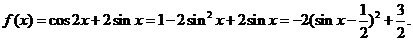 因为x
因为x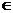 R,所以
R,所以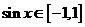 .当
.当 时,f(x)有最大值
时,f(x)有最大值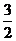 ,当sinx=-1时,f(x)有最小值-3,所以所求函数f(x)的值域是
,当sinx=-1时,f(x)有最小值-3,所以所求函数f(x)的值域是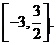
2007高考试题及解析
(二)填空题
1.(北京卷理10)已知向量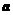 与
与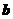 的夹角为
的夹角为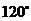 ,且
,且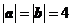 ,那么
,那么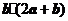 的值为
.
的值为
.
[标准答案]: 0
[试题分析]: 利用数形结合知,向量a与2a+b垂直。
[备考提示]: 向量的共线、平行、垂直、构成特殊三角形、特殊四边形等希望引起注意。
2.(北京卷文11)已知向量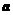 与
与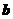 的夹角为
的夹角为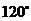 ,且
,且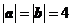 ,那么
,那么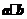 的值为
.
的值为
.
[答案]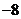
[解析]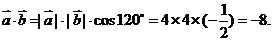
3.(江苏卷5)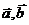 的夹角为
的夹角为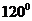 ,
,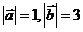 ,则
,则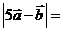 。
。
[解析]本小题考查向量的线性运算.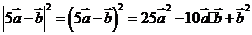
=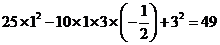 ,
,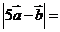 7
7
[答案]7
4.(江西卷理13)直角坐标平面上三点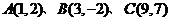 ,若
,若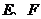 为线段
为线段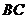 的三等分点,则
的三等分点,则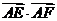 = .
= .
[答案]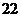 [解析]由已知得
[解析]由已知得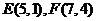 ,则
,则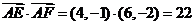
5.(江西卷文16)如图,正六边形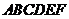 中,有下列四个命题:
中,有下列四个命题:
 A.
A.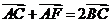
B.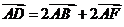
C.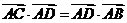
D.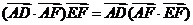
其中真命题的代号是 (写出所有真命题的代号).
[解析]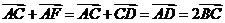 , ∴
, ∴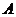 对取
对取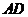 的中点
的中点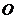 ,则
,则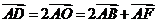 ,
,
∴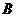 对设
对设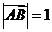 , 则
, 则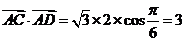 ,而
,而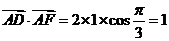 ,∴
,∴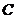 错
错
又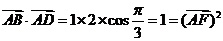 ,∴
,∴ 对∴真命题的代号是
对∴真命题的代号是
6.(陕西卷理15文15)关于平面向量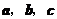 .有下列三个命题:
.有下列三个命题:
①若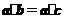 ,则
,则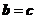 .②若
.②若 ,
,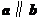 ,则
,则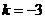 .③非零向量
.③非零向量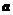 和
和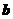 满足
满足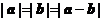 ,则
,则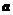 与
与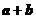 的夹角为
的夹角为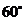 .其中真命题的序号为 .(写出所有真命题的序号)
.其中真命题的序号为 .(写出所有真命题的序号)
解:①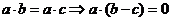 ,向量
,向量 与
与 垂直②
垂直②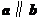

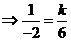
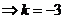
③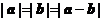
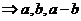 构成等边三角形,
构成等边三角形,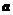 与
与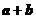 的夹角应为
的夹角应为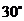 所以真命题只有②。
所以真命题只有②。
7.(上海卷理5文5)若向量(a、(b满足|(a|=1,|(b|=2,且(a与(b的夹角为,则|(a+(b|=
[答案]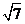
[解析]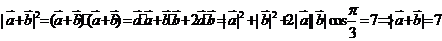 .
.
8. (天津卷理14)如图,在平行四边形
(天津卷理14)如图,在平行四边形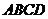 中,
中,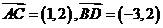 ,
,
则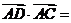 .
.
解析:令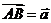 ,
,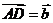 ,则
,则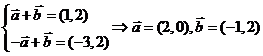
所以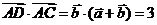 .
.
9.(天津卷文14)已知平面向量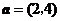 ,
,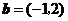 ,若
,若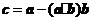 ,则
,则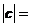 .
.
解析:因为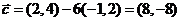 ,所以
,所以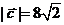 .
.
10.(浙江卷文16)已知 是平面内的单位向量,若向量
是平面内的单位向量,若向量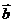 满足
满足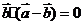 ,则
,则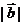 的取值范围是
。
的取值范围是
。
答案: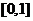

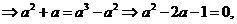
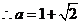 (舍负).
(舍负).
(一)选择题
1.(安徽理3文2)在平行四边形ABCD中,AC为一条对角线,若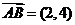 ,
,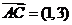 ,则
,则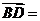 ( )
( )
A. (-2,-4) B.(-3,-5) C.(3,5) D.(2,4)
解:因为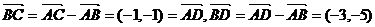 ,选B。
,选B。
2.(广东卷理8)在平行四边形 中,
中, 与
与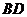 交于点
交于点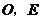 是线段
是线段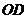 的中点,
的中点,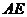 的延长线与
的延长线与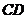 交于点
交于点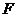 .若
.若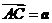 ,
,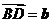 ,则
,则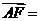 ( B )
( B )
A.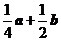 B.
B.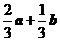 C.
C.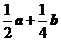 D.
D.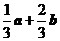
[解析]此题属于中档题.解题关键是利用平面几何知识得出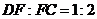 ,然后利用向量的加减法则易得答案B.
,然后利用向量的加减法则易得答案B.
3.(广东卷文3)已知平面向量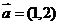 ,
,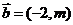 ,且
,且 //
//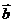 ,则
,则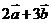 =( )
=( )
A、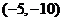 B、
B、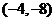 C、
C、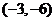 D、
D、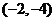
[解析]排除法:横坐标为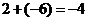 ,选B.
,选B.
4.(海南宁夏卷理8文9)平面向量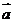 ,
,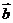 共线的充要条件是( )
共线的充要条件是( )
A. 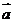 ,
,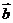 方向相同 B.
方向相同 B. 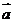 ,
,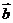 两向量中至少有一个为零向量
两向量中至少有一个为零向量
C. 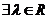 ,
, 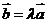 D.
存在不全为零的实数
D.
存在不全为零的实数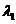 ,
,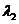 ,
,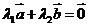
[试题解析]:若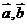 均为零向量,则显然符合题意,且存在不全为零的实数
均为零向量,则显然符合题意,且存在不全为零的实数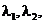 使得
使得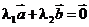 ;
; [解析]由定比分点的向量式得:
[解析]由定比分点的向量式得: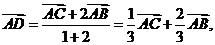
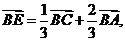
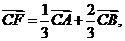 以上三式相加得
以上三式相加得
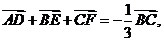 所以选A.
所以选A.
8.(辽宁卷理5)已知O,A,B是平面上的三个点,直线AB上有一点C,满足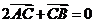 ,则
,则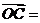 ( )
( )
A.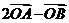 B.
B.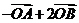 C.
C.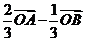 D.
D.
解析:本小题主要考查平面向量的基本定理。
依题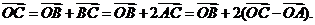 ∴
∴
 答案:A
答案:A
9.(辽宁卷文5)已知四边形 的三个顶点
的三个顶点 ,
,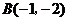 ,
,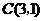 ,且
,且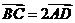 ,则顶点
,则顶点 的坐标为( )
的坐标为( )
A.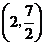 B.
B.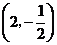 C.
C.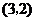 D.
D.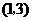
解析:本小题主要考查平面向量的基本知识。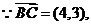
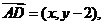
且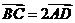 ,
,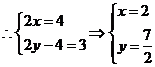 答案:A
答案:A
10.(全国Ⅰ卷理3文5)在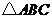 中,
中,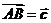 ,
,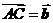 .若点
.若点 满足
满足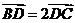 ,则
,则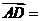
A.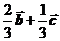 B.
B.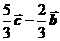 C.
C.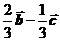 D.
D.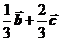
A. 由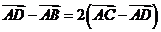 ,
,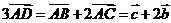 ,
,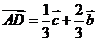 ;
;
11.(四川卷文3)设平面向量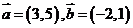 ,则
,则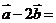 ( )
( )
(A)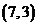 (B)
(B)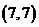 (C)
(C)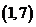 (D)
(D)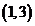
[解]:∵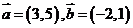 ∴
∴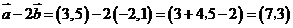
故选C;此题重点考察向量加减、数乘的坐标运算
12.(上海春卷13)已知向量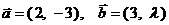 ,若
,若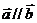 ,则
,则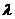 等于( )
等于( )
(A)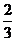 .
(B)
.
(B)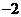 .
(C)
.
(C)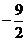 .
(D)
.
(D)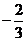
解析:由题意得2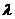 -(-3)3=0,所以
-(-3)3=0,所以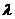 =
=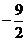 。
。
13.(湖南卷文7)在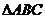 中,AB=3,AC=2,BC=
中,AB=3,AC=2,BC=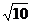 ,则
,则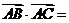 (
)
(
)
A.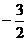 B.
B.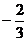 C.
C.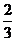 D.
D.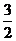
[答案]D
[解析]由余弦定理得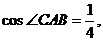 所以
所以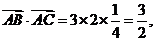 选D.
选D.
14.(浙江卷理9)已知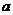 ,b是平面内两个互相垂直的单位向量,若向量
,b是平面内两个互相垂直的单位向量,若向量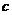 满足
满足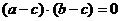 ,则
,则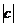 的最大值是
的最大值是
(A)1 (B)2
(C)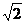 (D)
(D)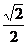
解析:本小题主要考查向量的数量积及向量模的相关运算问题。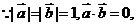
展开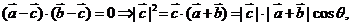
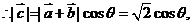 则
则 的最大值是
的最大值是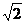 ;
;
或者利用数形结合,  ,
,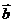 对应的点A,B在圆
对应的点A,B在圆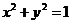 上,
上,
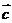 对应的点C在圆
对应的点C在圆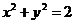 上即可.
上即可.
17. (安徽卷理5)将函数
(安徽卷理5)将函数 的图象按向量
的图象按向量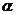 平移后所得的图象关于点
平移后所得的图象关于点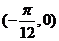 中心对称,则向量
中心对称,则向量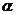 的坐标可能为( )
的坐标可能为( )
A.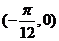 B.
B.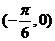 C.
C.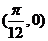 D.
D.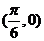
解:设平移向量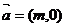 ,则函数按向量平移后的表达式为
,则函数按向量平移后的表达式为
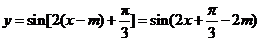 ,因为图象关于点
,因为图象关于点 中心对称,
中心对称,
故 代入得:
代入得: 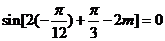 ,
,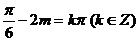 ,
,
k=0得: ,选C。本题也可以从选择支出发,逐个排除也可。
,选C。本题也可以从选择支出发,逐个排除也可。
18.(福建卷理9)函数f(x)=cosx(x)(x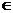 R)的图象按向量(m,0) 平移后,得到函数y=-f′(x)的图象,则m的值可以为
R)的图象按向量(m,0) 平移后,得到函数y=-f′(x)的图象,则m的值可以为
A.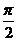 B.
B.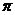 C.-
C.-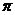 D.-
D.- 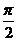
解: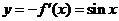 ,而
,而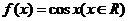 的图象按向量
的图象按向量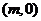 平移后
平移后
得到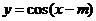 ,所以
,所以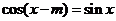 ,故
,故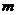 可以为
可以为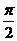 .
.
19.(福建卷文7)函数y=cosx(x∈R)的图象向左平移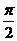 个单位后,得到函数y=g(x)的图象,则g(x)的解析式为
个单位后,得到函数y=g(x)的图象,则g(x)的解析式为
A.-sinx B.sinx C.-cosx D.cosx
解: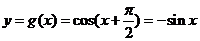
20.(湖北卷理5文7)将函数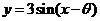 的图象F按向量
的图象F按向量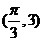 平移得到图象
平移得到图象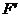 ,若
,若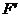 的一条对称轴是直线
的一条对称轴是直线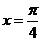 ,则
,则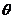 的一个可能取值是
的一个可能取值是
A.  B.
B.
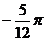 C.
C.
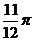 D.
D.

解: 平移得到图象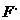 的解析式为
的解析式为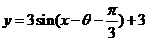 ,
,
对称轴方程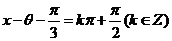 ,
,
把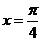 带入得
带入得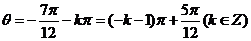 ,令
,令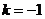 ,
,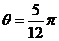
21.(辽宁卷理8文8)将函数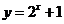 的图象按向量
的图象按向量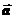 平移得到函数
平移得到函数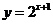 的图象,则
的图象,则
A.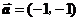 B.
B.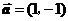 C.
C.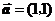 D.
D.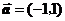
答案:A
解析:本小题主要考查函数图像的平移与向量的关系问题。依题由函数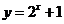 的图象得到函数
的图象得到函数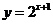 的图象,需将函数
的图象,需将函数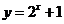 的图象向左平移1个单位,向下平移1个单位;故
的图象向左平移1个单位,向下平移1个单位;故
22.(重庆卷理7)若过两点P1(-1,2),P2(5,6)的直线与x轴相交于点P,则点P分有向线段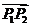 所成的比
所成的比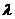 的值为
的值为
(A)-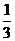 (B)
-
(B)
-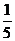 (C)
(C)
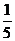 (D)
(D)
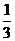
解:设点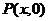 ,则
,则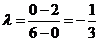 ,选 A
,选 A
23.(重庆卷文4)若点P分有向线段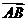 所成的比为-
所成的比为-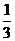 ,则点B分有向线段
,则点B分有向线段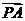 所成的比是
所成的比是
(A)-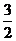 (B)-
(B)-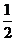 (C)
(C)
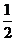 (D)3
(D)3
[答案]A
[解析]本小题主要考查线段定比分点的有关计算。如下图可知,B点是有向线段PA的外分点,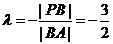 ,故选A。
,故选A。
1.(2009广东卷理)若平面向量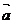 ,
,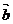 满足
满足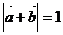 ,
, 平行于
平行于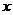 轴,
轴,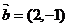 ,则
,则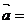 .
.
[解析]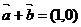 或
或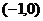 ,则
,则
或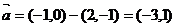 .
.
2.(2009江苏卷)已知向量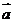 和向量
和向量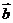 的夹角为
的夹角为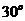 ,
,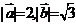 ,
,
则向量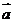 和向量
和向量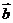 的数量积
的数量积 = 。
= 。
[解析] 考查数量积的运算。 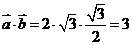
3.(2009安徽理)给定两个长度为1的平面向量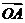 和
和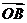 ,
,
它们的夹角为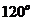 .如图所示,点C在以O为圆心的圆弧
.如图所示,点C在以O为圆心的圆弧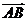
上变动. 若
若 其中
其中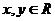 ,则
,则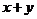
的最大值是________.
[解析]设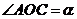
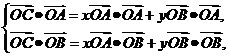 ,即
,即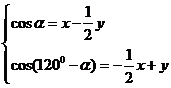
∴
4.(2009安徽文)在平行四边形ABCD中,E和F分别是边CD和BC的中点,或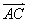 =
=
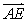 +
+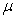
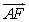 ,其中
,其中 ,
,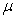
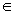 R ,则
R ,则 +
+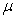 = ______。
= ______。 

[解析]设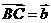 、
、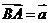 则
则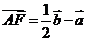 ,
,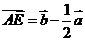 ,
,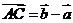 代入条件得
代入条件得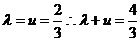 [答案]4/3
[答案]4/3
5.(2009江西卷文)已知向量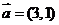 ,
,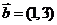 ,
,
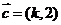 ,若
,若 则
则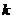 =
.
=
.
答案: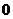 [解析]因为
[解析]因为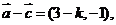 所以
所以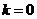 .
.
6.(2009江西卷理)已知向量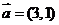 ,
,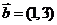 ,
,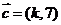 ,若
,若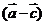 ∥
∥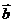 ,则
,则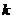 =
.
=
.
答案: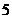 [解析]
[解析]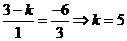
7.(2009湖南卷文)如图2,两块斜边长相等的直角三角板拼在一起,若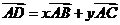 ,则
,则 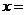
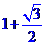 ,
,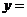
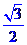 .
.
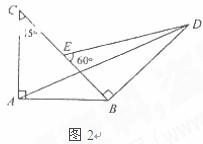
解:作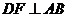 ,设
,设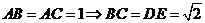 ,
,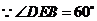 ,
,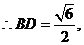
由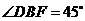 解得
解得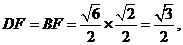 故
故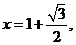
8.(2009辽宁文)在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为___________.



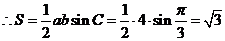
2(2009湖南卷文)(每小题满分12分) 已知向量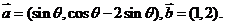
(Ⅰ)若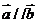 ,求
,求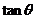 的值;
(Ⅱ)若
的值;
(Ⅱ)若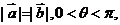 求
求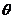 的值。
的值。
解:(Ⅰ) 因为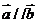 ,所以
,所以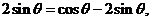 于是
于是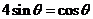 ,故
,故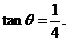
(Ⅱ)由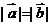 知,
知,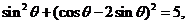 所以
所以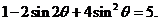
从而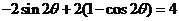 ,即
,即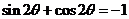 ,于是
,于是 .又由
.又由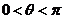 知,
知,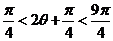 ,所以
,所以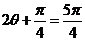 ,或
,或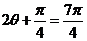 .因此
.因此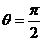 ,或
,或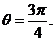
3(2009广东文理)已知向量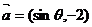 与
与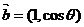 互相垂直,其中
互相垂直,其中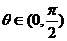 .(1)求
.(1)求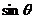 和
和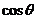 的值;(2)若
的值;(2)若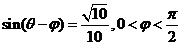 ,求
,求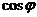 的值.
的值.
解:(1)∵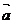 与
与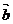 互相垂直,则
互相垂直,则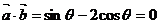 ,即
,即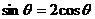 ,代入
,代入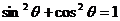 得
得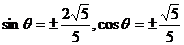 ,又
,又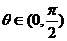 ,∴
,∴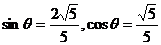 .
.
(2)∵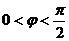 ,
,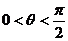 ,∴
,∴ ,则
,则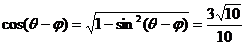 ,∴
,∴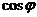
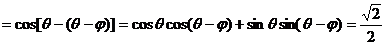 .
.
4.2009江苏卷)设向量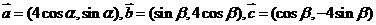
(1)若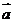 与
与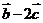 垂直,求
垂直,求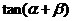 的值;(2)求
的值;(2)求 的最大值;
的最大值;
(3)若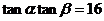 ,求证:
,求证: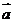 ∥
∥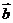 .
. 
 2008高考试题及解析
2008高考试题及解析
23.(2009重庆卷理)已知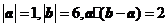 ,则向量
,则向量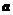 与向量
与向量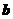 的夹角是( )
的夹角是( )
A.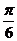 B.
B.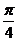 C.
C.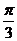 D.
D.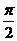


[答案]C
22.(2009福建卷文)设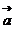 ,
,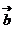 ,
,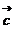 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足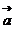 与
与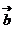 不共线,
不共线,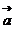
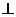
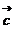 ∣
∣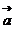 ∣=∣
∣=∣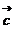 ∣,则∣
∣,则∣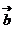 •
•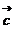 ∣的值一定等于
∣的值一定等于 

A.以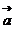 ,
,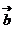 为邻边的平行四边形的面积
B. 以
为邻边的平行四边形的面积
B. 以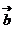 ,
,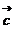 为两边的三角形面积
为两边的三角形面积
C.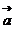 ,
,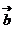 为两边的三角形面积
D. 以
为两边的三角形面积
D. 以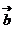 ,
,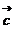 为邻边的平行四边形的面积
为邻边的平行四边形的面积
解析 假设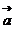 与
与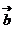 的夹角为
的夹角为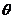 ,∣
,∣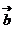 •
•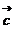 ∣=︱
∣=︱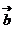 ︱·︱
︱·︱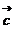 ︱·∣cos<
︱·∣cos<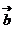 ,
,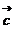 >∣=︱
>∣=︱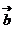 ︱·︱
︱·︱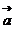 ︱•∣cos(90
︱•∣cos(90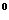
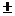
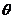 )∣=︱
)∣=︱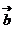 ︱·︱
︱·︱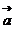 ︱•sin
︱•sin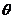 ,即为以
,即为以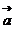 ,
,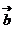 为邻边的平行四边形的面积,故选A。
为邻边的平行四边形的面积,故选A。
21.(2009湖南卷理)对于非0向量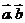 ,
,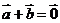 是“
是“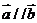 ”的(
)
”的(
)
A.充分不必要条件 B. 必要不充分条件C.充分必要条件 D. 既不充分也不必要条件
[答案]:A
[解析]由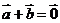 可得
可得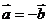 ,即得
,即得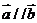 ,但
,但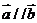 ,不一定
,不一定
有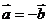 ,所以“
,所以“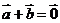 ”是“
”是“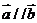 的充分不必要条件。
的充分不必要条件。
18.(2009全国卷Ⅰ文)设非零向量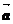 、
、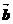 、
、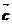 满足
满足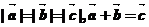 ,则
,则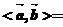 ( )
( )
(A)150°B)120° (C)60° (D)30°
[解析]本小题考查向量的几何运算、考查数形结合的思想,基础题。
 (A)
(A) (B)
(B)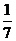 (C)
(C)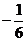 (D)
(D)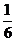
[答案]A
[解析]向量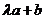 =(-3
=(-3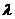 -1,2
-1,2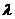 ),
),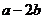 =(-1,2),因为两个向量垂直,故有(-3
=(-1,2),因为两个向量垂直,故有(-3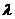 -1,2
-1,2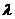 )×(-1,2)=0,即3
)×(-1,2)=0,即3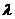 +1+4
+1+4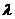 =0,解得:
=0,解得: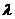 =
= ,故选.A。
,故选.A。
17.(2009辽宁卷文)平面向量a与b的夹角为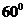 ,a=(2,0), | b |=1,则 | a+2b |=
,a=(2,0), | b |=1,则 | a+2b |=
(A)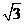 (B)2
(B)2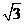 (C)4 (D)12
(C)4 (D)12
[解析]由已知|a|=2,|a+2b|2=a2+4a·b+4b2=4+4×2×1×cos60°+4=12 ∴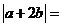
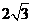
[答案]B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com