
2.已知定义在 上的奇函数
上的奇函数 ,当
,当 时,
时,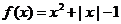 ,
,
那么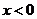 时,
时,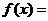 .
.
1.函数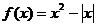 的单调递减区间是____________________。
的单调递减区间是____________________。
6.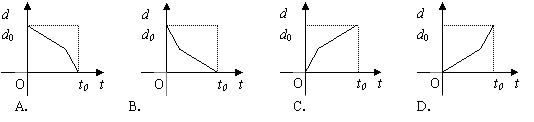 某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程. 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程. 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
5.下列四个命题:(1)函数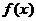 在
在 时是增函数,
时是增函数,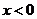 也是增函数,所以
也是增函数,所以 是增函数;(2)若函数
是增函数;(2)若函数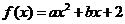 与
与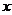 轴没有交点,则
轴没有交点,则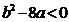 且
且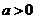 ;(3)
;(3) 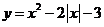 的递增区间为
的递增区间为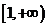 ;(4)
;(4) 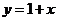 和
和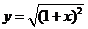 表示相等函数。
表示相等函数。
其中正确命题的个数是( )
A.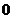 B.
B. C.
C.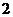 D.
D.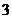
4.已知函数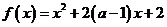 在区间
在区间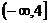 上是减函数,
上是减函数,
则实数 的取值范围是( )
的取值范围是( )
A.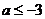 B.
B.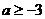 C.
C.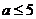 D.
D.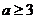
3.函数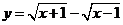 的值域为( )
的值域为( )
A.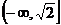 B.
B.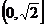
C.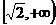 D.
D.
2.若函数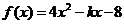 在
在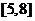 上是单调函数,则
上是单调函数,则 的取值范围是( )
的取值范围是( )
A.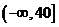 B.
B.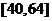
C.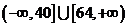 D.
D.
1.下列判断正确的是( )
A.函数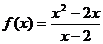 是奇函数
B.函数
是奇函数
B.函数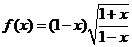 是偶函数
是偶函数
C.函数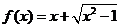 是非奇非偶函数 D.函数
是非奇非偶函数 D.函数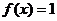 既是奇函数又是偶函数
既是奇函数又是偶函数
4.已知函数 .
.
① 当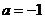 时,求函数的最大值和最小值;
时,求函数的最大值和最小值;
② 求实数 的取值范围,使
的取值范围,使 在区间
在区间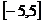 上是单调函数。
上是单调函数。
(数学1必修)第一章(下) 函数的基本性质
[综合训练B组]
3.利用函数的单调性求函数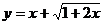 的值域;
的值域;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com