
3.三角函数式的化简



常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数.



(1)降幂公式



 ;
;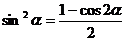 ;
;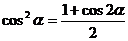 。
。



(2)辅助角公式
 ,
,



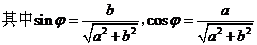 。
。



[名师点睛]1.两角和与差的三角函数
 ;
;



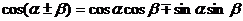 ;
; 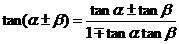 。
。



2.二倍角公式



 ;
;


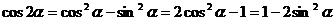 ;
; 
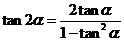 。
。



[名师点睛]诱导公式用角度和弧度制表示都成立,记忆方法可以概括为“奇变偶不变,符号看象限”,“变”与“不变”是相对于对偶关系的函数而言的,sinα与cosα对偶,“奇”、“偶”是对诱导公式中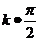 +α的整数k来讲的,象限指
+α的整数k来讲的,象限指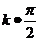 +α中,将α看作锐角时,
+α中,将α看作锐角时,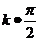 +α所在象限,如将cos(
+α所在象限,如将cos(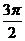 +α)写成cos(
+α)写成cos(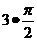 +α),因为3是奇数,则“cos”变为对偶函数符号“sin”,又
+α),因为3是奇数,则“cos”变为对偶函数符号“sin”,又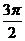 +α看作第四象限角,cos(
+α看作第四象限角,cos(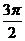 +α)为“+”,所以有cos(
+α)为“+”,所以有cos(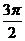 +α)=sinα。
+α)=sinα。
[试题演练]化简:(1)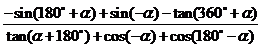 ;
;
(2)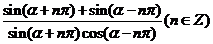 。
。
解:(1)原式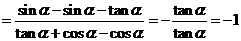 ;
;
(2)①当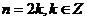 时,原式
时,原式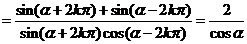 。
。
②当 时,原式
时,原式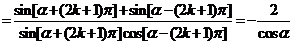 。
。
点评:关键抓住题中的整数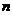 是表示
是表示 的整数倍与公式一中的整数
的整数倍与公式一中的整数 有区别,所以必须把
有区别,所以必须把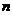 分成奇数和偶数两种类型,分别加以讨论.
分成奇数和偶数两种类型,分别加以讨论.
[名师点睛]同角三角函数的关系有平方关系和商数关系,用同角三角函数定义反复证明强化记忆,在解题时要注意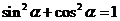 ,这是一个隐含条件,在解题时要经常能想到它。利用同角的三角函数关系求解时,注意角所在象限,看是否需要分类讨论。
,这是一个隐含条件,在解题时要经常能想到它。利用同角的三角函数关系求解时,注意角所在象限,看是否需要分类讨论。
[试题演练]若 则
则 =(
)
=(
)
(A) (B)2
(C)
(B)2
(C)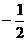 (D)
(D)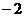

解:由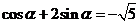 可得:由
可得:由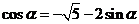 ,
,
又由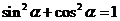 ,可得:
,可得: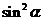 +(
+(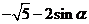 )2=1
)2=1
可得 =-
=-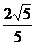 ,
,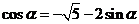 =-
=-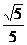 ,所以,
,所以, =
=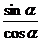 =2。
=2。
点评:对于给出正弦与余弦的关系式的试题,要能想到隐含条件: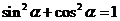 ,与它联系成方程组,解方程组来求解。
,与它联系成方程组,解方程组来求解。
8、复读全文,验证答案
将初次改错后的短文再次读,检查并验证所做的答案是否能使全文语气贯通、流畅,行文逻辑发展是否合乎情理,全篇结构是否严谨完整等。复读过程中,凡遇到不能之处,须进一步进行细致的推敲,以便使答案更有把握。
总之,只要我们掌握了正确的语言规则和答题技巧,用正确的语言武装自己,这样,文章出现的任何错误都难逃出你的“火眼金睛”。
7、仔细推敲,切忌画蛇添足
众所周知,一种意思可以用多种语言形式来表达,英语也不例外。这就要求我们,尤其是英语基础好的同学牢牢记往指导语中“原行没错的,请不要改”这一关键注释;千万不要用自认为比原文更好的表达法来改正文中本来没有任何错误的句子,这一现象曾在历年的高考中出现过。
6、根据不同的错误,分别进行解题。大小写和拼写是否正确等。
5、根据词法、句法知识,检查和判断错误所在,这是最关键的一步。可逐句检查主谓是否一致,代词、关联词的使用是正确,动词形式是相当,词语之间的反革命配是否正确,表达是否惯用法。大小写和拼写是否正确等。
4、对照上下文,分析句意
弄清清上下文之间的联系及其逻辑关系,逐行逐句检查句子的结构是否完整,语气是否连贯,是否有与短文的中心意思不相符的现象。
3、通语全文,弄清在大意
首先把全文浏览一遍,了解全文大意,留心短文中关键的词语,为下一步判断和改错奠定基础。
短文改错,每行不会超过一个错误,有的同学似乎认为弄清主旨,意义不大,因而只把注意力放在语法和单词上,忽视了对文章大意的理解。看到了自己认为“错误”的地方,就急于提笔改动,结果只见树木不见森林,旧错没改犯新错。同学们必须明确,在很多情况下,判断错误不能只从某个单词的本身,甚至不能从整个句子的本身去看,而要从上下文,甚至从整篇文章去看。只有通晓全文的结构,即从整体到局部,再从局部到整体,才能在最后作出判断:此行是否有错误,如果有错误是缺词、多词,还是错词,如果是错词属哪方面,是语法错误、逻辑错误还是其它错误?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com