
4.下列取代基或微粒中,碳原子都满足最外层为8电子结构的是( )
A.乙基(-CH2CH3) B.碳正离子[(CH3)3C⊕]
C.碳化钙 (CaC2) D.碳烯 (:CH2)
3.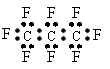 最近美国宇航局(NASA)马里诺娃博士找到了一种比二氧化碳有效104倍的“超级温室气体”-全氟丙烷(C3F8),并提出用其“温室化火星”使其成为第二个地球的计划。有关全氟丙烷的说法正确的是
( )
最近美国宇航局(NASA)马里诺娃博士找到了一种比二氧化碳有效104倍的“超级温室气体”-全氟丙烷(C3F8),并提出用其“温室化火星”使其成为第二个地球的计划。有关全氟丙烷的说法正确的是
( )
A、分子中三个碳原子可能处于同一直线上 B、全氟丙烷的电子式为:
C、相同压强下,沸点:C3F8<C3H8
D、全氟丙烷分子中既有极性键又有非极性键
2.据央视报道,自2006年12月1日起在武汉九市进行车用乙醇汽油封闭推广行动。车用
乙醇汽油是把变性燃料乙醇和汽油按一定比例混配形成的一种新型汽车燃料。经多项检
测结果表明,它不影响汽车的行驶性能,还可以减少有害气体的排放量。在美国、巴西
等国早已推广使用。下列有关乙醇汽油的说法正确的是( )
A.乙醇汽油是一种纯净物
B.乙醇汽油作燃料不会产生碳氧化物等有害气体,其优点是可以减少对环境的污染
C.乙醇和汽油都可作溶剂,也可相互溶解
D.乙醇和乙二醇互为同系物
1.2007年下半年,我国接连发生多起煤矿爆炸事故,造成重大人员伤亡和财产损失。煤矿发生爆炸事故的元凶是煤矿坑道气中含有的甲烷。下列关于甲烷的叙述中错误的是( )
A.甲烷分子是一种呈正四面体型的、含极性键的非极性分子
B.甲烷分子中两个氢原子被氯取代后,可形成两种不同结构的分子
C.甲烷是重要的化工原料,其分解产物可用于合成氨和橡胶工业
D.“抽”出坑道中的甲烷,既可用作清洁燃料,又可防止爆炸
3、注意解三角形中的应用题,应用题是数学的一个难点,平时应加强训练。
[母题特供]每个专题5道最典型试题
母题一:
金题引路:已知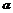 ∈
∈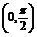 ,
,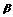 ∈
∈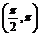 且sin(
且sin(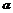 +
+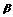 )=
)=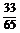 ,cos
,cos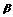 =-
=-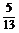 .求sin
.求sin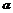 .
.
解 ∵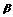 ∈
∈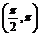 ,cos
,cos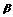 =-
=-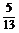 ,∴sin
,∴sin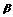 =
=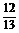 .又∵0<
.又∵0<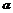 <
<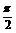 ,
,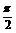 <
<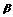 <
<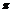 ,∴
,∴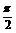 <
<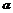 +
+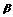 <
<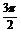 ,
,
又sin(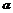 +
+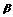 )=
)=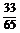 ,∴
,∴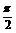 <
<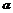 +
+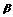 <
<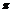 ,cos(
,cos(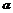 +
+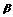 )=-
)=-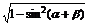 =-
=-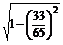 =-
=-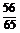 ,
,
∴sin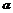 =sin[(
=sin[(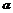 +
+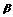 )-
)-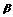 ]=sin(
]=sin(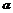 +
+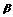 )cos
)cos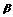 -cos(
-cos(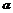 +
+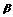 )sin
)sin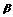 =
=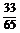 ·
·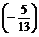 -
-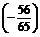 ·
·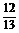 =
=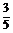
母题二:
金题引路:在△ABC中,角A、B、C所对边分别是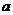 、
、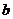 、
、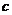 ,且
,且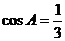 .
(1)求
.
(1)求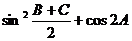 的值; (2)若
的值; (2)若 ,求
,求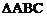 面积的最大值.
面积的最大值.
解:(1)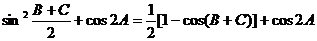
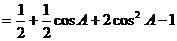
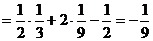
(2)由余弦定理得: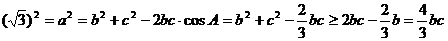 .
.
∴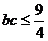 当且仅当
当且仅当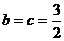 时,
时,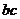 有最大值
有最大值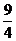 ∴
∴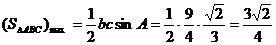
母题三:
金题引路:已知 ,
,
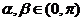 (1)求
(1)求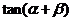 的值;(2)求函数
的值;(2)求函数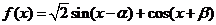 的最大值.
的最大值.
解:(1)由
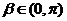 得
得 ,
,
于是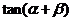 =
=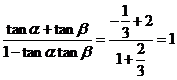 .
.
(2)因为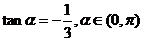 所以
所以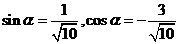


 的最大值为
的最大值为 .
.
母题四:
金题引路:已知函数f(x)=Asin(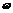 x+
x+ )(A>0,
)(A>0, 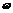 >0,|
>0,| |<
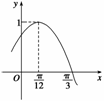
|<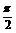 ) (x∈R)的部分图象如图所示.
) (x∈R)的部分图象如图所示.
 (1)求f(x)的表达式;(2)设g(x)=f(x)-
(1)求f(x)的表达式;(2)设g(x)=f(x)- f
f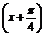 ,
,
求函数g(x)的最小值及相应的x的取值集合.
解 (1)由图象可知:A=1,函数f(x)的周期T满足: =
=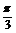 -
- =
=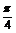 ,T=
,T=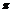 ,
,
∴T= =
=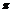 .∴
.∴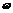 =2.∴f(x)=sin(2x+
=2.∴f(x)=sin(2x+ ).又f(x)图象过点
).又f(x)图象过点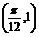 ,
,
∴f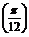 =sin
=sin =1,
=1,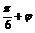 =2k
=2k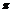 +
+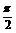 (k∈Z).又|
(k∈Z).又| |<
|<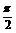 ,故
,故 =
=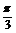 .∴f(x)=sin
.∴f(x)=sin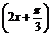 .
.
(2)方法一 g(x)=f(x)- f
f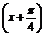 =sin
=sin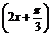 -
- sin
sin =sin
=sin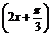 -
- sin
sin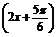
=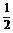 sin2x+
sin2x+ cos2x+
cos2x+ sin2x-
sin2x- cos2x=2sin2x,由2x=2k
cos2x=2sin2x,由2x=2k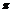 -
-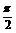 (
(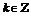 ),得x=k
),得x=k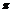 -
-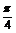 (
(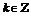 ),
),
∴g(x)的最小值为-2,相应的x的取值集合为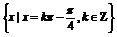
方法二
g(x)=f(x)- f
f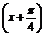 =sin
=sin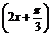 -
- sin
sin =sin
=sin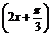 -
- cos
cos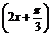
=2sin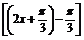 =2sin2x,由2x=2k
=2sin2x,由2x=2k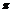 -
-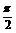 (
( ),得x=k
),得x=k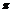 -
-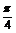 (
( ),
),
∴g(x)的最小值为-2,相应的x的取值集合为{x|x=k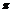 -
-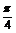 ,
, }.
}.
母题五、
金题引路:某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度 (米)随着时间
(米)随着时间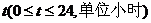 而周期性变化,每天各时刻
而周期性变化,每天各时刻 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
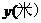 |
1.0 |
1.4 |
1.0 |
0.6 |
1.0 |
1.4 |
0.9 |
0.5 |
1.0 |
(Ⅰ)试画出散点图;(Ⅱ)观察散点图,从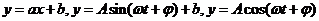 中选择一个合适的函数模型,并求出该拟合模型的解析式;(Ⅲ)如果确定在白天7时~19时当浪高不低于0。8米时才进行训练,试安排恰当的训练时间。
中选择一个合适的函数模型,并求出该拟合模型的解析式;(Ⅲ)如果确定在白天7时~19时当浪高不低于0。8米时才进行训练,试安排恰当的训练时间。
解:(1)
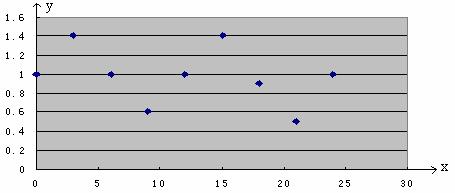
(2)由(1)知选择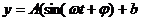 较合适。
较合适。
由图知,A=0.4,b=1,T=12,
所以, ,把t=0,y=1代入
,把t=0,y=1代入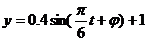 ,
,
得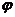 =0,所以,所求的解析式为:
=0,所以,所求的解析式为: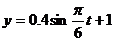 (0≤t≤24)。
(0≤t≤24)。
(3)由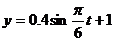 ≥0.8,得
≥0.8,得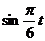 ≥-
≥- 。,
。,
则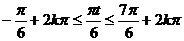 (k
(k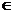 Z),
Z),
即12k-1≤t≤12k+7,所以,0≤t≤7或11≤t≤19或23≤t≤24
答:应安排在11时到19时训练较恰当。
2、注意知识之间的横向联系,三角函数知识之间的联系,三角函数与其它知识的联系,如三角函数与向量等。
1、本节公式较多,但都是有规律的,认真总结规律,记住公式是解答三角函数的关键。
5.高考考点分析
近几年高考中,三角函数主要以选择题和解答题的形式出现。主要考察内容按综合难度分,我认为有以下几个层次:
第一层次:通过诱导公式和倍角公式的简单运用,解决有关三角函数基本性质的问题。如判断符号、求值、求周期、判断奇偶性等。
第二层次:三角函数公式变形中的某些常用技巧的运用。如辅助角公式、平方公式逆用、切弦互化等。
第三层次:充分利用三角函数作为一种特殊函数的图象及周期性、奇偶性、单调性、有界性等特殊性质,解决较复杂的函数问题。如分段函数值,求复合函数值域等。
复习建议
4.解答三角高考题的策略。(1)发现差异:观察角、函数运算间的差异,即进行所谓的“差异分析”。
(2)寻找联系:运用相关公式,找出差异之间的内在联系。(3)合理转化:选择恰当的公式,促使差异的转化。
3.证明三角不等式的方法:比较法、配方法、反证法、分析法,利用函数的单调性,利用正、余弦函数的有界性,利用单位圆三角函数线及判别法等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com