
(一)福建改革开放成就与原因、YU到的困难与政府职能
材料一:福建省2008年经济和和社会发展状况
|
|
2008年 |
备注 |
|
全社会固定资产投资 |
5286.82亿元 |
比上年增长22.3%,其中,城镇投资增长21.2%,农村投资增长32.1%。 |
|
生产总值 |
全省10823.11亿元,人均地区生产总值30123元 |
分别增长13.0%和12.2%。 |
|
万元生产总值能耗与排污 |
能耗0.843吨标准煤,化学需氧量排放量37.82万吨,二氧化硫排放量42.89万吨 |
分别比上年下降3.7%,1.30%,3.77%,完成了年度节能减排目标。 |
|
财政总收入 |
些1516.33亿元 |
比上年增长18.2% |
|
农民人均纯收入和城镇居民人均可支配收入 |
分别为6196元和17961.45元 |
扣除价格因素,分别实际增长和8.3%和10.8%, |
|
三次产业结构 |
由2007年的10.8∶49.2∶40.0转为10.7∶50.0∶39.3 |
三次产业增加值分别为1157.75亿元、5415.77亿元、4249.59亿元,分别增长4.8%、15.2%、12.1%。 |
|
就业 |
全省从业人员2089.47万人 |
比上年末增加74.14万人。 |
|
进出口 |
进出口总额848.32亿美元,出口569.86亿美元,进口278.46亿美元。 |
进出口总额比上年增长13.9%。出口与进品增长分别比上年14.1%和增长13.6%。对主要贸易伙伴进出口有不同程度发展。 |
注:2008年,①福建省人均GDP还落后于中等发达国家,节能减排指标还远远高于中等发达国家。厦门、福州、泉州在全国113个环保重点城市中分别位列第25位、第22位和第9位。
②农村和城镇居民家庭恩格尔系数分别为46.4%和40.6%。
③进出口总额相差较大。
④2008年末城镇登记失业率为3.86%,比上年末下降0.03个百分点。
(1)指出图表中福建省改革开放以来取得一系列成就及经济方面的原因(此为一般性道理,要记住)
答:①福建省生产总值和财政收入大幅度增长,经济增长迅速。②城乡居民收入不断增长,生活水平不断提高。③就业和社会保障水平不断提升,社会事业全面协调发展。④投资力度不断加大,促进城乡协调发展。⑤三次产业日趋合理,经济结构不断完善。⑥节能减排成就明显,生态环境质量不断提高。⑦进出口总额连年增长,对外开放水平不断提高。
原因:①坚持公有制为主体、多种所有制经济共同发展的基本经济制度,解放和发展生产力。②坚持按劳分配为主体、多种分配方式并存的分配制度,拓宽增收途径。③坚持市场调节与宏观调控相结合,建立和完善了社会主义市场经济体制,促进经济发展。④坚持以人为本、全面协调可持续的科学发展观,促进城乡、区域、人与自然、经济与社会、当前与长远等协调发展。⑤坚持经济体制改革,坚持对外开放基本国策。(如果单纯讲农村要加上:坚持和完善家庭联产承包责任制,调动农民的生产积极性,解放和发展农村社会生产力。)
(2)结合 “注”中存在的问题,就政府如何组织社会主义经济建设职能提出若干建议。
答:①坚持对人民负责的原则,加强经济调节。综合运用宏观调控手段促进节能减排,促进自主创新;加大对农村支持力度,统筹城乡发展,促进农民增收,提高农村居民消费水平;调整和优化进出口结构,推动产业升级,促进国民经济又好又快发展。②坚持依法行政,加强市场监管。依法加强对企业生产和经营的监督和管理,加强节能减排责任制,维护生态环境。③坚持为人民服务宗旨和求真务实精神,加强社会管理和公共服务,创设良好就业环境,增加就业;加强生态保护,促进人民生活质量提高。
(3)由于国际金融危机的影响,2008年福建省批准设立外商直接投资项目1101个,比上年下降36.1%。按历史可比口径统计,合同外资金额114.15亿美元,下降7.5%;按验资口径统计,合同外资金额71.52亿美元,下降24.3%。对外承包工程完成营业额1.33亿美元,下降35.6%;对外劳务合作完成营业额2.67亿美元,下降15.9%。据此有人认为,我国对外投资风险大,实行“走出去”战略时机不成熟,应重在“引进来”。请从唯物辩证法角度加以评析。
答:①联系具有普遍性、客观性和多样性。由于国际金融危机的影响,2008年福建省外商直接投资和对外承包工程、对外劳务合作总额同比有所下降,“引进来”与“走出去”都YU到一定的困难。②发展是前进性和曲折性的统一(或矛盾具有特殊性)。2008年福建省对外开放中YU到的困难是前进中的YU到问题,不能因此产生悲观心理。③事物是对立面的统一,矛盾双方相互依存、相互促进,并在一定条件下相互转化。“引进来”与“走出去”要相结合,共同推动开放型经济发展。④发展是量变和质变的统一。改革开放以来我国经济实力和综合国力不断增强,“走出去”战略是成熟的。
(4)福建省委2008年在总结海峡西岸经济区建设实践经验的基础上,提出了“重在持续、重在提升、重在运作、重在实效”的战略部署。这隐含文化创新的哪些道理?
答:①文化源于社会实践,社会实践是文化创新的源泉和动力。福建省委提出的“四个重在”的战略部署是根据海峡西岸经济区建设实践深入基础上总结的新经验。②文化创新可以推动社会实践的发展,推动社会实践的发展是文化创新的根本目的。福建省委提出“四个重在”的战略部署将进一步推动海峡西岸经济区建设。③文化创新是在文化继承基础上的文化发展,要顺应社会发展,坚持时代性和先进性,福建省委提出“四个重在”的战略部署体现文化与社会的与时俱进。
(三)解答题(共1题)
1.(福建卷文20)已知{an}是正数组成的数列,a1=1,且点(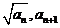 )(n
)(n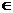 N*)在函数y=x2+1的图象上.
N*)在函数y=x2+1的图象上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若列数{bn}满足b1=1,bn+1=bn+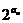 ,求证:bn ·bn+2<b2n+1.
,求证:bn ·bn+2<b2n+1.
本小题考查等差数列、等比数列等基本知识,考查转化与化归思想,推理与运算能力.
解法一:
(Ⅰ)由已知得an+1=an+1、即an+1-an=1,又a1=1,
所以数列{an}是以1为首项,公差为1的等差数列.
故an=1+(a-1)×1=n.
(Ⅱ)由(Ⅰ)知:an=n从而bn+1-bn=2n.bn=(bn-bn-1)+(bn-1-bn-2)+···+(b2-b1)+b1
=2n-1+2n-2+···+2+1= =2n-1.
=2n-1.
因为bn·bn+2-b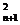 =(2n-1)(2n+2-1)-(2n-1-1)2=(22n+2-2n+2-2n+1)-(22n+2-2-2n+1-1)=-5·2n+4·2n
=(2n-1)(2n+2-1)-(2n-1-1)2=(22n+2-2n+2-2n+1)-(22n+2-2-2n+1-1)=-5·2n+4·2n
=-2n<0,所以bn·bn+2<b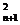 ,
,
解法二:(Ⅰ)同解法一.
(Ⅱ)因为b2=1,bn·bn+2- b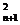 =(bn+1-2n)(bn+1+2n+1)-
b
=(bn+1-2n)(bn+1+2n+1)-
b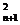 =2n+1·bn-1-2n·bn+1-2n·2n+1=2n(bn+1-2n+1)=2n(bn+2n-2n+1)=2n(bn-2n)=…=2n(b1-2)=-2n〈0,所以bn-bn+2<b2n+1
=2n+1·bn-1-2n·bn+1-2n·2n+1=2n(bn+1-2n+1)=2n(bn+2n-2n+1)=2n(bn-2n)=…=2n(b1-2)=-2n〈0,所以bn-bn+2<b2n+1
1.(海南宁夏卷理17)已知数列 是一个等差数列,且
是一个等差数列,且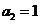 ,
, 。
。
(1)求 的通项
的通项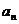 ;(2)求
;(2)求 前n项和
前n项和 的最大值。
的最大值。
解:(Ⅰ)设 的公差为
的公差为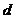 ,由已知条件,
,由已知条件, ,解出
,解出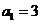 ,
,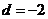 .
.
所以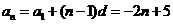 .
.
(Ⅱ)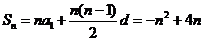
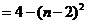 .
.
所以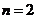 时,
时, 取到最大值
取到最大值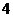 .
.
1.(安徽卷理21)设数列 满足
满足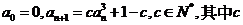 为实数
为实数
(Ⅰ)证明: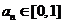 对任意
对任意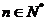 成立的充分必要条件是
成立的充分必要条件是 ;
;
(Ⅱ)设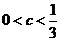 ,证明:
,证明: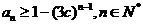 ;
;
(Ⅲ)设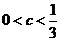 ,证明:
,证明:
解 (1) 必要性 : ,
,
又 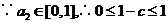 ,即
,即
充分性 :设 ,对
,对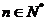 用数学归纳法证明
用数学归纳法证明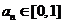
当 时,
时,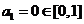 .假设
.假设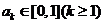
则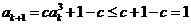 ,且
,且
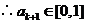 ,由数学归纳法知
,由数学归纳法知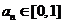 对所有
对所有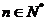 成立
成立
(2) 设 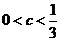 ,当
,当 时,
时, ,结论成立
,结论成立
当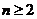 时,
时,

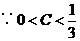 ,由(1)知
,由(1)知 ,所以
,所以 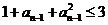 且
且 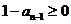

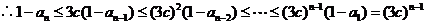
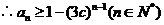
(3) 设 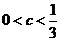 ,当
,当 时,
时,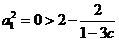 ,结论成立
,结论成立
当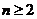 时,由(2)知
时,由(2)知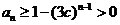
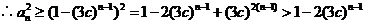
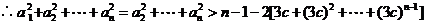
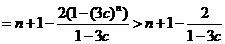
2.(安徽卷文21)设数列 满足
满足 其中
其中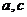 为实数,且
为实数,且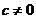
(Ⅰ)求数列 的通项公式
的通项公式
(Ⅱ)设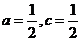 ,
,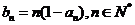 ,求数列
,求数列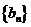 的前
的前 项和
项和 ;
;
(Ⅲ)若 对任意
对任意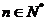 成立,证明
成立,证明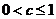
解 (1) 方法一: 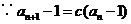
 当
当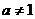 时,
时,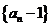 是首项为
是首项为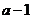 ,公比为
,公比为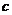 的等比数列。
的等比数列。
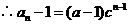 ,即
,即 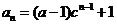 。当
。当 时,
时,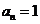 仍满足上式。
仍满足上式。
 数列
数列 的通项公式为
的通项公式为 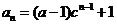
 。
。
方法二 由题设得:当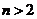 时,
时,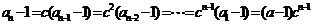

 时,
时,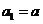 也满足上式。
也满足上式。
 数列
数列 的通项公式为
的通项公式为 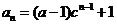
 。
。
(2) 由(1)得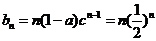
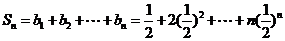
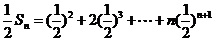

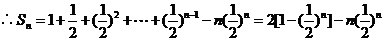

(3) 由(1)知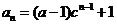
若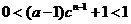 ,则
,则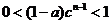
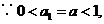
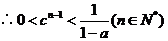
由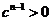 对任意
对任意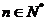 成立,知
成立,知 。下面证
。下面证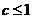 ,用反证法
,用反证法
方法一:假设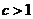 ,由函数
,由函数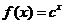 的函数图象知,当
的函数图象知,当 趋于无穷大时,
趋于无穷大时,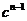 趋于无穷大
趋于无穷大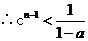 不能对
不能对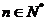 恒成立,导致矛盾。
恒成立,导致矛盾。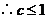 。
。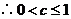
方法二:假设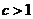 ,
,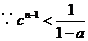 ,
,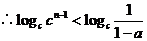
即 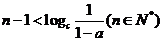 恒成立 (*)
恒成立 (*)
 为常数,
为常数, (*)式对
(*)式对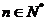 不能恒成立,导致矛盾,
不能恒成立,导致矛盾,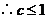
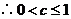

3.(北京卷理20)对于每项均是正整数的数列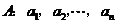 ,定义变换
,定义变换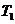 ,
,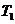 将数列
将数列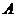 变换成数列
变换成数列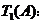
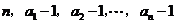 .对于每项均是非负整数的数列
.对于每项均是非负整数的数列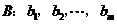 ,定义变换
,定义变换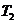 ,
,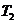 将数列
将数列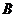 各项从大到小排列,然后去掉所有为零的项,得到数列
各项从大到小排列,然后去掉所有为零的项,得到数列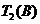 ;又定义
;又定义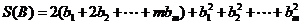 .设
.设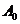 是每项均为正整数的有穷数列,令
是每项均为正整数的有穷数列,令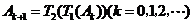 .
.
(Ⅰ)如果数列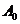 为5,3,2,写出数列
为5,3,2,写出数列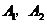 ;
;
(Ⅱ)对于每项均是正整数的有穷数列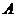 ,证明
,证明 ;
;
(Ⅲ)证明:对于任意给定的每项均为正整数的有穷数列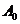 ,存在正整数
,存在正整数 ,当
,当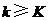 时,
时, .
.
解析:(Ⅰ)解: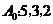 ,
,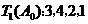 ,
,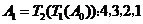 ;
;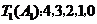 ,
,
 .
.
(Ⅱ)证明:设每项均是正整数的有穷数列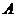 为
为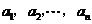 ,
,
则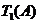 为
为 ,
, ,
,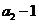 ,
, ,
,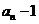 ,
,
从而

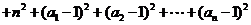 .
.
又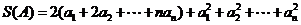 ,
,
所以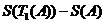

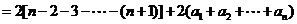


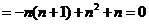 ,
,
故 .
.
(Ⅲ)证明:设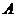 是每项均为非负整数的数列
是每项均为非负整数的数列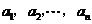 .
.
当存在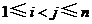 ,使得
,使得 时,交换数列
时,交换数列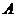 的第
的第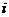 项与第
项与第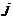 项得到数列
项得到数列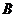 ,
,
则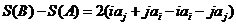
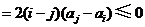 .
.
当存在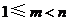 ,使得
,使得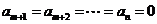 时,若记数列
时,若记数列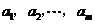 为
为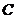 ,
,
则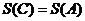 .
.
所以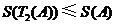 .
.
从而对于任意给定的数列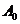 ,由
,由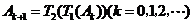

可知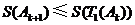 .
.
又由(Ⅱ)可知 ,所以
,所以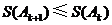 .
.
即对于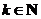 ,要么有
,要么有 ,要么有
,要么有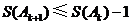 .
.
因为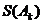 是大于2的整数,所以经过有限步后,必有
是大于2的整数,所以经过有限步后,必有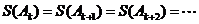 .
.
即存在正整数 ,当
,当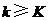 时,
时,

4.(北京卷文20)数列 满足
满足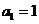 ,
,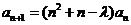 (
(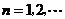 ),
),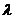 是常数.
是常数.
(Ⅰ)当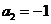 时,求
时,求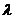 及
及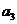 的值;
的值;
(Ⅱ)数列 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
(Ⅲ)求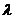 的取值范围,使得存在正整数
的取值范围,使得存在正整数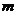 ,当
,当 时总有
时总有 .
.
解:(Ⅰ)由于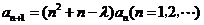 ,且
,且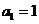 .
.
所以当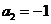 时,得
时,得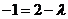 ,故
,故 .
.
从而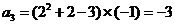 .
.
(Ⅱ)数列 不可能为等差数列,证明如下:由
不可能为等差数列,证明如下:由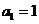 ,
,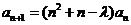

得 ,
,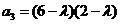 ,
,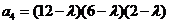 .
.
若存在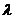 ,使
,使 为等差数列,则
为等差数列,则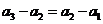 ,即
,即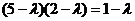 ,
,
解得 .于是
.于是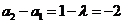 ,
,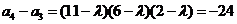 .
.
这与 为等差数列矛盾.所以,对任意
为等差数列矛盾.所以,对任意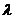 ,
, 都不可能是等差数列.
都不可能是等差数列.
(Ⅲ)记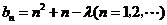 ,根据题意可知,
,根据题意可知,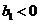 且
且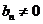 ,即
,即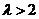

且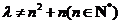 ,这时总存在
,这时总存在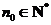 ,满足:当
,满足:当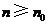 时,
时, ;
;
当 时,
时,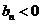 .所以由
.所以由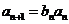 及
及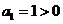 可知,若
可知,若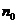 为偶数,
为偶数,
则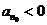 ,从而当
,从而当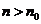 时,
时, ;若
;若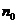 为奇数,则
为奇数,则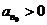 ,
,
从而当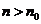 时
时 .因此“存在
.因此“存在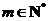 ,当
,当 时总有
时总有 ”
”
的充分必要条件是: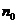 为偶数,
为偶数,
记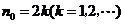 ,则
,则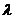 满足
满足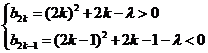 .
.
故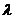 的取值范围是
的取值范围是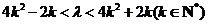 .
.
5.(福建卷理19)已知函数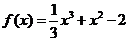 .
.
(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点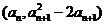 (n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(Ⅱ)求函数f(x)在区间(a-1,a)内的极值.
解:(Ⅰ)证明: 因为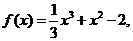 所以
所以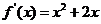 ,
,
由点 在函数
在函数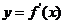 的图象上,
的图象上,

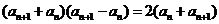 , 又
, 又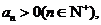

所以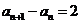 ,
, 是
是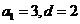 的等差数列
的等差数列
所以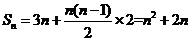 ,又因为
,又因为 ,所以
,所以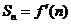 ,
,
故点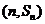 也在函数
也在函数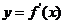 的图象上.
的图象上.
(Ⅱ)解: ,令
,令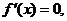 得
得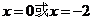 .
.
当x变化时,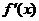 ﹑
﹑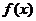 的变化情况如下表:
的变化情况如下表:
|
x |
(-∞,-2) |
-2 |
(-2,0) |
0 |
(0,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
注意到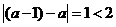 ,从而
,从而
①当 ,此时
,此时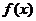 无极小值;
无极小值;
②当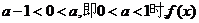 的极小值为
的极小值为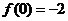 ,此时
,此时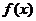 无极大值;
无极大值;
③当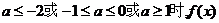 既无极大值又无极小值.
既无极大值又无极小值.
6.(广东卷理21)设 为实数,
为实数,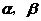 是方程
是方程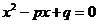 的两个实根,数列
的两个实根,数列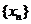 满足
满足 ,
,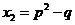 ,
,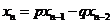 (
(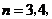 …).
…).
(1)证明: ,
,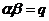 ;
;
(2)求数列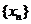 的通项公式;
的通项公式;
(3)若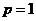 ,
,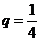 ,求
,求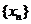 的前
的前 项和
项和 .
.
[解析](1)由求根公式,不妨设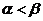 ,得
,得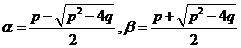

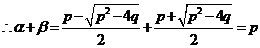 ,
,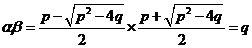

(2)设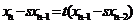 ,则
,则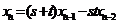 ,由
,由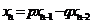 得
得 ,
,
消去 ,得
,得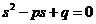 ,
,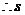 是方程
是方程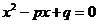 的根,由题意可知,
的根,由题意可知,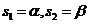

①当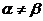 时,此时方程组
时,此时方程组 的解记为
的解记为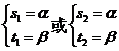

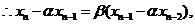
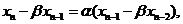

即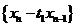 、
、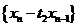 分别是公比为
分别是公比为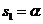 、
、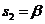 的等比数列,
的等比数列,
由等比数列性质可得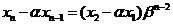 ,
,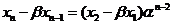 ,
,
两式相减,得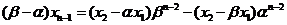

 ,
,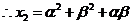 ,
,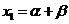

 ,
,

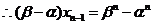 ,即
,即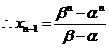 ,
,

②当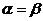 时,即方程
时,即方程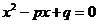 有重根,
有重根,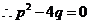 ,
,
即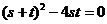 ,得
,得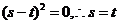 ,不妨设
,不妨设 ,由①可知
,由①可知
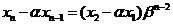 ,
,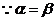 ,
,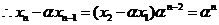

即 ,等式两边同时除以
,等式两边同时除以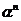 ,得
,得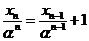 ,即
,即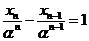

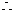 数列
数列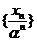 是以1为公差的等差数列,
是以1为公差的等差数列, ,
,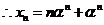

综上所述,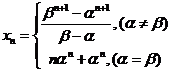
(3)把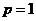 ,
,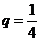 代入
代入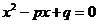 ,得
,得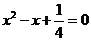 ,解得
,解得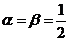
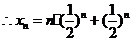
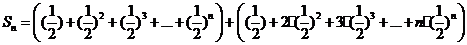
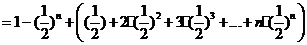

7.(广东卷文21)设数列 满足
满足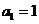 ,
,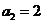 ,
,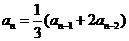
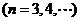 。数列
。数列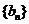 满足
满足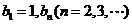 是非零整数,且对任意的正整数
是非零整数,且对任意的正整数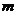 和自然数
和自然数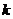 ,都有
,都有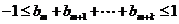 。
。
(1)求数列 和
和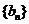 的通项公式;
的通项公式;
(2)记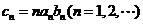 ,求数列
,求数列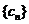 的前
的前 项和
项和 。
。
[解析](1)由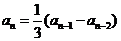 得
得 
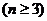
又 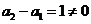 ,
, 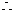 数列
数列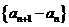 是首项为1公比为
是首项为1公比为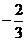 的等比数列,
的等比数列,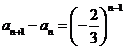
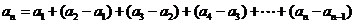

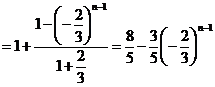 ,
,
 由
由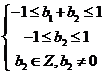 得
得  ,由
,由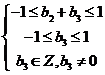 得
得 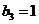 ,…
,…
同理可得当n为偶数时,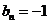 ;当n为奇数时,
;当n为奇数时, ;因此
;因此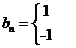
 (2)
(2)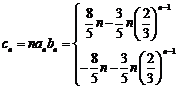
试题详情
(二)填空题(共2题)
1.(北京卷理14)某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第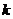 棵树种植在点
棵树种植在点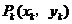 处,其中
处,其中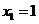 ,
, ,当
,当 时,
时,
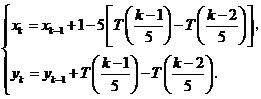
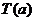 表示非负实数
表示非负实数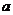 的整数部分,例如
的整数部分,例如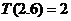 ,
,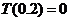 .
.
按此方案,第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 .
[标准答案]: (1,2) (3, 402)
[试题分析]: T 组成的数列为1,0,0,0,0,1, 0,0,0,0,1, 0,0,0,0,1……(k=1,2,3,4……)。一一带入计算得:数列
组成的数列为1,0,0,0,0,1, 0,0,0,0,1, 0,0,0,0,1……(k=1,2,3,4……)。一一带入计算得:数列 为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5……;数列
为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5……;数列 为1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4…….因此,第6棵树种在 (1,2),第2008棵树种在(3, 402)。
为1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4…….因此,第6棵树种在 (1,2),第2008棵树种在(3, 402)。
[高考考点]: 数列的通项
[易错提醒]: 前几项的规律找错
[备考提示]: 创新题大家都没有遇到过,仔细认真地从前几项(特殊处、简单处)体会题意,从而找到解题方法。
2.(四川卷文16)设数列 中,
中,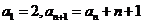 ,则通项
,则通项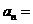 ___________。
___________。
[解]:∵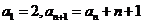 ∴
∴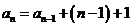 ,
, ,
,
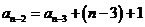 ,
,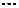 ,
,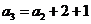 ,
,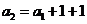 ,
,
将以上各式相加得: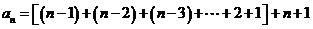
 故应填
故应填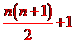 ;
;
1.(安徽卷文15)在数列 在中,
在中,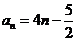 ,
,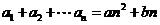 ,
,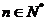 ,其中
,其中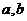 为常数,则
为常数,则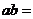
解:∵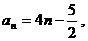 ∴
∴ 从而
从而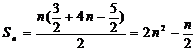 。
。
∴a=2,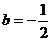 ,则
,则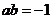
2.(海南宁夏卷文13)已知{an}为等差数列,a3 + a8 = 22,a6 = 7,则a5 = ____________
[标准答案]:15
[试题解析]:由于 为等差数列,故
为等差数列,故 ∴
∴
[易错点]:对有关性质掌握不到位而出错。
[备考提示]:等差数列及等比数列“足数和定理”是数列中的重点内容,要予以重点掌握并灵活应用。
3.(湖北卷理14)已知函数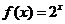 ,等差数列
,等差数列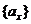 的公差为
的公差为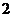 .若
.若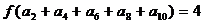 ,则
,则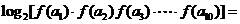 .
.
解:依题意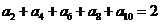 ,所以
,所以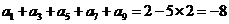
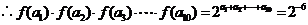
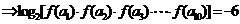
4.(四川卷理16)设等差数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则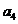 的最大值为___________。
的最大值为___________。
[解]:∵等差数列 的前
的前 项和为
项和为 ,且
,且
∴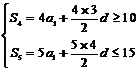 即
即 ∴
∴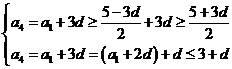
∴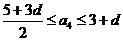 ,
,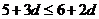 ,
, 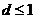
∴ 故
故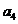 的最大值为
的最大值为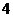 ,应填
,应填
[点评]:此题重点考察等差数列的通项公式,前 项和公式,以及不等式的变形求范围;
项和公式,以及不等式的变形求范围;
[突破]:利用等差数列的前 项和公式变形不等式,利用消元思想确定
项和公式变形不等式,利用消元思想确定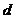 或
或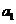 的范围解答本题的关键;
的范围解答本题的关键;
5.(重庆卷理14)设Sn=是等差数列{an}的前n项和,a12=-8,S9=-9,则S16= .
解: 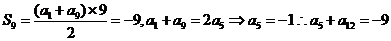 ,
,
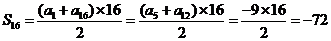
6.(上海春卷5)已知数列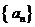 是公差不为零的等差数列,
是公差不为零的等差数列,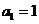 .
若
.
若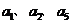 成等比数列,则
成等比数列,则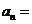 .
.
解析:原设等差数列的公差为d,由a22=a1a5得(1+d)2=1(1+4d)即d2-2d=0解得d=0(舍)或d=2,于是an=1+(n-1)2=2n-1.
7.(四川延考理14文15)设等差数列 的前
的前 项和为
项和为 ,且
,且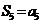 。若
。若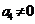 ,则
,则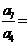 。
。
解: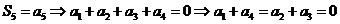 ,取特殊值
,取特殊值
令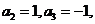
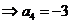
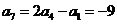 ,所以
,所以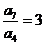
(一)选择题
1.(北京卷理6).已知数列 对任意的
对任意的 满足
满足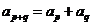 ,且
,且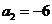 ,那么
,那么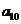 等于( )
等于( )
A.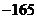 B.
B.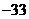 C.
C. D.
D.
[标准答案]: C
[试题分析]: 由已知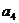 =
=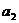 +
+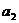 = -12,
= -12,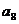 =
=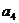 +
+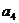 =-24,
=-24,
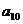 =
=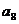 +
+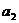 = -30
= -30
[高考考点]: 数列
[易错提醒]: 特殊性的运用
[备考提示]: 加强从一般性中发现特殊性的训练。
2.(江西卷理5文5)在数列 中,
中,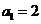 ,
, 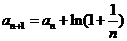 ,则
,则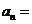
A.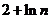 B.
B.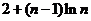 C.
C. D.
D.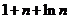
解析: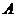 .
. 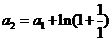 ,
,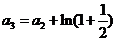 ,…,
,…,

1.(北京卷文7)已知等差数列 中,
中,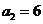 ,
,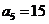 ,若
,若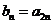 ,则数列
,则数列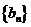 的前5项和等于( )
的前5项和等于( )
A.30 B.45 C.90 D.186
[解析]由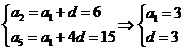 ,
, 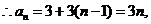
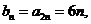
所以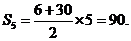 [答案] C
[答案] C
2.(福建卷文3)设|an|是等左数列,若a2=3,a1=13,则数列{an}前8项的和为
A.128 B.80 C.64 D.56
解:因为 是等差数列,
是等差数列,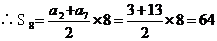
3.(广东卷理2)记等差数列 的前
的前 项和为
项和为 ,若
,若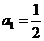 ,
,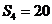 ,则
,则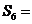 ( )
( )
A.16 B.24 C.36 D.48
[解析]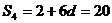 ,
,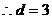 ,故
,故
4.(广东卷文4)记等差数列的前 项和为
项和为 ,若
,若 ,则该数列的公差
,则该数列的公差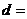 ( )
( )
A、2 B、3 C、6 D、7
[解析]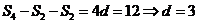 ,选B.
,选B.
5.(全国Ⅰ卷理5)已知等差数列 满足
满足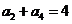 ,
,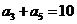 ,则它的前10项的和
,则它的前10项的和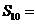 ( )
( )
A.138 B.135 C.95 D.23
[解析]C. 由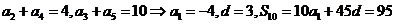 ;
;
6.(陕西卷理4文4)已知 是等差数列,
是等差数列,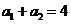 ,
,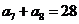 ,则该数列前10项和
,则该数列前10项和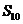 等于( )
等于( )
A.64 B.100 C.110 D.120
解:设公差为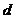 ,则由已知得
,则由已知得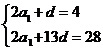
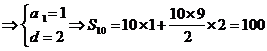
7.(天津卷文4)若等差数列 的前5项和
的前5项和 ,且
,且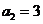 ,则
,则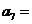 ( )
( )
A.12 B.13 C.14 D.15
解析: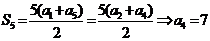 ,所以
,所以 ,选B.
,选B.
8.(重庆卷文1)已知{an}为等差数列,a2+a8=12,则a5等于
(A)4 (B)5 (C)6 (D)7
[解析]本小题主要考查等差数列的性质。由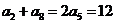 得:
得: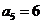 ,故选C。
,故选C。
1.(福建理3)设{an}是公比为正数的等比数列,若n1=7,a5=16,则数列{an}前7项的和为( )
A.63 B.64 C.127 D.128
解:由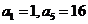 及{an}是公比为正数得公比
及{an}是公比为正数得公比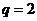 ,所以
,所以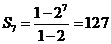
2.(海南宁夏卷理4文8)设等比数列 的公比
的公比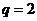 ,前n项和为
,前n项和为 ,则
,则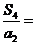 ( )
( )
A. 2 B. 4 C. 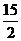 D.
D. 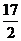
解: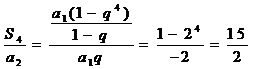
3.(全国Ⅰ卷文7)已知等比数列 满足
满足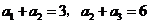 ,则
,则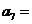 ( )
( )
A.64 B.81 C.128 D.243
 .(四川卷理7)已知等比数列
.(四川卷理7)已知等比数列 中
中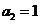 ,则其前3项的和
,则其前3项的和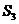 的取值范围是( )
的取值范围是( )
(A)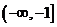 (B)
(B)
(C) (D)
(D)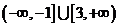
[解1]:∵等比数列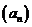 中
中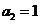 ∴当公比为1时,
∴当公比为1时, ,
,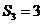 ;
;
当公比为 时,
时,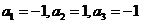 ,
,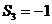 从而淘汰(A)(B)(C)故选D;
从而淘汰(A)(B)(C)故选D;
[解2]:∵等比数列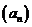 中
中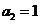 ∴
∴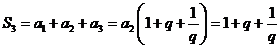
∴当公比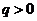 时,
时,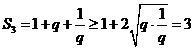 ; 当公比
; 当公比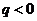 时,
时,
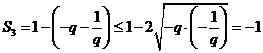 ∴
∴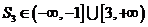 故选D;
故选D;
[考点]:此题重点考察等比数列前 项和的意义,等比数列的通项公式,以及均值不等式的应用;[突破]:特殊数列入手淘汰;重视等比数列的通项公式,前
项和的意义,等比数列的通项公式,以及均值不等式的应用;[突破]:特殊数列入手淘汰;重视等比数列的通项公式,前 项和,以及均值不等式的应用,特别是均值不等式使用的条件;
项和,以及均值不等式的应用,特别是均值不等式使用的条件;
5.(浙江卷理6)已知 是等比数列,
是等比数列,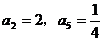 ,则
,则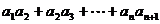 =
=
(A)16( )
(B)16(
)
(B)16(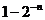 ) (C)
) (C)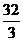 (
( )(D)
)(D)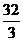 (
(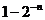 )
)
解析:本小题主要考查等比数列通项的性质。由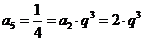 ,解得
,解得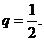
数列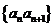 仍是等比数列:其首项是
仍是等比数列:其首项是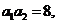 公比为
公比为 所以,
所以, 
6.(浙江卷文4)已知 是等比数列,
是等比数列,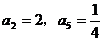 ,则公比
,则公比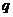 =
=
(A)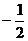 (B)
(B)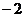 (C)2
(D)
(C)2
(D)
答案:D
解析:本小题主要考查等比数列通项的性质。由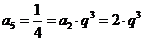 ,解得
,解得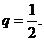
1.(2009年广东卷文)(本小题满分14分)已知点(1,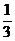 )是函数
)是函数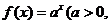 且
且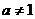 )的图象上一点,等比数列
)的图象上一点,等比数列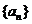 的前
的前 项和为
项和为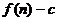 ,数列
,数列
 的首项为
的首项为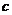 ,且前
,且前 项和
项和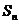 满足
满足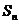 -
-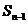 =
=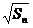 +
+ (
(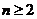 ).(1)求数列
).(1)求数列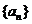 和
和 的通项公式;(2)若数列{
的通项公式;(2)若数列{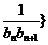 前
前 项和为
项和为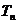 ,问
,问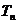 >
> 的最小正整数
的最小正整数 是多少?
是多少? 

[解析](1) ,
,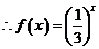
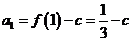 ,
,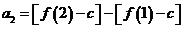
 ,
,
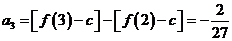 .
.
又数列 成等比数列,
成等比数列, ,所以
,所以 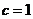 ;
;
又公比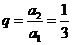 ,所以
,所以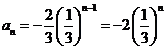
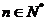 ;
;


又 ,
,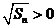 ,
, 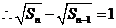 ;
;
数列 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列, ,
, 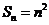
当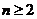 ,
, 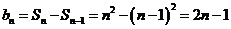 ;
; (
(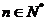 );
);
(2)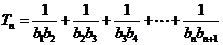
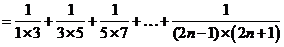
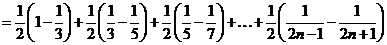
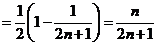 ;
;
由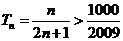 得
得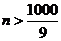 ,满足
,满足 的最小正整数为112.
的最小正整数为112.
2.(2009全国卷Ⅰ理)(本小题满分12分)在数列 中,
中,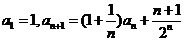 (I)设
(I)设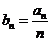 ,求数列
,求数列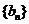 的通项公式 (II)求数列
的通项公式 (II)求数列 的前
的前 项和
项和
分析:(I)由已知有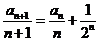

利用累差迭加即可求出数列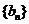 的通项公式:
的通项公式: 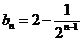 (
(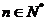 )
)
(II)由(I)知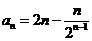 ,
,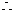
 =
=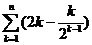
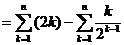
而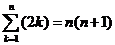 ,又
,又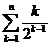 是一个典型的错位相减法模型,
是一个典型的错位相减法模型,
易得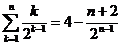
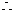
 =
=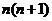
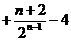
评析:09年高考理科数学全国(一)试题将数列题前置,考查构造新数列和利用错位相减法求前n项和,一改往年的将数列结合不等式放缩法问题作为押轴题的命题模式。具有让考生和一线教师重视教材和基础知识、基本方法基本技能,重视两纲的导向作用。也可看出命题人在有意识降低难度和求变的良苦用心。
3.(2009浙江文)(本题满分14分)设 为数列
为数列 的前
的前 项和,
项和, ,
,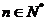 ,其中
,其中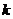 是常数.(I) 求
是常数.(I) 求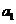 及
及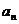 ;(II)若对于任意的
;(II)若对于任意的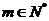 ,
,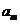 ,
,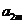 ,
, 成等比数列,求
成等比数列,求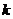 的值.
的值.
解析:(Ⅰ)当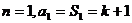 ,
,
 (
(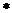 )
)
经验,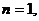 (
(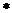 )式成立,
)式成立,
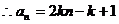
(Ⅱ)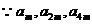 成等比数列,
成等比数列, ,
,
即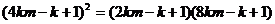 ,整理得:
,整理得: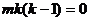 ,
,
对任意的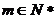 成立,
成立, 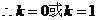
4.(2009北京文)(本小题共13分)设数列 的通项公式为
的通项公式为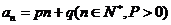 . 数列
. 数列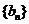 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值.(Ⅰ)若
成立的所有n中的最小值.(Ⅰ)若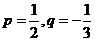 ,求
,求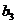 ;(Ⅱ)若
;(Ⅱ)若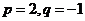 ,求数列
,求数列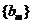 的前2m项和公式;(Ⅲ)是否存在p和q,使得
的前2m项和公式;(Ⅲ)是否存在p和q,使得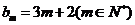 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
[解析]本题主要考查数列的概念、数列的基本性质,考查运算能力、推理论证能力、
分类讨论等数学思想方法.本题是数列与不等式综合的较难层次题.
(Ⅰ)由题意,得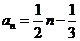 ,解
,解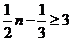 ,得
,得 .
. 

∴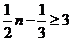 成立的所有n中的最小整数为7,即
成立的所有n中的最小整数为7,即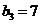 .
.
(Ⅱ)由题意,得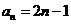 ,对于正整数,由
,对于正整数,由 ,得
,得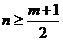 .
.
根据 的定义可知当
的定义可知当 时,
时,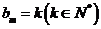 ;当
;当 时,
时, .
.
∴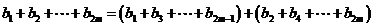
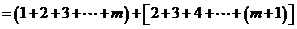
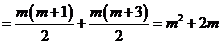 .
.
(Ⅲ)假设存在p和q满足条件,由不等式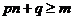 及
及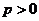 得
得 .
.
∵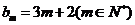 ,根据
,根据 的定义可知,对于任意的正整数m 都有
的定义可知,对于任意的正整数m 都有
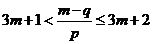 ,即
,即 对任意的正整数m都成立.
对任意的正整数m都成立.
当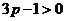 (或
(或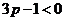 )时,得
)时,得 (或
(或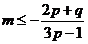 ), 这与上述结论矛盾!
), 这与上述结论矛盾!
当 ,即
,即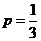 时,得
时,得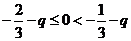 ,解得
,解得 .
.
∴ 存在p和q,使得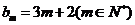 ;p和q的取值范围分别是
;p和q的取值范围分别是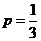 ,
, .
. 
 5.(2009北京理)(本小题共13分)
5.(2009北京理)(本小题共13分)
已知数集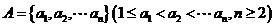 具有性质
具有性质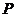 ;对任意的
;对任意的
 ,
,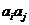 与
与 两数中至少有一个属于
两数中至少有一个属于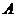 .
.
(Ⅰ)分别判断数集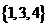 与
与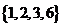 是否具有性质
是否具有性质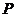 ,并说明理由;
,并说明理由;
(Ⅱ)证明: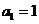 ,且
,且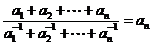 ;
;
(Ⅲ)证明:当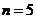 时,
时,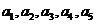 成等比数列.
成等比数列.
[解析]本题主要考查集合、等比数列的性质,考查运算能力、推理论证能力、分
分类讨论等数学思想方法.本题是数列与不等式的综合题,属于较难层次题.
(Ⅰ)由于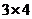 与
与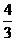 均不属于数集
均不属于数集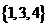 ,∴该数集不具有性质P.
,∴该数集不具有性质P.
由于 都属于数集
都属于数集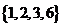 , ∴该数集具有性质P.
, ∴该数集具有性质P.
(Ⅱ)∵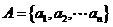 具有性质P,∴
具有性质P,∴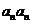 与
与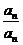 中至少有一个属于A,
中至少有一个属于A,
由于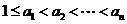 ,∴
,∴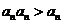 ,故
,故 .
. 

从而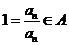 ,∴
,∴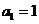 .
.
∵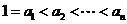 , ∴
, ∴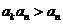 ,故
,故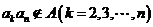 .
.
由A具有性质P可知 .
.
又∵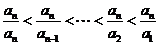 ,
,
∴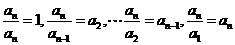 ,
,
从而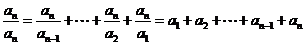 ,
,
∴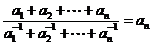 .
. 

(Ⅲ)由(Ⅱ)知,当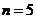 时,有
时,有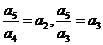 ,即
,即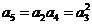 ,
,
∵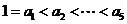 ,∴
,∴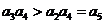 ,∴
,∴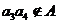 ,
,
由A具有性质P可知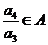 .
.
 ,得
,得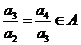 ,且
,且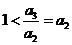 ,∴
,∴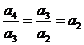 ,
,
∴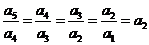 ,即
,即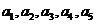 是首项为1,公比为
是首项为1,公比为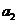 成等比数列..k.s.5.
成等比数列..k.s.5.
6.(2009江苏卷)(本小题满分14分)设 是公差不为零的等差数列,
是公差不为零的等差数列, 为其前
为其前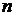 项和,满足
项和,满足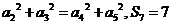 。(1)求数列
。(1)求数列 的通项公式及前
的通项公式及前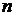 项和
项和 ;(2)试求所有的正整数
;(2)试求所有的正整数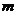 ,使得
,使得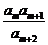 为数列
为数列 中的项。
中的项。 
[解析] 本小题主要考查等差数列的通项、求和的有关知识,考查运算和求解的能力。满分14分。
(1)设公差为 ,则
,则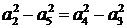 ,由性质得
,由性质得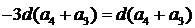 ,因为
,因为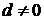 ,所以
,所以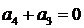 ,即
,即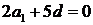 ,又由
,又由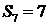 得
得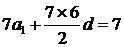 ,解得
,解得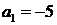 ,
, ,
,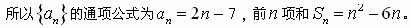
(2) (方法一)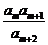 =
=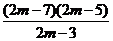 ,设
,设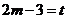 ,
, 
则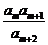 =
=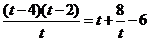 , 所以
, 所以 为8的约数
为8的约数

(方法二)因为 为数列
为数列 中的项,
中的项,
故 为整数,又由(1)知:
为整数,又由(1)知: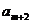 为奇数,所以
为奇数,所以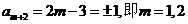
经检验,符合题意的正整数只有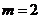 。
。 

7.(2009山东卷理)等比数列{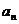 }的前n项和为
}的前n项和为 ,
已知对任意的
,
已知对任意的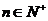 ,点
,点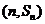 ,均在函数
,均在函数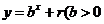 且
且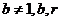 均为常数)的图像上.(1)求r的值;(11)当b=2时,记
均为常数)的图像上.(1)求r的值;(11)当b=2时,记 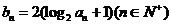 证明:对任意的
证明:对任意的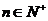 ,不等式
,不等式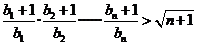 成立
成立
解:因为对任意的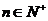 ,点
,点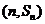 ,均在函数
,均在函数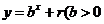 且
且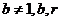 均为常数的图像上.所以得
均为常数的图像上.所以得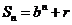 ,当
,当 时,
时,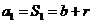 ,当
,当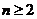 时,
时,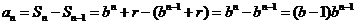 ,又因为{
,又因为{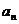 }为等比数列,所以
}为等比数列,所以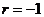 ,公比为
,公比为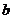 ,
,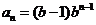
(2)当b=2时,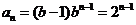 ,
, 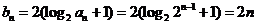
则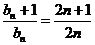 ,所以
,所以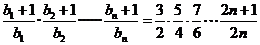


下面用数学归纳法证明不等式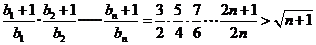 成立.
成立.
① 当 时,左边=
时,左边=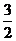 ,右边=
,右边=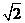 ,因为
,因为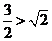 ,所以不等式成立.
,所以不等式成立.
② 假设当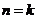 时不等式成立,即
时不等式成立,即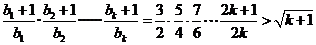 成立.则当
成立.则当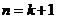 时,左边=
时,左边=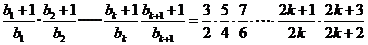
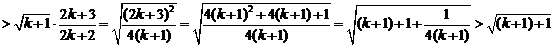
所以当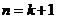 时,不等式也成立.
时,不等式也成立. 

由①、②可得不等式恒成立.
[命题立意]:本题主要考查了等比数列的定义,通项公式,以及已知 求
求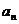 的基本题型,并运用数学归纳法证明与自然数有关的命题,以及放缩法证明不等式.
的基本题型,并运用数学归纳法证明与自然数有关的命题,以及放缩法证明不等式.
8.(2009山东卷文)等比数列{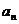 }的前n项和为
}的前n项和为 ,
已知对任意的
,
已知对任意的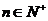 ,点
,点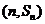 ,均在函数
,均在函数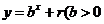 且
且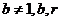 均为常数)的图像上.
均为常数)的图像上. 
 (1)求r的值;(11)当b=2时,记
(1)求r的值;(11)当b=2时,记  求数列
求数列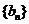 的前
的前 项和
项和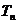
解:因为对任意的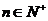 ,点
,点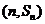 ,均在函数
,均在函数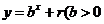 且
且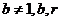 均为常数)的图像上.所以得
均为常数)的图像上.所以得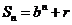 ,当
,当 时,
时,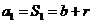 ,
,


当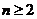 时,
时,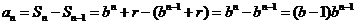 ,
,
又因为{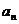 }为等比数列, 所以
}为等比数列, 所以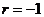 , 公比为
, 公比为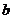 , 所以
, 所以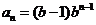
(2)当b=2时,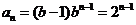 ,
, 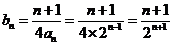
则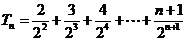
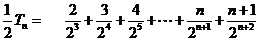


相减,得
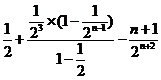
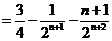 所以
所以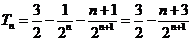
[命题立意]:本题主要考查了等比数列的定义,通项公式,以及已知 求
求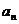 的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前
的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前 项和
项和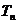 .
.
9.(2009全国卷Ⅱ文)(本小题满分10分)已知等差数列{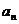 }中,
}中,
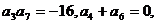 求{
求{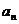 }前n项和
}前n项和
解析:本题考查等差数列的基本性质及求和公式运用能力,利用方程的思想可求解。
解:设 的公差为
的公差为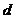 ,则
,则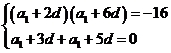 即
即
解得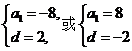 因此
因此
10.(2009广东卷理)(本小题满分14分)w.w.w已知曲线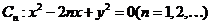 .从点
.从点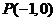 向曲线
向曲线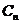 引斜率为
引斜率为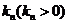 的切线
的切线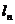 ,切点为
,切点为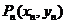 .(1)求数列
.(1)求数列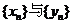 的通项公式;(2)证明:
的通项公式;(2)证明: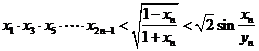 .
.
解:(1)设直线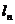 :
: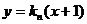 ,联立
,联立 得
得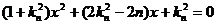 ,则
,则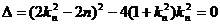 ,∴
,∴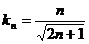 (
(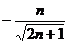 舍去)
舍去) 

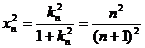 ,即
,即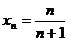 ,∴
,∴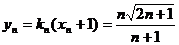
(2)证明:∵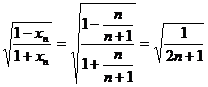



∴
由于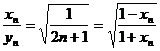 ,可令函数
,可令函数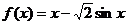 ,则
,则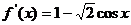 ,令
,令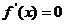 ,得
,得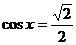 ,给定区间
,给定区间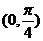 ,则有
,则有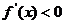 ,则函数
,则函数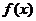 在
在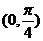 上单调递减,∴
上单调递减,∴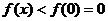 ,即
,即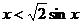 在
在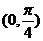 恒成立,又
恒成立,又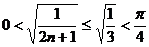 ,
,
则有 ,即
,即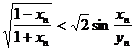 .
.




11.(2009安徽卷理)(本小题满分13分)首项为正数的数列 满足
满足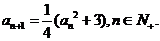

 (I)证明:若
(I)证明:若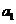 为奇数,则对一切
为奇数,则对一切 都是奇数;
都是奇数;
(II)若对一切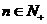 都有
都有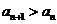 ,求
,求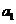 的取值范围.
的取值范围.
解:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知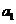 是奇数,假设
是奇数,假设 是奇数,其中
是奇数,其中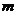 为正整数,
为正整数,
则由递推关系得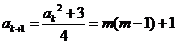 是奇数。
是奇数。 
 根据数学归纳法,对任何
根据数学归纳法,对任何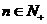 ,
,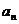 都是奇数。
都是奇数。
(II)(方法一)由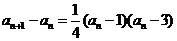 知,
知,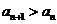 当且仅当
当且仅当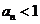 或
或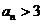 。
。
另一方面,若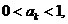 则
则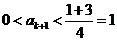 ;若
;若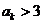 ,则
,则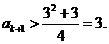
根据数学归纳法,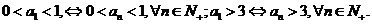
综合所述,对一切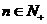 都有
都有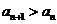 的充要条件是
的充要条件是 或
或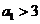 。
。
(方法二)由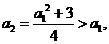 得
得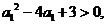 于是
于是 或
或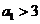 。
。
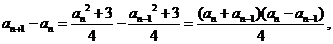


因为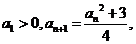 所以所有的
所以所有的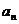 均大于0,因此
均大于0,因此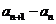 与
与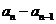 同号。
同号。
根据数学归纳法,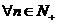 ,
,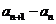 与
与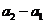 同号。
同号。 

因此,对一切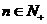 都有
都有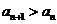 的充要条件是
的充要条件是 或
或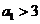 。
。
12.(2009安徽卷文)(本小题满分12分)已知数列{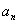 } 的前n项和
} 的前n项和 ,数列{
,数列{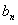 }的前n项和
}的前n项和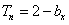 (Ⅰ)求数列{
(Ⅰ)求数列{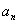 }与{
}与{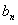 }的通项公式;(Ⅱ)设
}的通项公式;(Ⅱ)设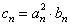 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时,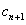 <
<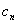


[思路]由 可求出
可求出 ,这是数列中求通项的常用方法之一,在求出
,这是数列中求通项的常用方法之一,在求出 后,进而得到
后,进而得到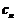 ,接下来用作差法来比较大小,这也是一常用方法。
,接下来用作差法来比较大小,这也是一常用方法。
[解析](1)由于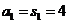
当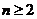 时,
时, 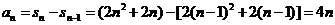
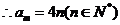
又当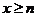 时
时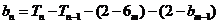
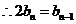
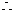 数列
数列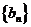 项与等比数列,其首项为1,公比为
项与等比数列,其首项为1,公比为



(2)由(1)知
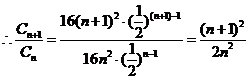
由 即
即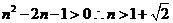 即
即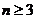
又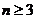 时
时 成立,即
成立,即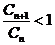 由于
由于 恒成立.
恒成立.


因此,当且仅当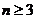 时,
时, 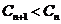
13.(2009江西卷文)数列 的通项
的通项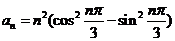 ,其前n项和为
,其前n项和为 . (1) 求
. (1) 求 ; (2)
; (2)  求数列{
求数列{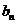 }的前n项和
}的前n项和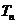 .
.
解: (1) 由于 ,故
,故
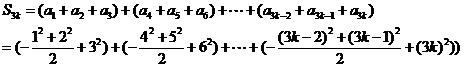
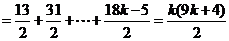 ,
,
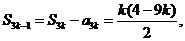
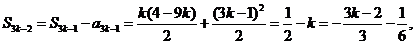
故 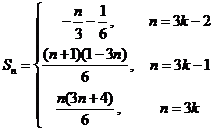 (
(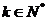 )
)
(2) 
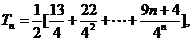
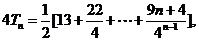
两式相减得
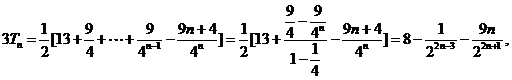
故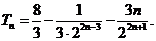
14.(2009江西卷理)各项均为正数的数列 ,
,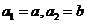 ,且对满足
,且对满足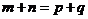 的正整数
的正整数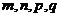 都有
都有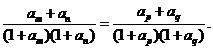 (1)当
(1)当 时,求通项
时,求通项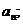 w.w.w
w.w.w 

(2)证明:对任意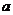 ,存在与
,存在与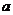 有关的常数
有关的常数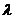 ,使得对于每个正整数
,使得对于每个正整数 ,都有
,都有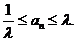
解:(1)由 得
得
试题详情
19.(2009重庆卷理)设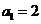 ,
,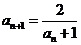 ,
,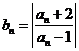 ,
,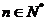 ,则数列
,则数列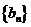 的通项公式
的通项公式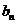 =
.[答案]:2n+1
=
.[答案]:2n+1
[解析]由条件得 且
且 所以数列
所以数列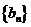 是首项为4,公比为2的等比数列,则
是首项为4,公比为2的等比数列,则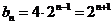
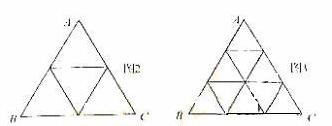
18.(2009湖南卷理)将正⊿ABC分割成
 (
( ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)=
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= 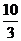 ,…,f(n)=
,…,f(n)= 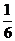 (n+1)(n+2)
(n+1)(n+2) 


[答案]:
[解析]当n=3时,如图所示分别设各顶点的数用小写字母表示,即由条件知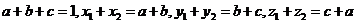
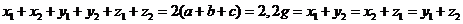
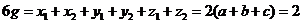


即
进一步可求得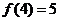 。由上知
。由上知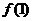 中有三个数,
中有三个数,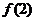 中
有6个数,
中
有6个数, 中共有10个数相加 ,
中共有10个数相加 , 中有15个数相加….,若
中有15个数相加….,若 中有
中有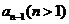 个数相加,可得
个数相加,可得 中有
中有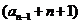 个数相加,且由
个数相加,且由
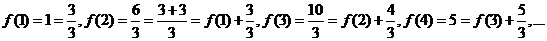
可得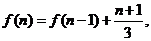 所以
所以
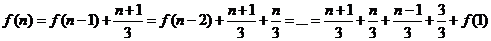
=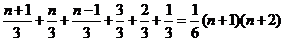
17.(2009宁夏海南卷文)等比数列{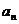 }的公比
}的公比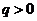 , 已知
, 已知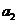 =1,
=1, ,则{
,则{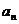 }的前4项和
}的前4项和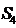 =
= 

[答案]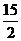
[解析]由 得:
得: ,即
,即 ,
,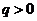 ,解得:q=2,又
,解得:q=2,又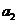 =1,所以,
=1,所以,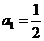 ,
,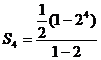 =
=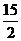 。
。
16.(2009陕西卷理)设等差数列 的前n项和为
的前n项和为 ,若
,若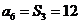 ,则
,则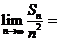 .
.
答案:1
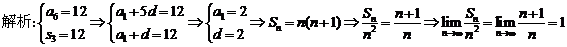
15.(2009陕西卷文)设等差数列 的前n项和为
的前n项和为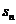 ,若
,若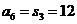 ,则
,则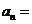 .
.


答案:2n
解析:由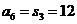 可得
可得 的公差d=2,首项
的公差d=2,首项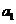 =2,故易得
=2,故易得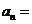 2n.
2n.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com