
2. 能用打点计时器或其他实验仪器得到相关的运动轨迹并能自主进行分析。
1. 认识自由落体运动,知道影响物体下落快慢的因素,理解自由落体运动是初速度为零的匀加速直线运动。
3.列车在恒定功率的机车牵引下,从车站出发行驶5min速度达到72km/h,这个过程中列车的加速度不断减小,那么这段时间内列车行驶的距离( )
A.小于3km B.等于3km
C.大于3km D.不能确定
答案:C
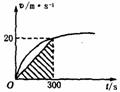 解析:72km/h=20m/s,5min=300s,如果列车做匀加速运动,它的速度图象为一条直线,它的位移大小就等于图中画阴影的三角形的“面积”,即位移是3km.而实际上,列车的加速度不断减小,图象的斜率不断减小,画出v-t图象如图所示,是一条曲线,图象下的“面积”等于列车的位移,它大于画阴影的三角形的“面积”,所以应选C.
解析:72km/h=20m/s,5min=300s,如果列车做匀加速运动,它的速度图象为一条直线,它的位移大小就等于图中画阴影的三角形的“面积”,即位移是3km.而实际上,列车的加速度不断减小,图象的斜率不断减小,画出v-t图象如图所示,是一条曲线,图象下的“面积”等于列车的位移,它大于画阴影的三角形的“面积”,所以应选C.
点评:这个题目如果用公式计算,高中阶段还不具备相应的数学知识。而用图象,却能形象、直观地把列车在不同过程中的位移表现出来.
新题解答
一个质点沿着x轴正方向运动,其位移一时间图象(s-t图)和加速度一时间图象(a-t图)分别如图1-11的甲、乙图所示.能正确反映质点速度随时间变化规律的图象,是图1-12中各v-t图中的哪一个?
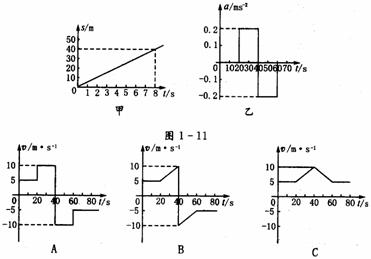
图1-12
解析:从甲图可看出质点开始做匀速直线运动,从乙图看出匀加速时间为20-40s,加速度大小0.2m/s 2,40-60s做匀减速直线运动,加速度为-0.2m/s2.
因此40-60s时间内质点做匀减速运动.故选C图.
2.某物体的运动图象如图.
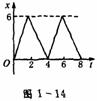 ①若x表示位移,则物体做( )
①若x表示位移,则物体做( )
A.往复运动
B.匀速直线运动
C.朝某一方向的直线运动
D.匀变速直线运动
②若x表示速度,则物体做( )
A.往复运动
B.匀速直线运动
C.朝某一方向的直线运动
D.匀变速直线运动
答案:①A②C
解析:①位移图线的斜率表示速度,图线的斜率在0-2s、4-6s为正,2-4s、6-8s为负,表示相应的速度一会为正,一会为负,故是往复运动.A正确.
②速度图线的斜率表示加速度,图线的斜率在0-2s、4-6s为正,2-4s、6-8s为负,表示相应的加速度一会为正,一会为负,但大小相等.而由图象可知速度均为正.C正确.
1.下面的s-t图象表示物体做怎样的运动( )

图1-13
解析:A图:物体做匀速直线运动,出发点不在位移的初位置.B图:物体做匀速直线运动,物体在计时后一段时间出发.C图:物体做匀速直线运动,但运动方向是指向位移的初位置.D图:物体先做匀速直线运动,停了一段时间,然后又匀速返回,而且返回时速度大些.E图:物体先做匀速直线运动,停了一段时间,然后继续以同样的速度大小匀速向前.
4.匀减速直线运动的图象
匀减速直线运动的图象是一条斜向下倾斜的直线.
速度图象的意义:
(1)能反映任一时刻的速度.
(2)图象的倾斜程度(斜率)反映速度变化的快慢,即加速度.
(3)图象与横轴t所围成的面积表示物体发生的位移.
[例2]一辆汽车沿着笔直的公路行驶,其速度图象如图1-10所示.
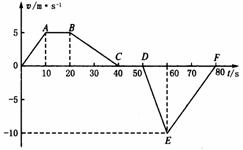
图1-10
(1)说明图中OA、AB、BC、CD、DE、EF各线段表示的是什么运动.
(2)根据图中折线和有关数据求出汽车在整个行驶过程中所通过的路程和位移.
思路:v-t图象反映了速度随时间变化的规律,所以由v-t图可直接读出物体在各个不同时刻的速度,得知物体的运动情况.
利用图线与坐标轴围住的面积求路程和位移.在计算物体的位移时,要注意图象的“面积”有正负之分,在横轴上面的面积为正,说明位移为正,在横轴下面的面积为负,说明位移为负.
解析:(1)汽车在OA段做匀加速直线运动,在AB段做匀速直线运动,BC段做匀减速直线运动,在CD段处于静止状态.DE段表示反向加速,EF段表示又做加速运动.
(2)汽车在全程中所通过路程d在数值上等于图中梯形OABC和三角形DEF面积之和,即路程d=275m,位移s=-25m.
也就是汽车最终位置在出发点后边25m处.
合作讨论
龟兔赛跑是大家在小时候就听过的故事,请叙述故事梗概并画出龟兔的s-t图和v-t图.
我的思路:可以认为乌龟一直做速度很小的匀速运动,而兔子则是先做加速运动,然后开始睡觉,停止不动,发现乌龟超过自己后再加速追赶.
解析:兔子先快速跑了一段,然后看到乌龟没有追上来,就躺在树下睡起了大觉,醒来时,还没有见到乌龟,它以为乌龟还在后面,其实乌龟一直在匀速运动,此时已快到终点了.s-t图和v-t图如下:

图1-4
变式训练
3.匀加速直线运动的图象
对汽车的启动,通过速度计记下每隔5s各时刻的速度,列表如下,可作出如图的速度图象。

结论:匀加速直线运动的速度一时间图象是一条斜向上倾斜的直线.
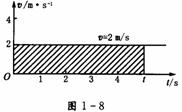 1.匀速直线运动的速度一时间图象从速度一时间图象这个叫法看,是速度与时间的关系图象,以t轴为横轴,v轴为纵轴,建立坐标系.而匀速直线运动的速度v不随时间变化,只能是与t轴平行的直线.
1.匀速直线运动的速度一时间图象从速度一时间图象这个叫法看,是速度与时间的关系图象,以t轴为横轴,v轴为纵轴,建立坐标系.而匀速直线运动的速度v不随时间变化,只能是与t轴平行的直线.
从图象中可获得:
(1)速度的大小、方向
(2)从s=vt可获得:边长为v和t所围成的矩形的面积,就是物体在时间t内的位移.(即图中的斜线阴影部分)
2.匀变速直线运动特征
匀变速直线运动:在变速直线运动中,如果在相等时间内速度的改变相等.这种运动叫做匀变速直线运动.
(1)匀加速直线运动:在变速直线运动中,如果速度随时间均匀增加,称为匀加速直线运动.如汽车的启动、飞机的起飞、石块的自由下落、滑块沿斜面加速下滑等可近似认为是匀加速直线运动.
(2)匀减速直线运动:在变速直线运动中,如果速度随时间均匀减小,称为匀减速直线运动.如汽车刹车、飞机降落、石块上抛、滑块沿斜面上滑等可近似认为是匀减速直线运动.
1.在匀速直线运动中,位移s跟发生这段位移所用的时间t成正比.
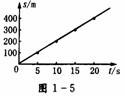 2.用图象表示位移和时间的关系.
2.用图象表示位移和时间的关系.
在平面直角坐标系中纵轴表示位移s,横轴表示时间t,s-t图象如图1-5所示.
可见匀速直线运动的位移和时间的关系图象是一条倾斜直线,这种图象叫做位移一时间图象(s-t图象).
图象的含义:
①表明在匀速直线运动中,s与t成正比.
②图象上任一点的横坐标表示运动的时间,对应的纵坐标表示位移.
③图象的斜率k=△s/△t=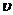 .
.
[例1]判断下列位移一时间图象中物体如何运动.
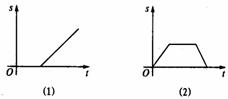
图1-6
 解析:(1)物体先静止一段时间,再做匀速直线运动.
解析:(1)物体先静止一段时间,再做匀速直线运动.
(2)物体先做匀速直线运动,静止一段时间后再反方向做匀速直线运动,且反方向的匀速直线运动的速率大.
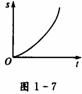
另外,当物体做变速直线运动时(物体在一条直线上运动,如果在相等的时间里位移不相等,这种运动就叫做变速直线运动.例如飞机起飞、火车进站等),变速直线运动的位移一时间图象不是直线而是曲线(如图1-7).
2.利用速度图线很容易找出例6中的位移之比.如图2所示,从t=0开始,在t轴上取相等的时间间隔,并从等分点作平行于速度图线的斜线,把图线下方的面积分成许多相同的小三角形.于是,立即可得:从t=0起,在t、2t、3t、…内位移之比为
s1∶s2∶s3…=1∶4∶9…
在第1个t、第2个t、第3个t、…内位移之比为
sⅠ∶sⅡ∶sⅢ∶…=1∶3∶5∶…
[例7] 一辆沿平直路面行驶的汽车,速度为36km/h.刹车后获得加速度的大小是4m/s2,求:
(1)刹车后3s末的速度;
(2)从开始刹车至停止,滑行一半距离时的速度.
[分析] 汽车刹车后作匀减速滑行,其初速度v0=36km/h=10m/s,vt=0,加速度a=-4m/s2.设刹车后滑行t s停止,滑行距离为S,其运动示意图如图所示.

[解](1)由速度公式vt=v0+at得滑行时间:
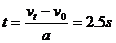
即刹车后经2.5s即停止,所以3s末的速度为零.
(2)由位移公式得滑行距离.即
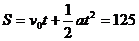 m
m
设滑行一半距离至B点时的速度为vB,由推论
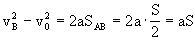
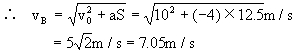
[说明](1)不能直接把t=3 s代入速度公式计算速度,因为实际滑行时间只有2.5s.凡刹车滑行一类问题,必须先确定实际的滑行时间(或位移);(2)滑行一半距离时的速度不等于滑行过程中的平均速度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com