
1.定义:只受重力作用,从静止开始的下落运动。
推论1.物体作初速度为零的匀加速直线运动,从开始(t=0)计时起,在连续相邻相等的时间间隔(△t=1s)内的位移比为连续奇数比。即:
S第1s内∶S第2s内∶S第3s内…=1∶3∶5∶…
例6.一个物体从塔顶作自由落体运动,在到达地面前最后1s内发生的位移是总位移的7/16,求塔高。(g取10m/s2)
解:由位移的比例关系式,可求得物体第4s内的位移。
即由S第4s内:S第1s内=7:1得S第4s内=7S第1s内
4s内的总位移
S4=S第1s内+S第2s内+S第3s内+S第4s内
=S第1s内+3S第1s内+5S第1s内+7S第1s内=16S第1s内
注意到物体在到达地面前1s内的位移是总位移的7/16,即
S第4s内/S4=7/16,
可知物体下落的总时间t总=4s,故塔高
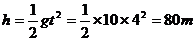
推论2.物体作匀加速(加速度为a)直线运动,它经历的两个相邻相等的时间间隔为T,它在这两个相邻相等的时间间隔内的位移差为△S,则有△S=aT2。
例7.有一个作匀加速直线运动的质点,它在两个连续相等的时间间隔内所发生的位移分别为10m和16m,时间间隔为2s,求该质点运动的加速度a。
解:由△S=aT2可得
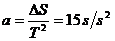
推论3.物体作初速度为零的匀加速直线运动,从初始位置(S=0)开始,它通过连续相邻相等的位移所需的时间之比为
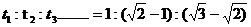
例8.一粒子弹恰能穿过三块相同的固定的木板,设子弹在木板里运动的加速度恒定,则子弹分别穿过三块木板所用时间之比是:多少?
解:将子弹运动看成“反向”作初速度为零的匀加速运动。由时间的比例关系得:子弹分别穿过三块等厚的木板所用时间之比为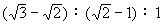
例5.一小划船以大小不变的划速v1在静水中从甲地到乙地,再立即从乙地返回甲地,往返总时间为t1;若河水流动,且水流速度恒定不变,大小为v2(≠0),该小划船以大小不变的划速v1从甲地顺流而下划至乙地,再立即逆流而上从乙地划向甲地。往返总时间为t2,则 [ ]
A.t2一定大于t1;
B.t2一定等于t1;
C.t2一定小于t1
D.t2不是等于t1就是小于t1
解:可设想水流速度v2趋于无穷大,则船从甲地顺流而下划至乙地后,须经过无限长时间才能从乙地划至甲地,从而否定了选项B,C,D。本题的正确选顶是A。
研究物体运动必须选择参考系,根据问题的特点选择好参考系,能使解题大大简化。
例4.有一升降机在向上作加速度为a=2.2m/s2的匀加速直线运动。某一时刻,有一颗螺钉从升降机的顶部脱落,若升降机顶部到底板的高度h=6m,求螺钉落到底板所需的时间。(空气阻力不计,g=9.8m/s2)
解:设螺钉刚开始脱落时,升降机向上的速度为v,螺钉也具有向上的速度v,以升降机为参照物,螺钉相对升降机底板的初速度v0相=0,螺钉相对升降机底板的加速度a相=a+g=2.2+9.8=12m/s2,螺钉相对升降机底板的位移S相=h=6m,由
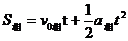
并注意到v0相=0,可得
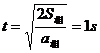
在空气阻力不计的情况下,竖直上抛运动有速度的对称性:抛体经任一高度时,上升和下落的速度大小相等,方向相反;时间对称性:抛体在通过任一段竖直距离时,上升和下落的时间相等。
例3.一个从地面竖直上抛的物体,不计空气阻力,它两次经过一个较低点A的时间间隔是5s,两次经过一个较高点B的时间间隔是3s,则AB间距离为多少?(g=10m/s2)
解:由竖直上抛运动的过程的对称性可知:抛体从最高点返回到
A点的时间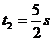 ,所以AB=
,所以AB= m
m
例2.升降机由静止开始匀加速竖直上升2s, 速度达到4m/s后,匀速竖直上升5s,接着匀减速竖直上升3s才停下来。求升降机在题述过程中发生的总位移S=?
解:依题意,作出升降机的速度一时间图线,如附图所示。梯形OABC的“面积”即等于题中所求的位移S。
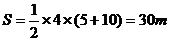
例1.一物体在水平地面上由静止开始受到一水平拉力作用,匀加速前进10m后,撤去这个水平拉力,物体又向前滑行50m才停止。求该物体在这两个阶段中运动时间之比t1∶t2。
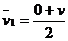
式中的v为第一阶段的末速度,物体在第二阶段的平均速度为
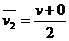
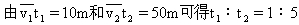
2、过程按位移等分
如果把一个初速度为零的匀加速直线运动过程分成许多位移相等的阶段(如图所示),设每一个阶段的时间T,由位移公式x= 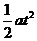
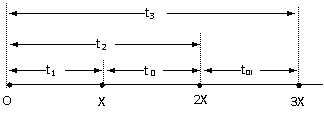 通过前1个X内的时间为t1=
通过前1个X内的时间为t1=
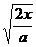
通过前2个X内的时间为t2=

通过前3个X内的时间为t3=
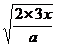
…………………………
可以看出t1:t2 :t3:……=1: :
: :……连续的自然数平方根比
:……连续的自然数平方根比
通过第1个X内的时间为t1=
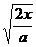
通过第2个X内的时间为tⅡ= t2- t1= -
-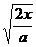 =(
=( -1)
-1)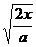
通过第3个X内的时间为tⅢ= t3- t2= 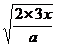 -
- =(
=( -
- )
)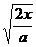
…………………………
可以看出t1:tⅡ
:tⅢ:……=1:( -1):(
-1):( -
- ):……
):……
[例2]:一物体从斜面顶端由静止开始匀加速下滑,经过1s到达斜面中点,问:还要经过多长时间到达斜面底端?
[解析]:斜面中点把物体运动的位移分为两等份,则t1:tⅡ
=1:( -1),所以
-1),所以
tⅡ =( -1)s=0.41s,即物体还要经过0.41s到达斜面底端。
-1)s=0.41s,即物体还要经过0.41s到达斜面底端。
[问题探究]:物体在中点前后两个过程的平均速度之比为多少?
[例3]一个做匀变速直线运动的质点在1-4s内通过的位移分别是24 m,5-8s内通过的位移64 m,求质点的初速度和加速度大小。
[解析]:[方法1]:由位移公式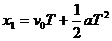 ,
,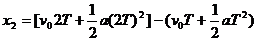
将x1=24m,x2=64m,T=4s代入两式求得v0=1m/s, =2.5 m/s2.
=2.5 m/s2.
[方法2]:用公式△x= T2求解:由△x = x2-x1=
T2求解:由△x = x2-x1= T2得
T2得 =
=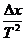 =
=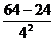 m/s2=2.5 m/s2
m/s2=2.5 m/s2
再代入x1=v0T+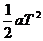 可求得v0=1m/s.
可求得v0=1m/s.
[方法3]:用时间中点速度等于平均速度求解:
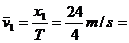 6 m/s
这个速度就是2s末瞬时速度
6 m/s
这个速度就是2s末瞬时速度
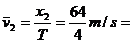 16 m/s这个速度就是6s末瞬时速度
16 m/s这个速度就是6s末瞬时速度
 =
=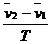 =
=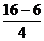 m/s2=2.5 m/s2, 再由
m/s2=2.5 m/s2, 再由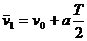 求得v0=1 m/s.
求得v0=1 m/s.
此题还有其它解法,想一想还有什么方法?
初速度为零的匀加速直线运动是一种特殊的匀变速直线运动,这种运动的规律公式为:
vt=  t, x=
t, x=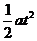 , x=
, x=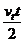 ,
, 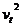 =2
=2
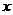
1、过程按时间等分
如果把一个初速度为零的匀加速直线运动过程分成许多时间相等的阶段(如第1秒、第2秒、第3秒……),当然每一个阶段的时间不一定是1秒,设每一个阶段的时间T,由位移公式x=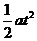
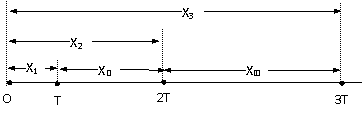 前1个T内的位移为X1=
前1个T内的位移为X1=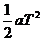
前2个T内的位移为X2=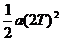
前3个T内的位移为X3=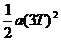
…………………………
可以看出X1:X2 :X3:……=12:22:32:……连续的自然数平方比
第1个T内的位移为X1=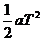
第2个T内的位移为XⅡ= X2-X1 =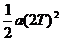 -
-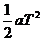 =
=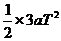
第3个T内的位移为XⅢ= X3-X2 =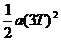 -
-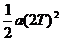 =
=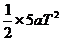
…………………………
可以看出X1:XⅡ :XⅢ:……=1:3:5:……连续的奇数比
[问题探究]:你能用图象来推导上面的结论吗?试一试。
[例1]:一个质点做初速度为零的匀加速直线运动,已知质点在第2s内的位移为0.6m,则质点在第5s内的位移为多少?
[解析]:因为XⅡ :XV=3:9=1:3,所以XV=3×XⅡ=3×0.6m=1.8m.
[问题探究]:质点在前5s内的位移为多少?
4.一物体做匀变速直线运动,第2s内的位移为4m,第5s内的位移为10 m,求物体的加速度.
[解析]:把物体的运动过程分成许多时间相等的阶段,每个阶段的时间为1秒,设相邻两秒内的位移之差为△x,则
△x=xⅢ-xⅡ
△x=xⅣ-xⅢ
△x=xⅤ-xⅣ
把各式相加得xⅤ-xⅡ=3△x,即△x= 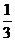 (xⅤ-xⅡ)=2m.
(xⅤ-xⅡ)=2m.
所以 =
=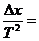 2 m/s2
2 m/s2
[问题探究1]:物体在第9秒内的位移为多大?
物体第3秒位移比第2秒位移大1个△x,第4秒位移比第2秒位移大2个△x,第5秒位移比第2秒位移大3个△x……第9秒位移比第2秒位移大7个△x,则第9内物体的位移为
x=7×△x=7×2m=14m.
[问题探究2]:如何求物体在开始计时的初速度?
点拔:[方法1]:根据物体在相邻相等时间内的位移之差是一定值,第1秒位移比第2秒位移小2m,则第1秒位移为2m,对第1秒过程:x=2m、t=1s、 =2 m/s2. 由位移公式
=2 m/s2. 由位移公式
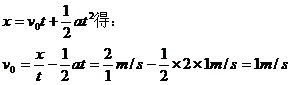
即初速度为1m/s。
[方法2]:第2秒位移为4m,则第2秒的平均速度为4m/s,这个速度就是第1.5秒末瞬时速度。对1.5秒过程:t=1.5s、vt=4m/s 、 =2 m/s2.由速度公式vt=v0+
=2 m/s2.由速度公式vt=v0+ t得
t得
v0=vt- t=4m/s-2×1.5 m/s=1m/s。
t=4m/s-2×1.5 m/s=1m/s。
讨论:此题还有哪些解题方法,先试一试。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com