有些题看似不同，但确有相同的求解方法，实质是一样的，将这些题放在一起比较有利于提高同学们分析问题、解决问题的能力，能达到举一反三的目的。

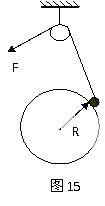
例9、如图15所示，光滑大球固定不动，它的正上方有一个定滑轮，放在大球上的光滑小球(可视为质点)用细绳连接，并绕过定滑轮，当人用力F缓慢拉动细绳时，小球所受支持力为N，则N，F的变化情况是：

A、都变大；

B、N不变，F变小；

C、都变小；

D、N变小， F不变。

例10、如图16所示，绳与杆均轻质，承受弹力的最大值一定，A端用铰链固定，滑轮在A点正上方(滑轮大小及摩擦均可不计)，B端吊一重物。现施拉力F将B缓慢上拉(均未断)，在AB杆达到竖直前

A、绳子越来越容易断，

B、绳子越来越不容易断，

C、AB杆越来越容易断，

D、AB杆越来越不容易断。

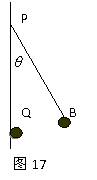
例11、如图17所示竖直绝缘墙壁上的Q处有一固定 的质点A，Q正上方的P点用丝线悬挂另一质点B， A、B两质点因为带电而相互排斥，致使悬线与竖直方向成θ角，由于漏电使A、B两质点的带电量逐渐减小。在电荷漏完之前悬线对悬点P的拉力大小:　

A、保持不变；

B、先变大后变小；

C、逐渐减小；

D、逐渐增大。

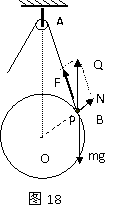分析与解：例9、例10、例11三题通过受力分析发现，物理实质是相同的，即都是三力平衡问题，都要应用相似三角形知识求解。

在例中对小球进行受力分析如图18所示，显然ΔAOP与ΔPBQ相似。 由相似三角形性质有：(设OA=H，OP=R，AB=L)　　　　　　　　　　　　　　　　　　　　　　　　

　　　 　　　　　　　　　　　　　　　　　　　　　

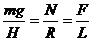
　因为mg、H、R都是定值，所以当L减小时，N不变，F减小。B正确。同理可知例10、例11的答案分别为B和A

2.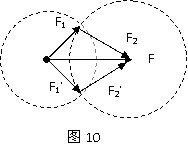已知两个不平行分力的大小。如图10所示，分别以F的始端、末端为圆心，以F₁、F₂为半径作圆，两圆有两个交点，所以F分解为F₁、F₂有两种情况。存在极值的几种情况。

(1)已知合力F和一个分力F₁的方向，另一个分力F₂存在最小值。

(2)已知合力F的方向和一个分力F₁，另一个分力F₂存在最小值。

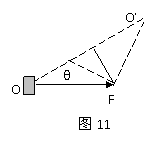例7、如图11所示，物体静止于光滑的水平面上，力F作用于物体O点，现要使合力沿着OO^，方向，那

么，必须同时再加一个力F^，。这个力的最小值是：

A、Fcos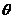,　　　　　 B、Fsinθ,

C、Ftanθ,　　　　　　　　　　　　　　　　 D、Fcotθ

分析与解：由图11可知，F^，的最小值是Fsinθ,即B正确。

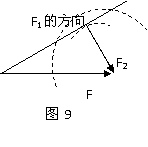
1.已知一个分力F₁的方向和另一个分力F₂的大小，由图9可知：　　　　　　　　　　　　　　　　　　　　　

当F₂=Fsin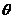时，分解是唯一的。

当Fsin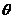<F₂<F时，分解不唯一，有两解。当F₂>F时，分解是唯一的。

将一个已知力F进行分解，其解是不唯一的。要得到唯一的解，必须另外考虑唯一性条件。常见的唯一性条件有：

1.已知两个不平行分力的方向，可以唯一的作出力的平行四边形，对力F进行分解，其解是唯一的。

2已知一个分力的大小和方向，可以唯一的作出力的平行四边形，对力F进行分解，其解是唯一的。

力的分解有两解的条件：

有n个力F₁、F₂、F₃、……F_n,它们合力的最大值是它们的方向相同时的合力，即F_max=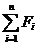.而它们的最小值要分下列两种情况讨论：

(1)、若n个力F₁、F₂、F₃、……F_n中的最大力F_m大于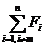，则它们合力的最小值是(F_m-)。

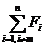(2)若n个力F₁、F₂、F₃、……F_n中的最大力F_m小于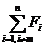，则它们合力的最小值是0。

例5、四个共点力的大小分别为2N、3N、4N、6N，它们的合力最大值为 　　　，它们的合力最小值为　　　　　 。

　　 分析与解：它们的合力最大值F_max=(2+3+4+6)N=15N.因为F_m=6N<(2+3+4)N,所以它们的合力最小值为0。

例6、四个共点力的大小分别为2N、3N、4N、12N，它们的合力最大值为　 ，它们的合力最小值为　　　　　 。

　　 分析与解：它们的合力最大值F_max=(2+3+4+12)N=21N，因为F_m=12N>(2+3+4)N,所以它们的合力最小值为(12-2-3-4)N=3N。

直接接触的物体间由于发生弹性形变而产生的力叫弹力。弹力产生的条件是“接触且有弹性形变”。若物体间虽然有接触但无拉伸或挤压，则无弹力产生。在许多情况下由于物体的形变很小，难于观察到，因而判断弹力的产生要用“反证法 ”，即由已知运动状态及有关条件，利用平衡条件或牛顿运动定律进行逆向分析推理。

例如，要判断图5中静止在光滑水平面上的球是否受到斜面对它的弹力作用，可先假设有弹力N₂存在，则此球在水平方向所受合力不为零，必加速运动，与所给静止状态矛盾，说明此球与斜面间虽接触，但并不挤压，故不存在弹力N₂。

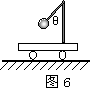例4、如图6所示，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆下端固定有质量为m的小球，下列关于杆对球的作用力F的判断中，正确的是：

A．小车静止时，F=mgsinθ,方向沿杆向上。

B．小车静止时，F=mgcosθ,方向垂直杆向上。

C．小车向右以加速度a运动时，一定有F=ma/sinθ.

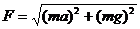D.小车向左以加速度a运动时，,方向斜向左上方，与竖直方向的夹角为α=arctan(a/g).

分析与解：小车静止时，由物体的平衡条件知杆对球的作用力方向竖直向上，且大小等于球的重力mg.

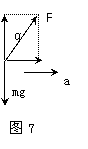
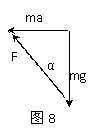小车向右以加速度a运动，设小球受杆的作用力方向与竖直方向的夹角为α,如图7所示。根据牛顿第二定律有：Fsinα=ma,　 Fcosα=mg.，两式相除得：tanα=a/g.

只有当球的加速度a=g.tanθ时，杆对球的作用力才沿杆的方向，此时才有F=ma/sinθ.小车向左以加速度a运动，根据牛顿第二定律知小球所受重力mg和杆对球的作用力F的合力大小为ma，方向水平向左。根据力的合成知三力构成图8所示的矢量三角形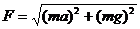，,方向斜向左上方，与竖直方向的夹角为：α=arctan(a/g).

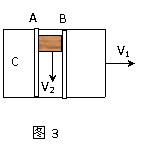滑动摩擦力的方向总是与物体“相对运动”的方向相反。所谓相对运动方向，即是把与研究对象接触的物体作为参照物，研究对象相对该参照物运动的方向。当研究对象参与几种运动时，相对运动方向应是相对接触物体的合运动方向。静摩擦力的方向总是与物体“相对运动趋势”的方向相反。所谓相对运动趋势的方向，即是把与研究对象接触的物体作为参照物，假若没有摩擦力研究对象相对该参照物可能出现运动的方向。

例3、如图3所示，质量为m的物体放在水平放置的钢板C上，与钢板的动摩擦因素为μ。由于受到相对于地面静止的光滑导槽A、B的控制，物体只能沿水平导槽运动。现使钢板以速度V₁向右匀速运动，同时用力F拉动物体(方向沿导槽方向)使物体以速度V₂沿导槽匀速运动，求拉力F大小。

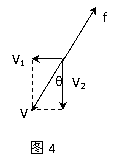　 分析与解：物体相对钢板具有向左的速度分量V₁和侧向的速度分量V₂，故相对钢板的合速度V的方向如图4所示，滑动摩擦力的方向与V的方向相反。根据平衡条件可得:

　　 F=fcosθ=μmg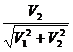

从上式可以看出：钢板的速度V₁越大，拉力F越小。

问题一：弄清滑动摩擦力与静摩擦力大小计算方法的不同。

当物体间存在滑动摩擦力时，其大小即可由公式F_μ=μF_N计算，由此可看出它只与接触面间的动摩擦因数及正压力有关，而与相对运动速度大小、接触面积的大小无关。

正压力是静摩擦力产生的条件之一，但静摩擦力的大小与正压力无关(最大静摩擦力除外)。当物体处于平衡状态时，静摩擦力的大小由平衡条件或牛顿定律求解；而物体处于非平衡态的某些静摩擦力的大小应由牛顿第二定律求解。

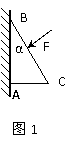
例1、如图1所示，质量为m，横截面为直角三角形的物块ABC，，AB边靠在竖直墙面上，F是垂直于斜面BC的推力，现物块静止不动，则摩擦力的大小为_________。

　　 分析与解：物块ABC受到重力、墙的支持力、摩擦力及推力四个力作用而平衡，由平衡条件不难得出静摩擦力大小为

　　 。

例2、如图2所示，质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上，P、Q之间的动摩擦因数为μ₁，Q与斜面间的动摩擦因数为μ₂。当它们从静止开始沿斜面滑下时，两物体始终保持相对静止，则物体P受到的摩擦力大小为：

A．0；　　　　　 B. μ₁mgcosθ;　　　

C.μ₂mgcosθ;　　　　 D. (μ₁+μ₂)mgcosθ;

分析与解：当物体P和Q一起沿斜面加速下滑时，其加速度为：a=gsinθ-μ₂gcosθ.

因为P和Q相对静止，所以P和Q之间的摩擦力为静摩擦力，不能用公式求解。对物体P运用牛顿第二定律得： mgsinθ-f=ma

所以求得：f=μ₂mgcosθ.即C选项正确。

4．一题多解能训练大家的发散思维，对能力有较高的要求．

这些方法在其它内容上也有用，希望大家用心体会．

[例题2]甲、乙、丙三辆汽车以相同的速度同时经过某一路标，从此时开始甲车一直做匀速直线运动，乙车先加速后减速，丙车先减速后加速，它们经过下个路标时速度又相同．则：[　　 ]

A．甲车先通过下一个路标

B．乙车先通过下一个路标

C．丙车先通过下一个路标

D．条件不足，无法判断

点拨：直接分析难以得出答案，能否借助图像来分析？

(学生讨论发言，有些学生可能会想到用图像．)

解答：作出三辆汽车的速度-时间图像：

甲、乙、丙三辆汽车的路程相同，即速度图线与t轴所围的面积相等，则由图像分析直接得出答案B．

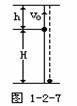[例题3]一跳水运动员从离水面10m高的平台上向上跃起，举双臂直体离开台面，此时其重心位于从手到脚全长的中点，跃起后重心升高0.45m达到最高点，落水时身体竖直，手先入水(在此过程中运动员水平方向的运动忽略不计)，从离开跳台到手触水面，他可用于完成空中动作的时间是______s．(计算时，可以把运动员看作全部质量集中在重心的一个质点．g取10m/s2，结果保留二位数字．)分析：首先，要将跳水这一实际问题转化为理想化的物理模型，将运动员看成一个质点，则运动员的跳水过程就抽象为质点的竖直上抛运动．

学生解答：

解法一：分段求解．

上升阶段：初速度为v0，a=-g的匀减速直线运动

由题意知质点上升的最大高度为：

h=0.45m

可求出质点上抛的初速度

上升时间：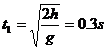

下落阶段：为自由落体运动，即初速度为0，a=g的匀加速直线运动．

下落时间：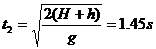

完成空中动作的时间是：

t₁+t₂=0.3+1.45=1.75s

解法二：整段求解．

先求出上抛的初速度：

v₀=3m/s(方法同上)

将竖直上抛运动的全过程看作统一的匀减速直线运动，设向上的初速度方向为正，加速度a=-g，从离开跳台到跃入水中，质点位移为-10m．

由位移公式: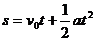 代入数据：

　　　　　

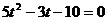
求出：t=1.75s(舍去负值)

通过计算，我们体会到跳水运动真可谓是瞬间的体育艺术，在短短的1.75s内要完成多个转体和翻滚等高难度动作，充分展示优美舒展的姿势确实非常不易．

[例题4]在平直公路上有甲、乙两辆车在同一地点向同一方向运动，甲车以10m/s的速度做匀速直线运动，乙车从静止开始以1.0m/s的加速度作匀加速直线运动，问：

(1)甲、乙两车出发后何时再次相遇？

(2)在再次相遇前两车何时相距最远？最远距离是多少？

要求用多种方法求解．

学生分析与解答：

解法一：函数求解．

出发后甲、乙的位移分别为

s_甲=vt=10t　　　　　　　　　　　　　　　　　　　 　①

两车相遇：s_甲=s_乙　　　　 　　　　　　　　　　　　　　　　　③

解出相遇时间为：t=20s

两车相距：△s=s_甲-s_乙=10t-0.5t2

求函数极值：当t=10s时，△s有最大值，△s_max=50m

微机模拟物理过程(几何画板)：

观察：△s的变化

现象：当v_乙＜v_甲时，△s增大

当v_乙＞v_甲时，△s减小

当v_乙=v_甲时，△s最大

根据学生分析情况适当提示．

解法二：实验方法求△smax．

当v_乙=v_甲时，△s最大，

有：at=10，t=10/1=10(s)

△smax=s_甲-s_乙=10t-0.5t2=50(m)

解法三：图像法．

分别作出甲、乙的速度-时间图像

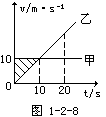
当甲、乙两车相遇时，有s_甲=s_乙，

由图像可看出：当甲图线与时间轴所围面积=乙图线与时间轴所围面积时，有：

t=20s，即两车相遇的时间．

当v_乙=v_甲时，△s最大．

由图像可看出：△smax即为阴影部分的三角形面积，

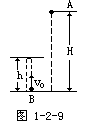[例题5]球A从高H处自由下落，与此同时，在球A下方的地面上，B球以初速度v₀竖直上抛，不计阻力，设v0=40m/s，g=10m/s²．试问：

(1)若要在B球上升时两球相遇，或要在B球下落时两球相遇，则H的取值范围各是多少？

(2)若要两球在空中相遇，则H的取值范围又是多少？

示意图：图1-2-9．

分析：若H很小，可能在B球上升时相遇；若H较大，可能在B球下落时相遇，但若H很大，就可能出现B球已落回原地，而A球仍在空中，即两球没有相遇．所以，要使两球在空中相遇．H要在一定的范围内．

微机模拟(几何画板)：

v₀=40m/s

设定H取不同的值，观察两球在什么位置相遇、或不相遇：

H=100m时，在B球上升时相遇

H=200m时，在B球下落时相遇

H=400m时，不相遇

再改变几次H的值进行观察．

微机模拟：

H不变，改变v₀

当v₀取不同的值，观察两球在什么位置相遇或不相遇．

请同学们课后解答．

学生解答：

(1)算出B球上升到最高点的时间：

t₁=v₀/g=40/10=4(s)

则B球在最高点处两球相遇时：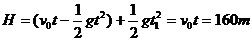

B球在落地前瞬间两球相遇时：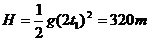

所以：

要在B球上升时两球相遇，则0＜H＜160m

要在B球下落时两球相遇，则160m＜H＜320m．

(2)由上可知，若要两球在空中相遇，则0＜H＜320m．