
4.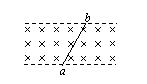 如图所示,宽为d的匀强磁场的磁感应强度为B,方向垂直于纸面向里.现有一个电量为-q,质量为m的粒子(不计重力),从a点以垂直于磁场边界PQ并垂直于磁场的方向射入磁场,然后从磁场上边界MN上的b点射出磁场.已知ab连线与PQ成60º,求该带电粒子射出磁场时的速度大小。
如图所示,宽为d的匀强磁场的磁感应强度为B,方向垂直于纸面向里.现有一个电量为-q,质量为m的粒子(不计重力),从a点以垂直于磁场边界PQ并垂直于磁场的方向射入磁场,然后从磁场上边界MN上的b点射出磁场.已知ab连线与PQ成60º,求该带电粒子射出磁场时的速度大小。
2.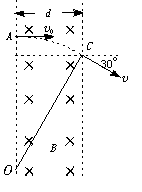 如图所示,一束电子(电量为e)以速度v0垂直射入磁感应强度为B,宽为d的匀强磁场中,穿出磁场时速度方向与电子原来入射方向的夹角为30°,则电子的质量是多少?穿过磁场的时间是多少?
如图所示,一束电子(电量为e)以速度v0垂直射入磁感应强度为B,宽为d的匀强磁场中,穿出磁场时速度方向与电子原来入射方向的夹角为30°,则电子的质量是多少?穿过磁场的时间是多少?
[方法指导]一定要先画好辅助线(半径、速度及延长线)。偏转角由sinθ=L/R求出。侧移由R2=L2-(R-y)2解出。经历时间由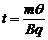 得出。
得出。

注意,这里射出速度的反向延长线与初速度延长线的交点不再是宽度线段的中点,这点与带电粒子在匀强电场中的偏转结论不同!
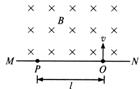
3(7分)、下图中MN表示真空室中垂直于纸面的平板,它的一侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度大小为B.一带电粒子从平板上的狭缝O处以垂直于平板的初速v射入磁场区域,最后到达平板上的P点.已知B、v以及P到O的距离l,不计重力,求此粒子的比荷(粒子的电荷量与质量的比值).
解: 粒子初速v垂直于磁场,粒子在磁场中受洛伦兹力而做匀速圆周运动,设其半径为R ,由洛伦兹力公式和牛顿第二定律,有
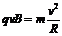 ………①………………………(3分)
………①………………………(3分)
因粒子经O点时的速度垂直于OP,故OP 是直径 .得
 …………②……………………………(2分)
…………②……………………………(2分)
由此得  ……………………………(2分)
……………………………(2分)
19、大于eBd / m
1. 如图所示,比荷(荷质比)为e / m的电子从左侧垂直于界面、垂
如图所示,比荷(荷质比)为e / m的电子从左侧垂直于界面、垂
直于磁场射入宽度为d、磁感受应强度为B的匀强磁场区域,要从右侧面
穿出这个磁场区域,电子的速度应满足的条件是 。
1. 三个速度大小不同的同种带电粒子,沿同一方向从如图所示的长方形区域的匀强磁场
上边缘射入强磁场,当它们从下边缘飞出时对入射方向的偏角分别为90°、60°、
30°,则它们在磁场中的运动时间之比 ( )
 A.1∶1∶1
A.1∶1∶1
B.1∶2∶3
C.3∶2∶1
D.1∶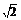 ∶
∶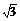
答案 C
(1)速度垂直边界
1、平行边界
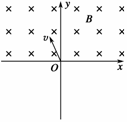
6、如图3-6-2所示,在y<0的区域内存在匀强磁场,磁场方向垂直平面并指向纸面外,磁感应强度为B.一带正电的粒子(不计重力)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.若粒子射出磁场的位置与O点的距离为,求该粒子的电荷量与质量之比q/m.
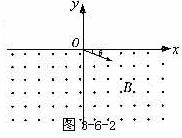
解析:洛伦兹力提供向心力Bqv=mv2/r……①
几何关系如图3-6-3所示,l/2=rsinθ……②
整理得q/m=2v0sinθ/lB……③
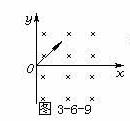
5、如图3-6-9所示,一个带负电的粒子以速度v由坐标原点射入充满x正半轴的磁场中,速度方向与x轴、y轴均成45°角.已知该粒子电量为-q,质量为m,则该粒子通过x轴和y轴的坐标分别是多少?
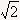 mv/qB -
mv/qB -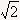 mv/qB
mv/qB
4. 如图所示,在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场,一个不计
重力的带电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直
于磁场且与x轴正方向成120°角,若粒子穿过y轴正半轴后在磁场中到x轴的最大距
离为a,则该粒子的荷质比和所带电荷的正负是
 ( )
( )
A.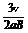 ,正电荷 B.
,正电荷 B.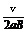 ,正电荷
,正电荷
C.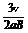 ,负电荷 D.
,负电荷 D. 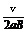 ,负电荷
,负电荷
答案 C
3. 如图所示,直线边界MN上方有垂直纸面向里的匀强磁场,磁感应强度为B,磁场区域足够大.今有质量为m,电荷量为q的正、负带电粒子,从边界MN上某点垂直磁场方向射入,射入时的速度大小为v,方向与边界MN的夹角的弧度为θ,求正、负带电粒子在磁场中的运动时间.
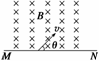 答案 带正电粒子:2m(π-θ)/qB 带负电粒子:
答案 带正电粒子:2m(π-θ)/qB 带负电粒子: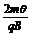
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com