《初中数学课程标准(实验稿)》. 人民教育出版社

《八年级数学教科书》. 人民教育出版社

《数理化生学习大全》. 上海教育出版社

《满分训练法》. 数学 . 八年级(上). 出版社

数学证明本身的学习包括：获得或质疑需要证明的命题；理解命题的结构，特别是条件与结论之间的逻辑联系；获得完成证明的基本策略。在教学活动中，让学生能关注知识的发生过程而不仅仅是结论，不去为做题而做题是素质教育的要求，更是学科发展的根基。“义务教育阶段数学课程的主要任务不是培养数学家；但是，我们的数学课程不能给那些未来数学家的成长制造障碍。”这是一位老数学教师的话，放在这里作为本文的结尾，与各位数学教师共勉！

2、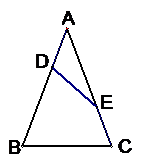已知：在△ABC中，AB=AC，AD=CE

求证：DE≥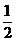BC

分析：读题：AB=AC，AD=CE

　　　 结论：BD=AE

　　　 读图：AD与AE在一个三角形中，

∠A是它们的夹角

　　　 设问：在等式的另一边，CE与BD是否能够放在一个三角形中？

　　　 发现：可以采用平移法，平移CE或BD都可以，下面以平移BD为例继续说明

　　　 行动：平移BD，使点B与点C 重合，把平移后的D点记为F，∠ECF是它们的夹角，且∠ECF=∠A　 (两直线平行，内错角相等)

　　　　　　 连接EF，发现可以证明三角形全等，则DE=EF

　　　 转化：欲证DE≥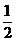BC，只需证DE+EF≥BC

　　　 观察：在△DEF中DE+EF≥DF，而DF=BC

上述分析主要是训练学生的读题与读图相结合的能力，在此过程中用到了直线的平移以及线段的代换、简单的不等式的性质。共做了三条辅助线，且辅助线有的在形外，有的与形相交。

完整的证明过程如下：

证明：过C作CF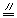BD,连接EF，DF,

　　　 在△ADE和△CEF中

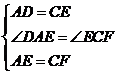
　　 　∴△ADE≌△CEF(SAS)

　　　 DE=EF(全等三角形的对应边相等)

又∵DE+EF≥DF, DF=BC

∴DE≥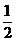BC

1、已知：在△ABC中，AB>AC,　 AD平分∠BAC

求证：AB-AC>BD-DC

分析：读题：AB>AC，

　　　 设问：AB比AC大多少？

　　　 行动：比长度

　　　 设问：将AB与AC的哪一端固定在一起，比较另一端好呢？如何比？

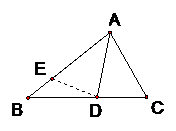　　　 发现：A为公共端点，可采用旋转法

　　　 行动：将AC绕A点旋转，使AC与AB在同一直线上，将C在AB上的落点记为E

　　　 结论：AC=AE ，AB-AC=BE，

原命题转化为求证BE>BD-DC　 (1)

　　　　 观察：BE与BD可以放在一个三角形中

　　　　 行动：连接DE

　　　　 观察：在△BED中，BE>BD-DE，对比(1)式，注意到DC与DE

　　　 读题：AD平分∠BAC

　　　 结论：∠EAD=∠CAD，恰可用于证明三角形全等(SAS)

上述分析主要是训练学生的读题与读图相结合的能力，在此过程中用到了直线的旋转以及线段的代换。共做了一条辅助线，且辅助线在形内。

完整的证明过程如下：

证明：∵AB>AC

　　 　∴可在AB上截取AE=AC

　　　 在△AED和△ACD中

　　 　∴△AED≌△ACD(SAS)

　　　 ED=CD(全等三角形的对应边相等)

∵AB-AE=BE>BD-DE

　　 　∴AB-AC>BD-DC

4、由等式的性质迁移出简单的不等式的性质

例如:如果a>b，那么a+a>b+b

　　 如果a>b, 那么a+c>b+c

　　 如果a>b,b>c,那么a>b>c

……

3、训练读题与读图相结合的能力：

这是确定位置关系变换方法的关键

2、通过典型习题深化对辅助线本身的认识：

可以在形内，也可以在形外；可以是一条，也可以是多条

人教版八年纪上册第十一章介绍了三角形全等的相关知识。在作业中，不难发现有一类问题是学生感觉比较困难的，即关于三角形中不等关系的证明。这类问题往往需要适当添加辅助线，构造全等三角形，将某些线段进行“等量代换”，最后结合三角形两边之和大于第三边，两边之差小于第三边的性质得出结论。这里，问题的难点在于如何添加辅助线？就此，笔者在研读《课标》的基础上，结合教学实践，对怎样指导学生添加辅助线提出以下几点意见：

1、积累平面图形位置关系变换的常见方法：

折叠、平移、旋转、翻转、对称、拼接 ……