12．(2008·江苏，22)如图，设动点P在棱长为1的正方形ABCD－A₁B₁C₁D₁的对角线BD₁上，记＝λ.当∠APC为钝角时，求λ的取值范围．

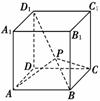
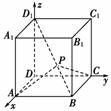
[解]　由题设可知，以、、为单位正交基底，建立如图所示的空间直角坐标系Dxyz，则有A(1,0,0)，B(1,1,0)，C(0,1,0)，D₁(0,0,1)．

由＝(1,1，－1)得＝λ＝(λ，λ，－λ)，

所以＝+＝(－λ，－λ，λ)+(1,0，－1)

＝(1－λ，－λ，λ－1)，

＝+＝(－λ，－λ，λ)+(0,1，－1)

＝(－λ，1－λ，λ－1)．

显然∠APC不是平角，所以∠APC为钝角等价于

cos∠APC＝cos〈，〉＝＜0，这等价于·＜0，即(1－λ)(－λ)+(－λ)(1－λ)+(λ－1)²＝(λ－1)(3λ－1)＜0，得＜λ＜1.

因此，λ的取值范围为(，1)．

亲爱的同学请写上你的学习心得

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

11．(2008·四川高考题)如右图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD＝∠FAB＝90°，BC綊AD，BE綊AF.

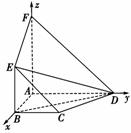
证明：C、D、F、E四点共面．

[证明]　∵面ABEF⊥面ABCD，

AF⊥AB＝90°，

∴AF⊥面ABCD.

∴以A为原点，以AB，AD，AF所在直线为x轴，y轴，z轴，建立空间直角坐标系A?xyz.

不妨设AB＝a，AD＝2b，AF＝2c，则A(0,0,0)，B(a,0,0)，C(a，b,0)，D(0,2b,0)，E(a,0，c)，F(0,0,2c)．

∴＝(0，－2b,2c)，＝(0，－b，c)，

∴＝2，∴∥，

∵E∉DF，∴DF∥CE，

∴C、D、E、F四点共面．

10．(2009·安徽，11)在空间直角坐标系中，已知点A(1,0,2)，B(1，－3,1)，点M在y轴上，且M到A与到B的距离相等，则M的坐标是________．

[解析]　设M(0，y,0)，由|MA|＝|MB|得

(1－0)²+(0－y)²+(2－0)²

＝(1－0)²+(－3－y)²+(1－0)²，

解得y＝－1.

∴M(0，－1,0)．

[答案]　(0，－1,0)

9．已知空间三点A(－2,0,2)，B(－1,1,2)，C(－3,0,4)，设a＝，b＝，若向量ka+b与ka－2b互相垂直，则k的值为________．

[答案]　－或2

8．(2007·安徽)在正四面体O－ABC中，＝a，＝b，＝c，D为BC的中点，E为AD的中点，则＝________(用a，b，c表示)．

[答案]　a+b+c

7．已知三点A(1,0,0)，B(3,1,1)，C(2,0,1)，则

(1)与的夹角等于________；

(2)在方向上的投影等于________．

[解析]　＝(1,1,0)，＝(－1,0，－1)，

(1)cos〈，〉＝＝＝－，

∴〈，〉＝；

(2)在方向上的投影＝＝＝－.

[答案]　(1)　(2)－

6．如图，空间四边形OABC中，＝a，＝b，＝c，点M在OA上，且OM＝2MA，N为BC中点，则等于

(　)

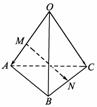
A.a－b+c

B．－a+b+c

C.a+b－c

D.a+b－c

[解析]　 ＝－＝(+)－

＝(b+c)－a＝－a+b+c.

故选B.

[答案]　B

5．已知空间四边形ABCD每边及对角线长均为，E，F，G分别是AB，AD，DC的中点，则·等于

(　)

A.　 　　　　　　　　　　　　　　　　　　 　　　 B．1

C.　 　　　　　　　　　　　　　　　　　 　　　 D.

[解析]　由于ABCD为正四面体，E、F、G为中点，因此△EFG为等腰直角三角形，所以·＝||·||cos45°＝1××＝.故选A.

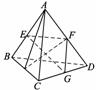
[答案]　A