3.“初唐四杰”是　　　　　 、　　　　 、　　　　 、　　　　 。(2分)

2.在《逍遥游》一文中，“逍遥”的意思是________________。作者认为，要达到“逍遥游”的境界，就得做到_________、_________、_________。(2分)

1．看拼音，写汉字。(4分)

bū(　　 )慢　 舟遥遥以轻yáng(　 )　 睇miǎn(　　 )　　 gě(　　 )舰迷津

yáo(　　 )tiǎo(　　 )　　 liǎo(　　 )水尽　　　 门衰zhuò (　　 )薄

22.(本小题满分14分)

定义在(－1，1)上的函数f(x)满足：对任意x、y∈(－1，1)都有f(x)+f(y)=f()．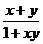

(1)求证：函数f(x)是奇函数；

(2)如果当x∈(－1，0)时，有f(x)＞0，求证：f(x)在(－1，1)上是单调递减函数；

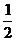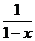(3)在(2)的条件下解不等式：f(x+)+f()＞0．

21.(本小题满分12分)

已知动点P与双曲线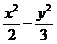=1的两个焦点F₁、F₂的距离之和为定值，且cosF₁PF₂的最小值为－．

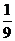(1)求动点P的轨迹方程；

(2)若已知D(0，3)，M、N在动点P的轨迹上，且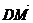=λ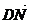，求实数λ的取值范围．

20.(本小题满分12分)

因居民住房拆迁的需要，准备在某小区建造总面积为40000 m²完全相同的住房若干栋.已知面积为M的一栋房子，其造价是由地面部分造价和基础部分造价组成，地面部分的造价与M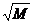成正比，基础部分的造价与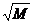成正比.据统计，一栋面积为1600 m²的住房造价是176.8万元，其中地面部分的费用是基础部分的36%，试确定:建造多少栋房子，可使总费用最少？并求出总费用.

18.(本小题满分12分)

如图，在多面体ABCDE中，AE⊥面ABC，BD∥AE，且AC=AB=BC=BD=2，AE=1，F为CD中点．

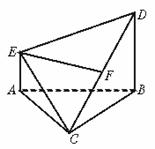
(1)求证：EF⊥面BCD；

(2)求多面体ABCDE的体积；

(3)求面CDE与面ABDE所成的二面角的余弦值．

19_.(本小题满分12分)

已知递增等比数列{a_n}满足a₂+a₃+a₄=28，且a₃+2是a₂、a₄的等差中项.

(1)求{a_n}的通项公式a_n；

(2)若b_n=a_nlog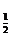a_n，S_n=b₁+b₂+…+b_n，求S_n+n·2ⁿ⁺¹＞30成立的n的最小值.

17.(本小题满分12分)

设e₁，e₂是两个垂直的单位向量，且a=－(2e₁+e₂)，b=e₁－λe₂.

(1)若a∥b，求λ的值；

(2)若a⊥b，求λ的值.

16.已知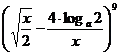的展开式中x³的系数为，则实数a的值为_________.

15. 袋中有3个5分硬币，3个2分硬币和4个1分硬币，从中任取3个，总数超过8分的概率是_________.