
9.有一瓶混有酵母菌的葡萄糖培养液,当通入不同浓度的氧气时,其产生的C2H5OH和CO2的量如下表所示。通过对表中数据分析可得出的结论是( )
|
氧浓度(%) |
a |
b |
c |
d |
|
产生CO2的量 |
9mol |
12.5 mol |
15 mol |
30mol |
|
产生酒精的量 |
9mol |
6.5 mol |
6 mol |
0 mol |
A.a浓度时酵母菌有氧呼吸速率等于无氧呼吸速率
B.b浓度时酵母菌有氧呼吸速率大于无氧呼吸速率
C.c浓度时有50%的葡萄糖用于酵母菌的酒精发酵
D.d浓度时酵母菌只进行有氧呼吸未进行无氧呼吸
8.在一个普通的锥形瓶中,加入含有酵母菌的葡萄糖溶液,如图所示,则下列有关坐标中,正确的是( )
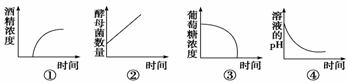

A.①②③ B.①③④ C.②③④ D.①②④
7.下图表示过氧化氢被分解的曲线,可说明酶具有( )

①专一性 ②高效性 ③催化特性(降低活化能) ④在温和条件下进行
A.①④ B.②③ C.①② D.③④
6.将萤火虫腹部末端的发光器切下,干燥后研成粉末。将粉末装入试管,滴加蒸馏水,使之混合,则有淡黄色荧光出现,2 min后,荧光消失了。接着若在试管中滴加葡萄糖溶液,荧光不能恢复,如果滴一点ATP溶液,荧光将恢复。下列相关叙述中,错误的是( )
A.滴入蒸馏水发出荧光,是由于试管内有荧光物质和ATP
B.荧光消失是由于ATP水解酶的活性降低所致
C.滴加ATP溶液,荧光恢复,说明萤火虫发出荧光需要消耗ATP
D.滴加葡萄糖溶液,荧光不能恢复,说明葡萄糖不是直接能源
5.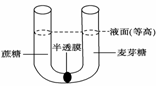 如图所示U型管中间被一种能允许水分子通过而单糖和二糖不能透过的半透膜隔开,现在两侧分别加入0.1 mol/L的蔗糖溶液和麦芽糖溶液,一段时间后左右两侧液面高度变化是怎样的?若向U形管右侧加入某种微量物质(不影响溶液浓度),右侧液面高度上升,那么加入的这种微量物质最可能是 ( )
如图所示U型管中间被一种能允许水分子通过而单糖和二糖不能透过的半透膜隔开,现在两侧分别加入0.1 mol/L的蔗糖溶液和麦芽糖溶液,一段时间后左右两侧液面高度变化是怎样的?若向U形管右侧加入某种微量物质(不影响溶液浓度),右侧液面高度上升,那么加入的这种微量物质最可能是 ( )
A.右侧液面高度下降;胰岛素 B.右侧液面高度下降;蔗糖酶
C.两侧液面高度不变;麦芽糖酶 D.两侧液面高度不变;蒸馏水
4.如图4-A-2所示,烧杯内装有蒸馏水,下部封有半透膜的长颈漏斗内装有淀粉和食盐溶液,漏斗颈内液面与烧杯内蒸馏水的液面相同。过一段时间后用碘水和硝酸银溶液分别检测蒸馏水中的物质。整个实验过程中所观察到的现象是( )
①漏斗颈内液面下降 ②漏斗颈内液面上升 ③烧杯内的液体遇硝酸银溶液有白色沉淀生成 ④烧杯内的液体遇碘水变蓝
A.② B.②③ C.③④ D.①④
2.如图表示各种膜的组成成分含量: 图中不能说明的是( )
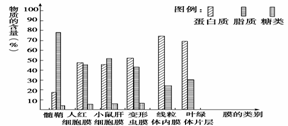
A.构成细胞膜的主要成分是蛋白质和脂质 B.膜中的脂质和蛋白质含量的变化与膜的功能有关
C.膜的功能越简单,所含蛋白质的数量越少 D.膜的功能越复杂,所含糖类的种类和数量越多
3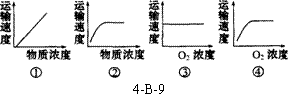 .科学家在研究细胞膜运输物质时发现有下列四种关系,分别用下图4-B-9中四条曲线表示,在研究具体的物质x时,发现与曲线②和④相符。试问:细胞膜运输物质X的方式是( )
.科学家在研究细胞膜运输物质时发现有下列四种关系,分别用下图4-B-9中四条曲线表示,在研究具体的物质x时,发现与曲线②和④相符。试问:细胞膜运输物质X的方式是( )
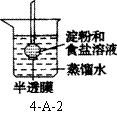 A.自由扩散 B.协助扩散 C.主动运输 D.胞吐
A.自由扩散 B.协助扩散 C.主动运输 D.胞吐
1.氨基酸的R基团不同,氨基酸种类就不同,现有a,b,c三个不同氨基酸缩合,可能形成几种三肽 ( )
A.6 种 B.9种 C.3种 D.1种
15.(10分)解:当a=0时,不等式的解为x>1;---------------1分
当a≠0时,分解因式a(x-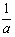 )(x-1)<0--------------2分
)(x-1)<0--------------2分
当a<0时,原不等式等价于(x-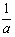 )(x-1)>0,
)(x-1)>0,
不等式的解为x>1或x<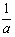 ;--------------4分
;--------------4分
当0<a<1时,1<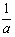 ,不等式的解为1<x<
,不等式的解为1<x<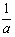 ;-------6分
;-------6分
当a>1时,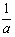 <1,不等式的解为
<1,不等式的解为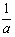 <x<1;----------8分
<x<1;----------8分
当a=1时,不等式的解为φ。-----------10分
16(10分)证明:(1)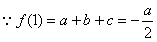

又

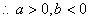 ……………………2分
……………………2分
又2c=-3a-2b 由3a>2c>2b ∴3a>-3a-2b>2b
∵a>0  ………………………………………………4分
………………………………………………4分
(2)∵f(0)=c,f(2)=4a+2b+c=a-c………………………………6分
①当c>0时,∵a>0,∴f(0)=c>0且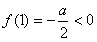
∴函数f(x)在区间(0,1)内至少有一个零点……………………8分
②当c≤0时,∵a>0 
∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点…………………………10分
17(12分)解:①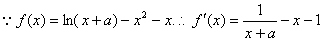
又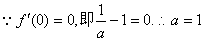 …………4分
…………4分
由
设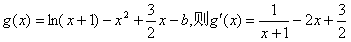
即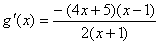

 …………12分
…………12分
18(12分)解:(1) 的定义域为
的定义域为 -----------1分
-----------1分  …………2分
…………2分
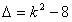
①当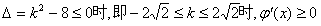 …………3分
…………3分
②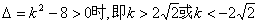 时
时
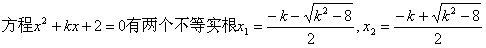
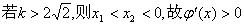 …………4分
…………4分

 …………5分
…………5分

单调递减区间为
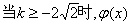 的单调递增区间(0,+
的单调递增区间(0,+ ) …………6分
) …………6分
(2) …………7分
…………7分
 …………8分
…………8分
则 …………9分
…………9分
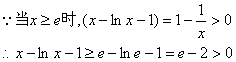
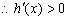 …………10分
…………10分
 …………11分
…………11分
 …………12分
…………12分
另解:
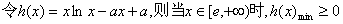 …………7分
…………7分
 …………8分
…………8分

 单增 …………9分
单增 …………9分
①当

 …………11分
…………11分
②当

 不成立 …………12分
不成立 …………12分
综上所述
3、解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com