
3. 由2(log2x)2-7log2x+3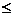 0解得
0解得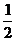
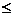 log2x
log2x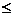 3。∵f(x)=log2
3。∵f(x)=log2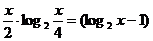 (log2x-2)=(log2x-
(log2x-2)=(log2x-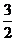 )2-
)2-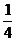 ,∴当log2x=
,∴当log2x=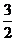 时,f(x)取得最小值-
时,f(x)取得最小值-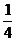 ;当log2x=3时,f(x)取得最大值2。
;当log2x=3时,f(x)取得最大值2。
3.(1)f(x)=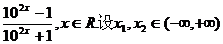 ,
,
,且x1<x2,f(x1)-f(x2)=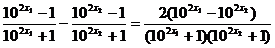 <0,(∵102x1
<0,(∵102x1 <102x2)∴f(x)为增函数。
<102x2)∴f(x)为增函数。
(2)由y=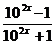 得102x=
得102x=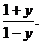
∵102x>0,
∴-1<y<1,又x=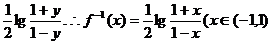 )。
)。
2. 已知f(x)=lg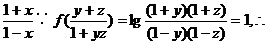
 ①,又∵f(
①,又∵f(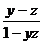 )=lg
)=lg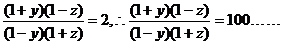 ②,
②,
①②联立解得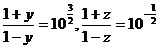 ,∴f(y)=
,∴f(y)=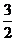 ,f(z)=-
,f(z)=-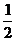 。
。
1. f(x)-g(x)=logx3x-logx4=logx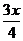 .当0<x<1时,f(x)>g(x);当x=
.当0<x<1时,f(x)>g(x);当x=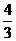 时,f(x)=g(x);当1<x<
时,f(x)=g(x);当1<x<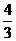 时,f(x)<g(x);当x>
时,f(x)<g(x);当x>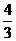 时,f(x)>g(x)。
时,f(x)>g(x)。
10.-log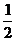 (-x)
(-x)
已知f(x)=(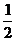 )x,则f-1(x)=log
)x,则f-1(x)=log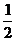 x,∴当x>0时,g(x)=log
x,∴当x>0时,g(x)=log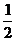 x,当x<0时,-x>0, ∴g(-x)
x,当x<0时,-x>0, ∴g(-x)
=log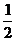 (-x),又∵g(x)是奇函数,∴
g(x)=-log
(-x),又∵g(x)是奇函数,∴
g(x)=-log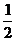 (-x)(x<0)
(-x)(x<0)
9.y=lg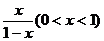 y=
y=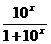 ,则10x=
,则10x=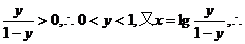 反函数为y=lg
反函数为y=lg 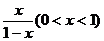
8.-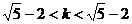
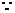 y=lg[x2+(k+2)x+
y=lg[x2+(k+2)x+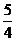 ]的定义域为R,∴ x2+(k+2)x+
]的定义域为R,∴ x2+(k+2)x+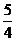 >0恒成立,则
>0恒成立,则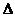 (k+2)2-5<0,即k2+4k-1<0,由此解得-
(k+2)2-5<0,即k2+4k-1<0,由此解得-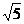 -2<k<
-2<k<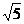 -2
-2
7.-1
6.(-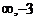 ) ∵x2-6x+17=(x-3)2+8
) ∵x2-6x+17=(x-3)2+8 ,又y=log
,又y=log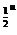 单调递减,∴ y
单调递减,∴ y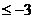
5.f(3)<f(4)
设y=log0.5u,u=-x2+4x+5,由-x2+4x+5>0解得-1<x<5。又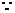 u=-x2+4x+5=-(x-2)2+9,∴ 当x
u=-x2+4x+5=-(x-2)2+9,∴ 当x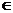 (-1,2)时,y=log0.5(-x2+4x+5)单调递减;当x
(-1,2)时,y=log0.5(-x2+4x+5)单调递减;当x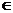 [2,5]时,y=log0.5(-x2+4x+5)单调递减,∴f(3)<f(4)
[2,5]时,y=log0.5(-x2+4x+5)单调递减,∴f(3)<f(4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com