22.(本小题满分14分)

设函数f(x)=x²+2bx+c(c＜b＜1)，f(1)=0，且方程f(x)+1=0有实根．

(1)证明：－3＜c≤－1，且b≥0；

(2)若m 是方程f(x)+1=0的一个实根，判断f(m－4)的正负，并加以证明．

21.(本小题满分12分)

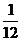已知点B₁(1，y₁)，B₂(2，y₂)，…，B_n(n，y_n)，…(n∈N^*)顺次为直线y=x+上的点，点A₁(x₁，0)，A₂(x₂，0)，…，A_n(x_n，0)，…顺次为x轴上的点，其中x₁=a(0＜a＜1).对于任意n∈N^*，点A_n，B_n，A_n+1构成以B_n为顶点的等腰三角形．

(1)求数列{y_n}的通项公式，并证明它为等差数列；

(2)求证：x_n+2－x_n是常数，并求数列{x_n}的通项公式；

(3)上述等腰△A_nB_nA_n+1中是否可能存在直角三角形，若可能，求出此时a的值；若不可能，请说明理由．

20.(本小题满分12分)

如图，已知椭圆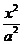+y²=1(a＞1)，直线l过点A(－a，0)和点B(a，ta)(t＞0)交椭圆于M，直线MO交椭圆于N．

(1)用a，t表示△AMN的面积S；

(2)若t∈［1，2］，a为定值，求S的最大值.

18.(本小题满分12分)

甲、乙两人独立解出某一道数学题的概率相同，已知该题被甲或乙解出的概率为　　 0.36，求：

(1)甲独立解出该题的概率；

(2)甲、乙中有且只有一个解出该题的概率．

19_.(本小题满分12分)

如图，已知斜三棱柱ABC－A₁B₁C₁，∠BCA＝90°，AC＝BC＝a，A₁在底面ABC上的射影恰为AC的中点D，又A₁B⊥AC₁．

(1)求证：BC⊥平面ACC₁A₁；

(2)求AA₁与平面ABC所成的角；

(3)求二面角B－AA₁－C的正切值．

17.(本小题满分12分)

设向量a=(cos23°，cos67°)，b=(cos68°，cos22°)，u=a+tb(t∈R).

(1)求：a·b；

(2)求u的模的最小值．

16.已知两点M(－5，0)，N(5，0)，给出下列直线方程:①5x－3y=0；②5x－3y+30=0；　　　 ③x－y=0；④4x－y+5=0．在直线上存在点P满足|MP|＝|NP|+6的所有直线方程的序号是__________．

15.已知x=－2与x=4是函数f(x)=x³+ax²+bx的两个极值点，则a=__________，?b=___________?.

14.正方形ABCD中，E、F分别是AB、CD的中点，沿EF将正方形折成60°的二面角，则异面直线BF与DE所成角的余弦是 __________．

13.若(x²+)ⁿ的展开式中，只有第四项的系数最大，那么这个展开式的常数项是 __________．

12.函数f(x)=log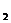|x|，g(x)=－x²+2，则f(x)·g(x)的图象只可能是

第Ⅱ卷　 (非选择题　 共90分)