在成语中有一些成语有运用的对象，如“炙手可热”只能用于权势，“美仑美奂”只形容建筑，“罄竹难书”只形容罪恶，“不瘟不火”只形容戏剧表演，“匪夷所思”只形容言谈举止，运用时要十分注意，否则就会出错，如“这副画炙手可热。”又如“他把这理论批驳得遍体鳞伤。”“遍体鳞伤”只能用于人，这里应用“体无完肤”。这一类的成语还有“不胫而走”、“不翼而飞”、“巧夺天工”、“青梅竹马”等。

　成语作为一种固定短语，具有稳定性，但也不是一层不变的，要注意其感情色彩，以便正确运用。如“明目张胆”，古代形容不畏权势，敢作敢为，有胆略，有气概，含褒义，到现代，指人公开干坏事，成了贬义词；又如“为了救活这家濒临倒闭的工厂，新上任的领导，积极开展市场调查，狠抓产品质量和开发，真可谓处心积虑。”“处心积虑”是存心已久，费尽心思，也指千方百计地谋算，是贬义词，用在这里感情色彩不当；还有如“趋之若骛”意思是像鸭子一样成群跑过去，用来比喻很多人争着赶去，含贬义。这一类的成语还有明哲保身、好为人师等。

22、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (本小题满分14分) 对函数Φ(x)，定义f_k(x)＝Φ(x－mk)+nk(其中x∈(mk，m+mk]，k∈Z，m＞0，n＞0，且m、n为常数)为Φ(x)的第k阶阶梯函数，m叫做阶宽，n叫做阶高，已知阶宽为2，阶高为3. (1)当Φ(x)＝2^x时 　 ①求f₀(x)和f_k(x)的解析式； 　 ②求证：Φ(x)的各阶阶梯函数图象的最高点共线； (2)若Φ(x)＝x²，则是否存在正整数k，使得不等式f_k(x)＜(1－3k)x+4k²+3k－1有解？若存在，求出k的值；若不存在，请说明理由.

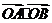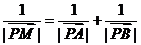21、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (本小题满分12分) 设直线l(斜率存在)交抛物线y²＝2px(p＞0，且p是常数)于两个不同点A(x₁，y₁)，B(x₂，y₂)，O为坐标原点，且满足＝x₁x₂+2(y₁+y₂). (1)求证：直线l过定点； (2)设(1)中的定点为P，若点M在射线PA上，满足，求点M的轨迹方程.

20、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (本小题满分12分) 已知等差数列{a_n²}中，首项a₁²＝1，公差d＝1，a_n＞0，n∈N^*. (1)求数列{a_n}的通项公式； (2)设b_n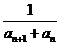＝，数列{b_n}的前n项和为T_n； 　 ①求T₁₂₀； 　 ②求证：当n＞3时，2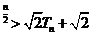

19、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (本小题满分12分) 如图，在四边形ABCD中，AC⊥BD，垂足为O，PO⊥平面ABCD，AO＝BO＝DO＝1，CO＝PO＝2，E是线段PA上的点，AE∶AP＝1∶3. (1)求证：OE∥平面PBC； (2)求二面角D－PB－C的大小.

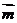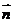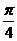18、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (本小题满分12分) 已知向量＝(sin2x，cos2x)，＝(cos，sin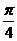)，函数f(x)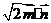＝+2a(其中a为实常数) (1)求函数f(x)的最小正周期； (2)若x∈[0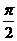，]时，函数f(x)的最小值为－2，求a的值.

17、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (本小题满分12分) 某公司购买了一博览会门票10张，其中甲类票4张，乙类票6张，现从这10张票中任取3张奖励一名员工. (1)求该员工得到甲类票2张，乙类票1张的概率； (2)求该员工得到甲类票张数多于乙类票张数的概率，

16、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 已知圆C：x²+y²+2x+Ey+F＝0(E、F∈R)，有以下命题：①E＝－4，F＝4是曲线C表示圆的充分非必要条件；②若曲线C与x轴交于两个不同点A(x₁，0)，B(x₂，0)，且x₁、x₂∈[－2，1)，则0≤F≤1；③若曲线C与x轴交于两个不同点A(x₁，0)，B(x₂，0)，且x₁、x₂∈[－2，1)，O为坐标原点，则|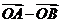|的最大值为2；④若E＝2F，则曲线C表示圆，且该圆面积的最大值为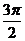. 其中所有正确命题的序号是_______________________.

15、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 已知实数x、y满足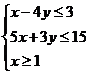，则2x+y的最大值为__________________.