1、 已知∆ABC中，BC长为6，周长为16，那么顶点A在怎样的曲线上运动？

4．数学应用

例1、试用适当的方法作出以两个定点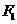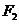，为焦点的一个椭圆。

思考：在椭圆的定义中，如果这个常数小于或等于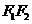，动点的轨迹又如何呢？

例2、已知∆ABC中，B(-3，0)，C(3，0)，且AB，BC，AC成等差数列。

(1)求证：点A在一个椭圆上运动；

(2)写出这个椭圆的焦点坐标。

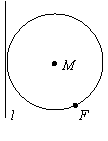例3、已知定点F和定直线l，F不在直线l上，动圆M过F且与直线l相切，求证：圆心M的轨迹是一条抛物线。

变题：已知定点F和定圆C，F在圆C外，动圆M过F且与圆C相切，探究动圆的圆心M的轨迹是何曲线？(提示：相切须考虑外切和内切)

课堂练习

2．建构数学

(1)圆锥曲线的定义

椭圆：_____________________________，______________叫做椭圆的焦点，______________ 叫做椭圆的焦距。

双曲线：___________________________，___________________叫做双曲线的焦点，___________________叫做双曲线的焦距。

抛物线：___________________________，___________________叫做抛物线的焦点，___________________叫做抛物线的准线。

(2)圆锥曲线的定义式

上面的三个结论我们都可以用数学表达式来体现：设平面内的动点为M。

椭圆：动点M满足的式子： _____________(__________)

双曲线：动点M满足的式子：_____________(_________)

抛物线：动点M满足的式子：__________我们可利用上面的三条关系式来判断动点M的轨迹是什么！

1．问题情境

我们知道，用一个平面截一个圆锥面，当平面经过圆锥面的顶点时，可得到两条相交直线，当平面与圆锥面的轴垂直时，截得的图形是一个圆，试改变平面的位置，观察截得的图形的变化情况。用平面去截圆锥面能得到哪些曲线？

(1)　　　　 (2)　　　　　 (3)

2．通过用平面截圆锥面,感受、了解双曲线的定义。能用数学符号或自然语言描述双曲线的定义。

1.通过用平面截圆锥面,经历从具体情境中抽象出椭圆、抛物线模型的过程，掌握它们的定义，并能用数学符号或自然语言的描述。

21.

20.

19.

18。(1)①　　　　　 　　　　　　　　， 　　　　　　　　　　　　　　　

　　　　 ②　　　　　　 　　　　　　　　

　　　　 ③　 　　　　　　　　　　　　， 　　　　　　　　　　　　　

　　　 (2)　　　　　　 　

四 计算题(共26分)