1、 已知∆ABC中，BC长为6，周长为16，那么顶点A在怎样的曲线上运动？

4．数学应用

例1、试用适当的方法作出以两个定点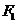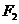，为焦点的一个椭圆。

思考：在椭圆的定义中，如果这个常数小于或等于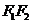，动点的轨迹又如何呢？

例2、已知∆ABC中，B(-3，0)，C(3，0)，且AB，BC，AC成等差数列。

(1)求证：点A在一个椭圆上运动； (2)写出这个椭圆的焦点坐标。

略解：由AB，BC，AC成等差数列，可得2BC=AB+AC,即AB+AC=12>BC,由椭圆的定义可得点A在一个椭圆上运动，且以B、C为焦点。

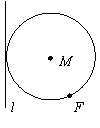例3、已知定点F和定直线l，F不在直线l上，动圆M过F且与直线l相切，求证：圆心M的轨迹是一条抛物线。

分析：欲证明轨迹为抛物线只需抓住抛物线的定义即可。

变题：已知定点F和定圆C，F在圆C外，动圆M过F且与圆C相切，

探究动圆的圆心M的轨迹是何曲线？

提示：相切须考虑外切和内切。

课堂练习

3．建构数学

(1)圆锥曲线的定义

椭圆：平面内到两定点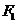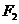，的距离和等于常数(大于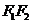)的点的轨迹叫做椭圆，两个定点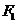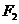，叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。

对于第二种情形，平面与圆锥曲线的截线由两支曲线构成。(类比椭圆的定义)

双曲线：平面内到两定点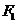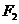，的距离的差的绝对值等于常数(小于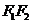)的点的轨迹叫做双曲线，两个定点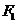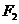，叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距。

对于第三种情形，平面与圆锥曲线的截线是一条曲线构成。

抛物线：平面内到一个定点F和一条定直线L(F不在L上)的距离相等的点轨迹叫做抛物线，定点叫做抛物线的焦点，定直线L叫做抛物线的准线。

(2)圆锥曲线的定义式

上面的三个结论我们都可以用数学表达式来体现：设平面内的动点为M。

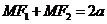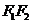椭圆：动点M满足的式子：(2a>的常数)

双曲线：动点M满足的式子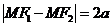：(0<2a<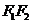的常数)

抛物线：动点M满足的式子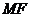：=d(d为动点M到直线L的距离)

我们可利用上面的三条关系式来判断动点M的轨迹是什么！

2．学生活动

学生讨论上述问题，通过观察,可以得到以下三种不同的曲线：

对于Dandelin双球理论只要让学生感知、认同即可。

1．问题情境

我们知道，用一个平面截一个圆锥面，当平面经过圆锥面的顶点时，可得到两条相交直线，当平面与圆锥面的轴垂直时，截得的图形是一个圆，试改变平面的位置，观察截得的图形的变化情况。提出问题：用平面去截圆锥面能得到哪些曲线？

2．通过用平面截圆锥面,感受、了解双曲线的定义。能用数学符号或自然语言描述双曲线的定义。

教学重点、难点

重点：椭圆、抛物线、双曲线的定义。

难点：用数学符号或自然语言描述三种曲线的定义

内容分析

本节课教材利用平面对圆锥面的不同截法，产生三种不同的圆锥曲线，得出椭圆、双曲线和抛物线的概念。这样既使学生经历概念的形成过程，更有利于从整体上认识三种圆锥曲线的内在关系。根据问题的难易度及学生的认知水平，要求学生掌握椭圆、抛物线的定义，对双曲线只要求了解其定义。这是建立在学生的最近发展区上的形式化的过程，有利于培养学生的数学化能力，提高数学素养。

学法指导

教学中向学生展示平面截圆锥面得到椭圆的过程，使学生加深对圆锥曲线的理解。对用Dandelin双球发现椭圆的特性(由此形成椭圆的定义)，可直接给出放进双球后的图形，再引导学生发现“到两切点距离之和为定值”的特性，这一内容让学生感知、认同即可，不必对探究、推理过程作过多研究。

教学过程设计

1.通过用平面截圆锥面,经历从具体情境中抽象出椭圆、抛物线模型的过程，掌握它们的定义，并能用数学符号或自然语言的描述。

6．作业布置

(1)教学与测试、测试与反馈对应练习

(2)预习椭圆的标准方程

通过预习我已经掌握了

我还有要交流的问题是

我的建议

5．回顾小结

(1)三种圆锥曲线的定义

(2)三种圆锥曲线的定义式

2、 设Q是圆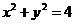上的动点，另有点A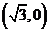，线段AQ的垂直平分线l交半径OQ于点P，当Q点在圆周上运动时，则点P的轨迹是何曲线？